幾何

過圓上一點求切線（二）（Finding the tangent line through a point on a circle Ⅱ）
國立臺灣師範大學數學所博士班黃俊瑋

連結：過圓上一點求切線（一）

前文〈過圓上一點求切線（一）〉裡，介紹了此問題的公式解以及另外兩類求切線方法。本文繼續介紹其它方法，其中包含了兩種與微分相關的方法。在此先重述一次原問題：

已知坐標平面上一圓之方程式為 \({(x – 1)^2} + {(y – 2)^2} = 5\)，
求過此圓上一點 \(P(3,1)\) 的切線方程式。

方法3圓心到切線距離等於半徑 

先利用點斜式可假設過 \(P(3,1)\) 之切線方程式為：\(y-1=m(x-3)\)。

又如圖一所示，圓心到切線距離等於圓之半徑（\(d(O,L) = r\)），利用此關係以及點到直線距離公式可得：

\(\displaystyle\frac{{|m – 2 – 3m + 1|}}{{\sqrt {{m^2} + 1} }} = \sqrt 5\)

此時，兩邊平方並進一步整理解之得 \(m=2\)。則所求切線為 \(y-1=2(x-3)\)。

過圓上一點求切線（一）（Finding the tangent line through a point on a circle Ⅰ）
國立臺灣師範大學數學所博士班黃俊瑋

高二上圓與直線相關單元裡，除了介紹平面上的圓與直線的方程式之外，也進一步利用方程式討論了圓與直線的關係。其中，當直線與圓相切時，又衍生出三類常見求切線問題：1.過圓上一點求切線、2.過圓外一點求切線，以及3.求已知斜率之切線。

本文主要聚焦在第一類過圓上一點求切線問題上，一方面提供多類解法，並說明該解法能否推廣用於其它兩類問題，以及能否推廣至拋物線、橢圓與雙曲線相關求切線問題上（現今高中課程有關三類圓錐曲線的求切線問題已刪除，因此，這部份筆者僅略述之）。

橢圓平行弦中點共線問題
（Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse）
臺北市立和平高中黃俊瑋教師

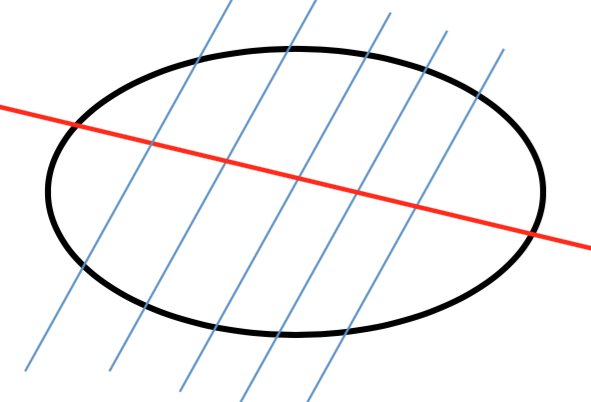
高中圓錐曲線單元裡，一個常見的延伸問題如下：在橢圓  \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 內所有斜率為 \(2\) 的平行弦，已知這些弦的中點共線，請問其所在直線方程式為何（參見圖一）？

換言之，本問題相當於：已知直線 \(y = 2x + k\) 與 \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 相截於兩點 \(A,B\)，當參數 \(k\) 變動時，求 \(A\) 與 \(B\) 之中點 \(M(x,y)\) 的軌跡所在直線方程式。

圖一\(~~~\)斜率為 \(m\) 的平行弦中點軌跡所在圖形

平面上點到直線距離（三） (The distance from a point to a line in the plane Ⅲ）
臺北市立和平高中教師黃俊瑋

連結：平面上點到直線距離（二）

本文承〈平面上點到直線距離(一)〉與〈平面上點到直線距離(二)，繼續提出三類平面上點到直線距離的解法以及相關討論與連結。而本文中的各類解法，主要在直線上任取一點或兩點，造出新向量，所延伸出的方法。

方法5：在直線上任取一點，再利用平行與垂直性質

本類方法主要是引入直線上的一點後，充份利用直線的法向量與方向向量，輔以平行與垂直相關性質與關係，求得投影點與距離。

方法5-1：在直線上任取一點，再利用平行與垂直相關性質

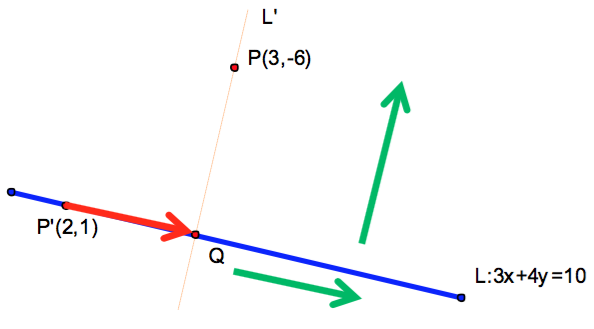
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\) ，
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點，\(\vec{P’Q}\) 與直線之方向向量平行，可設為 \(\vec{P’Q}=t(4,-3)\)。

接下來，可發展出兩種方法，分別利用直線的法向量或方向向量，搭配平行與垂直關係進行解題：

5-1-1

則 \(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 平行直線 \(L:3x+4y=10\) 的法向量
分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\)，可得 \(4(1-4t)=3(-7+3t)\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

5-1-2

\(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 垂直直線 \(L:3x+4y=10\) 的方向向量
內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求(參考圖一所示)。

圖一 在直線上任取一點，再利用平行與垂直性質(一)

平面上點到直線距離（一） (The distance from a point to a line in the plane Ⅰ）
臺北市立和平高中教師黃俊瑋

求平面上一點 \(P(x_0,y_0)\) 點到直線 \(L:ax+by+c=0\) 距離問題，是高中課程中重要而基本的問題，此問題出現在平面向量單元裡，課程中並且提供了公式解：

\(\displaystyle d(P,L)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)

而這個公式 除了可用以推導出平面上兩平行直線之距雄公式之外，亦可推廣至空間中，求一點 \(P(x_0,y_0,z_0)\) 點到平面 \(E:ax+by+cz=0\) 距離問題。

儘管「代公式」的方式簡便而快速，但事實上，除了公式解之外，尚存在許多不同的解法，這些解法分屬於高中坐標幾何、向量幾何與三角學等課程範疇，若不考慮各解法背後的邏輯關係，在學完相關單元後，可以由此問題出發，進行一題多解，將坐標幾何、向量幾何相關單元中的重要概念，作一連結，而當中的許多方法與想法，亦可進一步用於空間中點、線、面相關距離問題。以下，我們以實際問題為例，在本文以及〈平面上點到直線距離(二)〉、〈平面上點到直線距離(三)〉等文裡，提供公式解之外，共七大類，近20種解法，除了討論各類解法所涉先備知識，以及這些方法與空間中相關問題之間的連結。

空間向量的外積及幾何意義 ( The cross product and its geometric interpretation )
臺北市立和平高中黃俊瑋教師

現今高二下有關空間向量的教材提到，若 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 為空間中的兩向量，則定義 \(\overrightarrow a\) 與 \(\overrightarrow b\) 兩向量之外積

\(\overrightarrow a\times \overrightarrow b=(\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|)\)。

另一方面，空間中 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 兩向量所張成的平行四邊形面積為：

\(A = \sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}}\)

眼尖的讀者，不難發現  \(\overrightarrow a\times\overrightarrow b\) 之長恰為此平行四邊形之面積值，即 \(A = \left| {\overrightarrow a\times\overrightarrow b }\right|\)。