線性代數

行列式的應用（Applications of Determinant）
國立臺南第一高級中學林倉億老師

連結：行列式的性質

以下介紹行列式在高中數學中主要的應用：

1. 表示平面上三角形的面積
   \(\vec{OA}=(a_1,b_1)\)、\(\vec{OB}=(a_2,b_2)\)，則 \(\Delta OAB\) 面積 \(= \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\)
   （\(\frac{1}{2}\) 乘以 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\) 的絕對值）。
   【證明】：
   由三角形面積公式 \(\Delta OAB = \frac{1}{2}\sqrt {{{\left| {\vec{OA}} \right|}^2}{{\left| {\vec{OB}} \right|}^2} – {{\left( {\vec{OA} \cdot\vec{OB}} \right)}^2}}\)
   可得
   \(\begin{array}{ll}\Delta OAB &= \frac{1}{2}\sqrt {({a_{ 1}}^2 + {b_{ 1}}^2)({a_{ 2}}^2 + {b_{ 2}}^2) – {{\left( {{a_{ 1}}{a_{ 2}} + {b_{ 1}}{b_{ 2}}} \right)}^2}} \\&= \frac{1}{2}\sqrt {{a_{ 1}}^2{b_{ 2}}^2 + {a_{ 2}}^2{b_{ 1}}^2 – 2{a_{ 1}}{a_{ 2}}{b_{ 1}}{b_{ 2}}} = \frac{1}{2}\sqrt {{{\left( {{a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}} \right)}^2}} \\&= \frac{1}{2}\sqrt { {{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}^2}} = \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\end{array}\)
2. 表示空間中兩不平行向量的外積
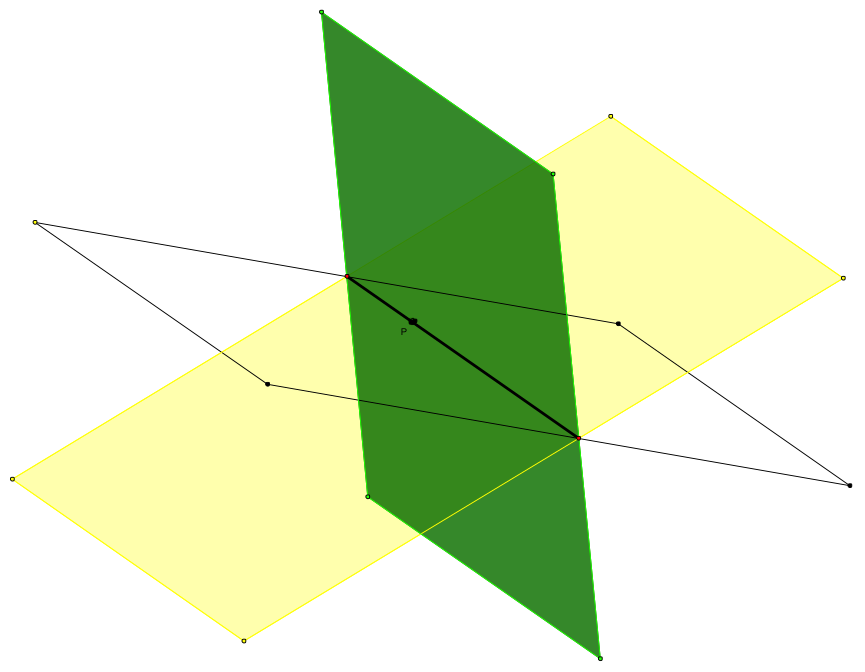
   \(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，則 \(\vec{OA}\) 與 \(\vec{OB}\) 的外積
   可記作 \(\vec{OA}\times\vec{OB}= ( \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| )\) 

行列式的性質（Properties of Determinant）
國立臺南第一高級中學林倉億老師

連結：行列式的定義

在本文中，二階行列式的定義是 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}\)，

三階行列式的定義則是

\(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| = {a_{ 1}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 2}}}&{{c_{ 2}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| – {a_{ 2}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| + {a_{ 3}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}}{c_{ 3}} – {a_{ 1}}{b_{ 3}}{c_{ 2}} + {a_{ 2}}{b_{ 3}}{c_{ 1}} – {a_{ 2}}{b_{ 1}}{c_{ 3}} + {a_{ 3}}{b_{ 1}}{c_{ 2}} – {a_{ 3}}{b_{ 2}}{c_{ 1}}\) 

我們稱直的為行，由左而右依序是第1行、第2行、…；稱橫的為列，由上而下依序是第1列、第2列、…。利用定義，很容易可以推出下列二階與三階行列式性質，證明就略去。

行列式的定義 (Definitions of Determinant)
國立臺南第一高級中學林倉億老師

在高中數學課本中，對於二階與三階行列式，基本上都是直接給出操作型定義：

定義1：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}\\ {{a_{2}}}&{{b_{2}}} \end{array}} \right| = {a_{1}}{b_{2}} – {a_{2}}{b_{1}}\)。

等號的左邊稱為二階行列式，等號的右邊稱為二階行列式的展開式，或稱為二階行列式的值。

定義2：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}&{{c_{1}}}\\ {{a_{2}}}&{{b_{2}}}&{{c_{2}}}\\ {{a_{3}}}&{{b_{3}}}&{{c_{3}}} \end{array}} \right| = {a_{1}}{b_{2}}{c_{3}} + {a_{2}}{b_{3}}{c_{1}} + {a_{3}}{b_{1}}{c_{2}} – {a_{3}}{b_{2}}{c_{1}} – {a_{2}}{b_{1}}{c_{3}} – {a_{1}}{b_{3}}{c_{2}}\)

等號的左邊稱為三階行列式，等號的右邊稱為三階行列式的展開式，或稱為三階行列式的值。

然後再根據定義推導相關的運算性質，最後再介紹它們的應用。定義二其實很難記憶，因此一般教科書都會補充記憶的方法，就是將圖一或圖二中，紅線上的數乘積之和，減去藍線上的數乘積之和。

圖一

圖二

矩陣列運算與基本矩陣
臺北市立和平高中黃俊瑋教師

高中程程中，有關線性方程組與矩陣的相關單元裡，介紹了矩陣的三種基本的列運算：

1. 第 \(i\) 列與第 \(j\) 列互換，以 \(R_{ij}\) 表示。
2. 第 \(i\) 列乘一非零常數 \(r\)，以 \(rR_i\) 表示。
3. 第 \(i\) 列乘一非零常數 \(r\) 加到第 \(j\) 列去，以 \(rR_i+R_j\) 表示。

本文中，將矩陣列運算與基本矩陣作一連結，並藉此探討利用增廣矩陣以及列運算來求乘法反矩陣的方法。

首先，我們考慮二階方陣以及 \(2\times k\)階矩陣。

設二階方陣 \(A = \left[ {\begin{array}{*{20}{c}} a&b\\ c&d \end{array}} \right]\)、以及 \(2\times k\) 階矩陣 \(B = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1k}}}\\ {{a_{21}}}&{{a_{22}}}& \ldots &{{a_{2k}}} \end{array}} \right]\)