集合的元素個數：無窮集合（三） The cardinality of a set: Infinite sets III
臺北市立和平高中教師黃俊瑋
前文〈集合的元素個數：無窮集合（二）〉提到，實數的無窮為不可數無窮。那麼，在我們常見的數系或幾何例子裡，是否容易找到比實數更大的無窮呢？以幾何的觀點來看，實數對應於一維世界的直線，讀者可能會猜測，我們僅需將維度推廣，利用二維平面的實數數對，甚至三維空間的實數數對，想必可輕易造出更大的無窮。然而，事實並非如此！
首先，我們來討論下述問題：
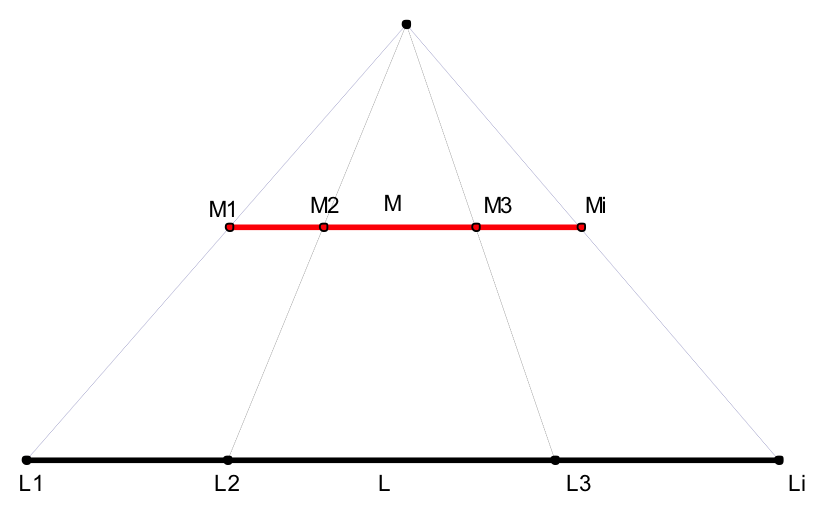
問題一：已知兩條不等長的線段 \(L\) 與 \(M\)，長度分別為 \(l\) 與 \(m\)，且 \(l>m\)，那麼，哪一條線段上的點較多呢？
直覺上，必定會認為是長度較長者點的數量較多。然而，如圖一所示，為兩不等長線段，從圖形可看出這兩條線段上的點，存在一一對應的關係。此對應圖對任意兩線段皆適用。
圖一 兩條不等長線段上的點之間，存在一一對應關係
集合的元素個數：無窮集合（二） The cardinality of a set: Infinite sets II
臺北市立和平高中教師黃俊瑋
前文〈集合的元素個數：無窮集合（一）〉之中，我們討論了自然數、整數與有理數的個數，這些集合皆為可數集。而可數無限為基數最小的無限，我們一般將此基數命作 \({\aleph _0}\)（aleph與下標零，此符號可讀作阿列夫零）。
數學家康托爾提出了，構造出基數更大集合的方法：以一集合所有子集合為元素的新集合，其基數比原集合大。譬如說吧！令 \(S = \{ 1,2,3\}\)，則所構造出的新集合為：\(\{ \{ 1,2,3\} ,\{ 1,2,3\} ,\{ 1,2\} ,\{ 1,3\} ,\{ 2,3\} ,\{ 1\} ,\{ 2\} ,\{ 3\} ,\emptyset\}\)，它共包含了 \(8\) 個元素，而 \(8\)恰為 \(2^3\)。不難看出，原集合的元素個數為 \(n\)，則新集合的元素個數為 \(2^n\)。因此，我們可構造出一個基數為 \(2^{\aleph _0}\) 的新集合，如此可不斷地構造出更大的集合。
而我們把 \({\aleph _0}\)、\(2^{\aleph _0}\) 等涉及無窮集合的基數稱為超限基數（transfinite cardinal number）。
那實數呢？問題似乎變難了，不像整數或有理數易於排序，我們很難有系統地將實數重新排序，使其與自然數一一對應，換言之，實數的個數問題，顯得更難以掌握。所以，我們不禁懷疑，實數的個數與自然數一樣多嗎？
集合的元素個數：無窮集合（一） The cardinality of a set: Infinite sets I
臺北市立和平高中教師黃俊瑋
無窮集合元素個數相等的定義如下：
若兩個集合（無窮集合）之間存在一一對應關係，則這兩個集合的元素個數相等。
我們可藉此發現許多違反直覺的例子。首先，就直觀上來看，正整數的個數比正偶數的個數來得多，而正整數的個數也比完全平方數來得多，不過，我們依上述定義實際作對應與比較後，會發現：
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\2&4&6&8&10&\cdots&2n\end{array}\)
換言之，正整數的個數與正偶數的個數一樣多。類似地，我們也會發現：
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\1^2&2^2&3^2&4^2&5^2&\cdots&n^2\end{array}\)
因此，正整數的個數與平方數的個數一樣多。這是不是既違反直覺又不可思議呢？