多項式
多項式 (Polynomial)
國立中央大學數學系單維彰副教授責任編輯
選定一個具備實數運算性質的符號,稱為元,元與其本身和其他實數做有限多次加、乘計算所成的式子,稱為多項式。我們通常以$${x}$$作為元,但也可以用其他符號。例如 $${x}$$、$${x+1}$$、$${x^2}$$、$${2{x}^2-{x}+1}$$ 都是多項式,又特別稱為 $${x}$$ 的多項式。
注意 $${-x}$$ 是 $${(-1)}\times {x}$$ 的意思,而 $$\frac{1}{x}$$、$$\sqrt{x}$$ 都不是多項式。
自乘 $${n}$$ 次的 $${x}$$ 記作 $${x^n}$$,這一項次數是 $${n}$$;在這一整篇中,都令 $${n}$$ 是 $$0$$ 或正整數;注意 $${x^0=1}$$。令 $${a}$$ 是任意實數,稱 $${ax^n}$$ 是 $${x}$$ 的 $$n$$ 次項,而 $${a}$$ 是此項的係數。例如在多項式 $${9{x}^2+{x}+3}$$ 中,二次項的係數是 $$9$$,一次項的係數是 $$1$$,零次項的係數是 $$3$$;零次項的係數又稱為常數項。
書寫多項式時,我們習慣按照次數由高到低依序而寫,如 $${x^5-4x+1}$$,這樣的書寫方式我們稱之為降冪形式。而若反過來,按次數由低到高排列,如 $${1-4x+x^5}$$,則稱之為升冪形式。
多項式中最高次那一項的次數,稱為多項式次數。$${n}$$ 次多項式的一般形式為
$${{a}_{n}{x}^{n}}+{{a}_{n-1}x^{n-1}}+$$…..$${+{{a}_{1}{x}}+{a_0}}$$,$${a_n},…..,{a_1}$$, $${a_0}\in \mathbb{R}$$,其中$${{a_n} \neq 0}$$。
若以 $${P}$$ 簡記此多項式,則寫成 $${P}={{a}_{n}{x}^{n}}+{{a}_{n-1}x^{n-1}}+…..{+{{a}_{1}{x}}+{a_0}}$$。多項式 $${P}$$ 的次數為則記作 $$\mathrm{deg}~{P}$$。
按照多項式的定義,一個實數也是一個多項式,稱為常數多項式。如果 $${a \neq 0}$$,則 $${a}$$ 是一個零次多項式。而 $$0$$ 特別稱為零多項式;我們不討論零多項式的次數。所以多項式包含了實數。
雖然我們賦予多項式中的「元」與實數相同的加、乘規則,但是它不對應數線上的任何一點,所以多項式不在數線上(除了常數多項式以外),多項式之間不能比較大小,只有相等或者不相等的關係。當兩個多項式具有相同次數的項,而且同次項的係數都相等,則稱兩個多項式相等,並且用等號記之。例如 $${x^4-x^3+2x^3}$$ 與 $${x^4+x^3}$$ 相等,記作 $${x^4-x^3+2x^3} = {x^4+x^3}$$ ;這是因為,基於實數乘法對加法的分
配律:$${x^4-x^3+2x^3} = {x^3}{(x-1+2)} = {x^3}{(x+1)} = {x^4}+{x^3}$$。但是,$${x^2} \neq {x}$$。
基本上,應用分配律就能做多項式相加、相減和相乘的運算。而若 $${P}$$、$${Q}$$ 為多項式,則 $${P}-{Q} = {P}+{((-1) \times {Q})}$$,所以我們不必討論多項式的減法計算。執行多項式的加法時,只要對次數相同的項做係數加法即可,稱為同類項合併。例如 $${x^4}-{5x^2}+3x-7$$ 與 $${4x^3-3x^2-2x+3}$$ 相加,其記號和過程如下:
$$({x^4}-{5x^2}+3x-7)+{(4x^3-3x^2-2x+3)}$$
$$={x^4+4x^3-5x^2-3x^2+3x-2x-7+3}$$ (加法交換律)
$$={x^4+4x^3-{x^2}{(5+3)}+x(3-2)+(3-7)}$$ (分配律)
$$={x^4+4x^3-8x^2+x-4}$$
然而,觀察多項式和十進制數字有緊密關連。例如
$$1923 = 1 \times 1000 + 9 \times 100 +2 \times 10 +3 \times 1$$
是十進制數字的意義,若我們將上式中的 $$10$$ 以 $${x}$$ 代替,則可以寫成三次多項式 $${x^3+9x^2+2x+3}$$。所以,兩個整數的加(減)法直式計算,可以推廣成多項式的加(減)法直式計算。例如 $${x^4-5x^2+3x-7}$$ 與 $${4x^3-3x^2-2x+3}$$ 相加,可以列直式如下,對齊各次項:
而整數的加(減)法直式計算相當於省略 $${x}$$ 不寫,只依序寫出各次項的係數(千位數、百位數、十位數、個位數)。類似地,我們也可以在多項式直式加法中,只依序寫出各次項的係數,稱之為分離係數法。採用分離係數法時必須注意,若多項式中有缺項,須用 $$0$$ 佔位,如下方紅色標示。
多項式之間的乘法可根據指數律操作。例如 $${4x^3-3x^2-2x+3}$$ 與 $${x^2-3}$$ 相乘,其記號和程序如下:
$${4x^3-3x^2-2x+3} \times {(x^2 – 3)}$$
$$={x^{2} \times (4x^3-3x^2-2x+3) -3 \times (4x^3-3x^2-2x+3)}$$ (交換律和分配律)
$$={4x^5-3x^4-2x^3+3x^2-12x^3+9x^2+6x-9}$$ (指數律)
$$={4x^5-3x^4- {x^3}(2+12) + {x^2}(3+9)+6x-9}$$ (同類項合併)
$$={4x^5-3x^4-14x^3+11x^2+6x-9}$$
而多項式的直式乘法如下。
而根據實數的運算性質,所有乘以零的數皆為零,同樣地 $${x}\times 0 = 0$$,因此綠色那一列的運算其實可以省略:
分離係數法亦可在多項式的乘法中實作,但一樣要注意之前所提的補 $$0$$ 原則:
多項式的除法類似正整數的除法,我們以另一篇文件整理。
多項式可以寫成等式,稱為方程式,則「元」的意義就成了「未知數」,例如 $${x^2-3x+2 =0}$$ 有兩個解。多項式可以寫成函數,則「元」的意義就成了「變數」,例如函數 $${f(x)} = {x^2-3x+2}$$ 的圖形開口向上。但是,$${P} ={ x^2-3x+2}$$ 並非方程式,它的意思是「令 $${P}$$ 代表多項式 $${x^2-3x+2}$$」;而 $${x^2-3x+2 = (x-2)(x-1)}$$ 也不是方程式,它的意思是等號兩側的多項式相等。在前面兩個例子裡 $${x}$$ 既不是未知數也不是變數,它就是一個「元」。


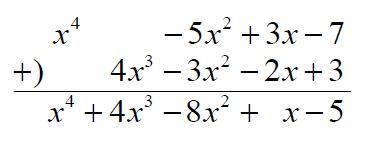

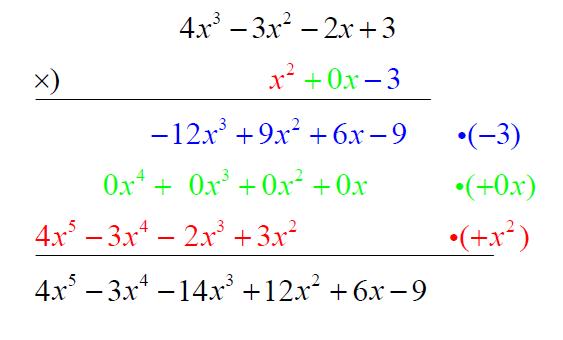
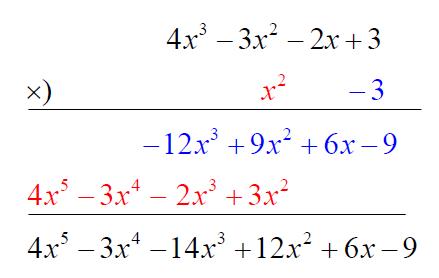
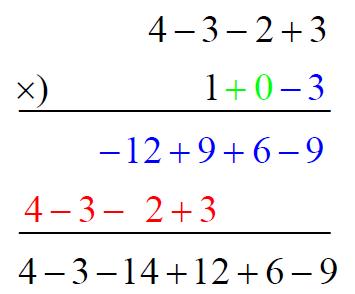
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題 

為何零多項式不是零次多項式的一種?