平方數和與立方數和

平方數和與立方數和 (Sums of Squares and Sums of Cubes)
國立屏東高級中學數學科楊瓊茹老師/國立臺灣師範大學數學系洪萬生教授責任編輯

在高中數學的「數列與級數」單元中，有三個眾所周知的級數和公式：

$$\displaystyle 1+2+3+\mbox{…}+n=\frac{n(n+1)}{2}$$

$$\displaystyle 1^2+2^2+3^2+\mbox{…}+n^2=\frac{1}{6}n(n+1)(2n+1)$$

$$\displaystyle 1^3+2^3+3^3+\mbox{…}+n^3=[\frac{1}{2}n(n+1)]^2$$

並且都必須用「數學歸納法」加以證明。於是，教師費盡唇舌的解釋「數學歸納法」以及賣力的證明，但是，對於尚未充分理解「數學歸納法」的學生而言，只能依樣畫葫蘆地按步驟表面操弄，並且記住公式，如此單一的學習方式似乎顯得徒勞無功。換句話說，教師使用「數學歸納法」在邏輯上嚴格證明等式恆成立，但是，證明本身能否激發學生多少數學思維？甚至在證明之前，學生對於題目本身的瞭解和體會究竟有多少？

例如：
$$1^2+2^2+3^2+\mbox{…}+n^2=$$？
$$1^3+2^3+3^3+\mbox{…}+n^3=$$？

這兩個級數和究竟如何得知的呢？

筆者認為相較於形式嚴謹的證明，如果讓初學者先從一個美妙的圖形實例開始思索，體驗到數學發現的過程，例如：觀察、猜想、歸納、試驗、確認和總結出之所以如此的理由，那麼，這一類問題的意義便可瞭然於胸。因此，筆者要補充另外的證明方式以供參考。

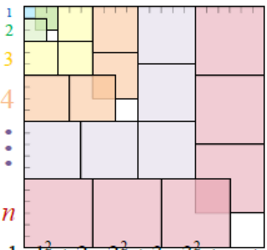
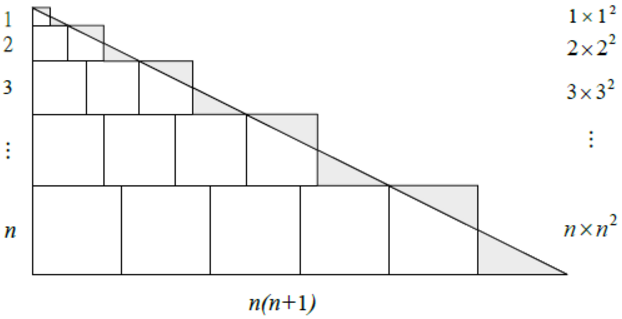
在美國數學協會（The Mathematical Association of America，簡稱MAA）出版的Proofs Without Words 中，編入許多不用文字的證明，底下(1)、(2)，是摘錄平方數和的圖形；立方數和的圖形參見 (3)、(4)、(5)、(6)；至於自然數的和在此不贅述。

（1）$$1^2+2^2+3^2+\mbox{…}+n^2=\frac{1}{3}n(n+1)(n+\frac{1}{2})$$

（2）$$3(1^2+2^2+3^2+\mbox{…}+n^2)=\frac{1}{2}n(n+1)(2n+1)$$

（3）$$1^3+2^3+3^3+\mbox{…}+n^3=(1+2+3+\mbox{…}+n)^2$$

（4）$$1\times{1}^2+2\times{2}^2+3\times{3}^2+\mbox{…}+n\times{n}^2=\frac{1}{4}(n^2+n)^2$$

（5）$$1\times{1}^2+2\times{2}^2+3\times{3}^2+\mbox{…}+n\times{n}^2=(1+2+3+\mbox{…}+n)^2$$

（6）$$1\times{1}^2+2\times{2}^2+3\times{3}^2+\mbox{…}+n\times{n}^2=\frac{1}{2}(n)(n+1)(1+2+3+\mbox{…}+n)$$

$$1+2+3+\cdots+n=\frac{1}{2}n(n+1)$$

這些是數學裡可以「看到」的幾何實例，一看就懂、不證自明，而不是抽像的符號或是不易領會的理論。倘若在課堂上偶爾建構一個既簡潔又巧妙的圖形，對學生而言或許是驚喜和深刻的印象。誠然，圖形在教學上扮演有意義的角色，但是數學家對它的「正當性」有所保留，誠如柏拉圖在他的《理想國》中強調吾人在心靈思考數學客體時，千萬不可被圖形所迷惑或左右。畢竟，數學上有需多細節和陷阱，致使數學家必須秉持邏輯論證，要求文字形式上嚴密的證明。所以，採用「數學歸納法」證明級數和公式亦有其考量。因此，圖形的直觀與形式證明的嚴謹各有其優點，將兩者適時鋪陳以呈現最佳教學策略。

參考資料
Roger B. Nelsen (1993). Proofs without Words: Exercises in Visual Thinking. Washington, DC: MAA。
洪萬生 (2007). 〈圖說一體、不證自明〉，《HPM 十年風華》，高中數學學科中心。