多項式函數圖形的遞增、遞減與凹凸性（Increasing, Decreasing, Concave and ConvexProperties of Polynomial Functions）

多項式函數圖形的遞增、遞減與凹凸性（Increasing, Decreasing, Concave and ConvexProperties of Polynomial Functions）
國立台南第一高級中學數學科林倉億老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要:本文說明多項式函數圖形的遞增、遞減、凹向上、凹向下，以及在區間 上的遞增函數、嚴格遞增函數、遞減函數、嚴格遞減函數、單調函數。

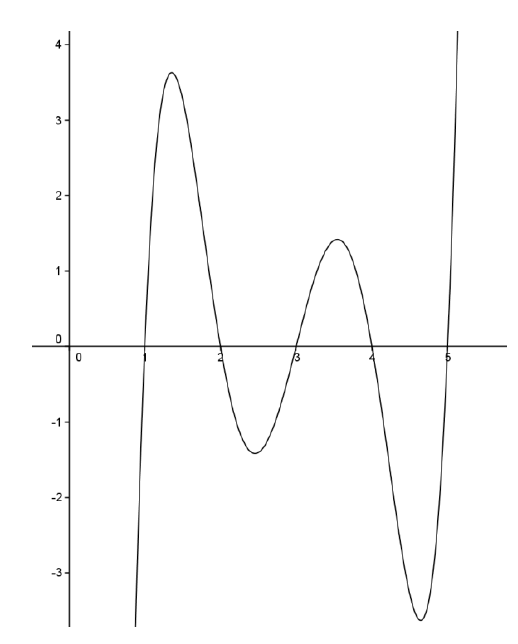
藉助今日科技發展之便，只要打開電腦，執行數學繪圖軟體程式，然後任意輸入一個多項式函數，一瞬間，它的圖形就會顯示在眼前。例如下圖就是利用數學繪圖軟體GeoGebra所繪的 $$f(x)=(x-1)(x-2)(x-3)(x-4)(x-5)$$ 之圖形。

然而，在沒有電腦的時代，人們是如何繪製、研究多項式函數的圖形呢？觀察多項式函數的圖形，可以發現構成圖形的基本組成不外是下列幾種：

圖一至圖三代表的是直線，是一次函數或常數函數才會有的圖形，故一次函數與常數函數又合稱為「線型函數」。至於剩下的四種曲線，則是二次以上的函數圖形才會出現的。現在我們該怎麼將這七種圖形分類呢？

首先，若將圖形視為坐標平面上的路徑，則沿著路徑向右走（ $$x$$ 坐標增加），在圖一、圖四與圖五中，位置會不斷地向上移動（ $$y$$ 坐標增加）；在圖三、圖六與圖七中，位置會不斷地向下移動（ $$y$$ 坐標減少）；而在圖二之中，位置則一直保持水平（ $$y$$ 坐標不變）。這種 $$y$$ 坐標隨著 $$x$$ 坐標增加而變化的性質，我們就稱為函數的遞增、遞減，用數學符號定義如下：

$$f(x)$$ 為多項式函數，$$x_1$$ 與 $$x_2$$ 是區間 $$[a,b]$$ （註一）內的任意兩數，且 $$x_1<x_2$$：

1. 若 $$f(x_1)\le f(x_2)$$ 恆成立，則稱 $$f(x)$$ 在區間 $$[a,b]$$ 上為「遞增函數」。
2. 若 $$f(x_1)< f(x_2)$$ 恆成立，則稱 $$f(x)$$ 在區間 $$[a,b]$$ 上為「嚴格遞增函數」。
3. 若 $$f(x_1)\ge f(x_2)$$ 恆成立，則稱 $$f(x)$$ 在區間 $$[a,b]$$ 上為「遞減函數」。
4. 若 $$f(x_1)> f(x_2)$$ 恆成立，則稱 $$f(x)$$ 在區間 $$[a,b]$$ 上為「嚴格遞增函數」。

無論 $$f(x)$$ 在區間 $$[a,b]$$ 上為「遞增函數」或「遞減函數」，統稱 $$f(x)$$ 在區間 $$[a,b]$$ 上為「單調函數」。

因此，若圖一至圖七是代表不同的多項式函數在區間 $$[a,b]$$ 上的圖形，則圖一、圖四與圖五表示對應的函數在區間 $$[a,b]$$上為「嚴格遞增函數」，當然也可稱為「遞增函數」。圖三、圖六與圖七表示對應的函數在區間 $$[a,b]$$ 上為「嚴格遞減函數」，當然也可稱為「遞減函數」。
那圖二呢？顯然它是常數函數 $$f (x) = k$$（$$k$$ 為常數）的圖形，照上面的定義方式，說它在區間 $$[a,b]$$ 上為「遞增函數」或「遞減函數」，其實都可以。

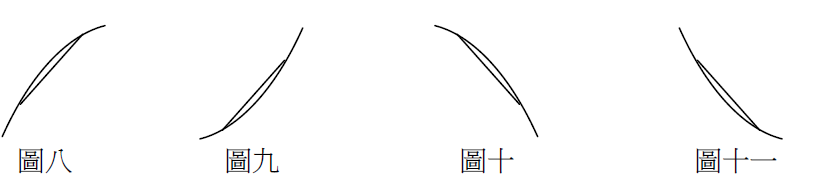
圖四與圖五這兩種曲線都代表函數在區間 $$[a,b]$$ 上是（嚴格）遞增函數，但兩者看起來並不像。不一樣的地方是，在圖四上任兩點所連成的線段必在圖形的下方（如圖八），我們稱具此性質的圖形為「凹口向下」，簡稱「凹向下」；而在圖五上任兩點所連成的線段必在圖形的上方（如圖九），我們稱之為「凹口向上」，簡稱「凹向上」。同樣地，圖六是「凹向下」，而圖七是「凹向上」（如圖十、十一）。

綜合說來，除了線型函數外，多項式函數圖形的特性，我們可以再從「遞增」、「遞減」、「凹向上」與「凹向下」來做更進一步的細分。事實上，在往後的微積分課程之中，我們將會學到利用一階導數與二階導數來判別這些特性，並作更完整、詳盡的說明。

註一：區間 $$[a,b]=\{x|~a\le x\le b\}$$，即介於 $$a$$、$$b$$ 之間（包含 $$a$$、$$b$$）的所有實數。

參考資料：

1. 林福來等 (2011)，《普通高級中學數學第一冊》，南一書局。