初等的機率論（8）隨機變數及其種種性質（Random Variables and Its properties）

初等的機率論（8）隨機變數及其種種性質
（Elementary Probability Theory-8. Random Variables and Its properties）
國立臺灣大學數學系蔡聰明副教授/國立臺灣大學數學系蔡聰明副教授責任編輯

連結：初等的機率論（7）獨立事件的概念

摘要：本文分別介紹「離散型」與「連續型」機率分佈（probability distribution）中幾個重要的分佈：「二項分佈（binomial distribution）」、「Poisson分佈」、「常態分佈（normal distribution）」，進而導出其期望值與變異數。並將「Markov不等式」與「Chebyshev不等式」以機率的語言重述之。

一個隨機實驗做下來，就有初等機率空間 $$(\Omega,\mathfrak{A},P)$$，這是精煉隨機實驗所得到的原始機率資料。然而，我們有興趣觀測的往往是某個變量 $$X$$，定義在 $$\Omega$$ 上的一個實值函數 $$X:\Omega\rightarrow\mathbb{R}$$。這就是隨機變數的概念，在統計學上又叫做統計變量。$$X$$ 將 $$(\Omega,\mathfrak{A},P)$$ 上的機率資料，重新改訂成方便於使用的資訊。例如丟兩個骰子，我們要觀測「點數和」是多少。在每一賭局中，賭徒要觀察輸贏額。

透過隨機變數才能挖掘出深刻而有意義的事件。例如大數法則與中央極限定理裡所涉及的美妙事件。

甲、隨機變數

【定義 5】任何一個定義在樣本空間 $$\Omega$$ 上的實值函數 $$X:\Omega\to\mathbb{R}$$，就叫做一個隨機變數（random variable）。對於任意實數的子集 $$E\subset \mathbb{R}$$，事件 $$\{X\in E\}$$ 定義為 $$\{\omega\in\Omega:X(\omega)\in E\}$$。我們也將機率 $$P(\{X\in E\})$$ 簡寫為 $$P(X\in E)$$。

【註】一個有趣的觀察是，根據這個定義，隨機變數「既不隨機也不是變數」，有點兒禪味。因為它是一個函數，並且也不涉及機率。之所以採用隨機變數之名有其歷史的約定俗成理由。

【例14】考慮丟兩個銅板的隨機實驗，樣本空間為 $$\Omega=\{HH,HT,TH,TT\}$$。

令 $$X:\Omega\rightarrow\mathbb{R}$$ 定義為 $$X(HH)=2,~~X(HT)=X(TH)=1,~~X(TT)=0$$

則 $$X$$ 表示出現正面次數的隨機變數。

乙、機率分佈

因為我們的 $$\Omega=\{\omega_1,\omega_2,\dots,\omega_N\}$$ 是有限集，

所以隨機變數 $$X$$ 也只取有限數值 $$\{x_1,x_2,\dots,x_m\}$$

使得 $$f(x_k)\equiv P\{X=x_k\}$$ 皆為正數並且 $$\sum\limits_{k=1}^m f(x_k)=1$$

這種 $$X$$ 叫做「離散型且取有限個值」的隨機變數。

定義如上的離散函數 $$f:\{x_1,x_2,\dots,x_m\}\rightarrow[0,1]$$

我們稱之為隨機變數 $$X$$ 的機率分佈（probability distribution）或者機率密度函數（probability density function）。

$$(1)$$ 離散型且有限個取值的機率分佈

若離散函數 $$f$$，在有限個點取值，滿足下列兩個條件，那麼 $$f$$ 就是某個隨機變數 $$X$$的機率分佈：

$$(\mathrm{i})~~~0\le f(x_k)\le 1,~k=1,2,\cdots,m$$
$$(\mathrm{ii})~\sum\limits^m_{k=1}f(x_k)=1$$

【習題】試造一個機率空間與隨機變數使得具有上述的機率分佈。

【例15】（二項分佈）

考慮丟一個銅板，

出現正面 $$H$$ 的機率為 $$p,~~0<p<1$$，出現反面 $$T$$ 的機率為 $$q(=1-p)$$。

（當 $$p=1/2$$ 時，就是一個公正銅板（a fair coin））。

因為我們要點算出現正面的次數，所以定義隨機變數 $$\xi$$ 為：

當出現正面 $$H$$，$$\xi(H)=1$$，機率為 $$p$$
當出現反面 $$T$$，$$\xi(T)=0$$，機率為 $$q$$

今將此銅板在相同條件下獨立地丟 $$n$$ 次，我們要來觀測出現正面的次數。

首先是建立機率模型。這就是三合一的古典機率空間 $$(\Omega_n,\mathfrak{A}_n,P_n)$$：

樣本空間 $$\Omega_n=\{\omega=(\omega_1,\omega_2,\cdots,\omega_n):\omega_k=H~or~T,~k=1,2,\cdots,n\}$$

事件的全體 $$\mathcal{A}_n=2^{\Omega_n}$$，$$\Omega_n$$ 的羃集（power set）

對於樣本點 $$\omega_n\in\Omega$$ 如何指定機率？

如果在 $$\{\omega_1,\omega_2,\dots,\omega_n\}$$ 中含有 $$r$$ 個 $$H$$ 且 $${n}-r$$ 個 $$T$$，

那麼就定義 $$P_n(\{\omega\})=p^rq^{n-r}$$，並且 $$P_n(A)=\sum\limits_{\omega\in A}P_n(\omega)$$

再考慮隨機變數 $$\xi_{k}:\Omega_n\rightarrow\{0,1\}$$

$$\xi_k(\omega)=\left\{\begin{array}{ll}1,&\mathrm{if}~\omega_k=H\\0,&\mathrm{if}~\omega_k=T\end{array}\right.~~~~~~k=1,2,\cdots,n$$

這是觀測第 $$k$$ 次丟銅板的狀況。我們就得到一列獨立且具有相同分佈 $$\mathrm{(i.i.d)}$$ 的隨機變數 $$(\xi_k)_{k=1,2,\cdots,n}$$，叫做銅板序列（a coin tossing sequence）。

最後定義隨機變數 $$S_{n}:\Omega_n\rightarrow\{0,1,2,…,n\}$$ 為

$$S_n=\xi_1+\xi_2+\cdots+\xi_n$$

那麼 $$S_n$$的機率分佈為

$$P(S_n=k)=C^n_kp^kq^{n-k},~~~k=0,1,2,\cdots,n$$

這叫做二項分佈，因為它涉及二項定理：

$$1=(p+q)^n=\displaystyle\sum^n_{k=1}C^n_kp^kq^{n-k}$$

【定義 6】（二項分佈）

如果一個隨機變數 $$X:\Omega\to\{0,1,2,3,\cdots,n\}$$ 具有如下的離散型之機率分佈：

$$f:\{0,1,2,\cdots,n\}\to[0,1]$$

$$f(k)=C^n_kp^kq^{n-k},~~~k=0,1,2,\cdots,n$$

則稱 $$X$$ 為具有二項分佈（binomial distribution），記為 $$X\sim B(n,p)$$。

二項分佈是整個古典機率論的出發點（參見後述），由此出發可以一路探索機率法則（laws of chance），例如大數法則與中央極限定理，成果非常豐碩。

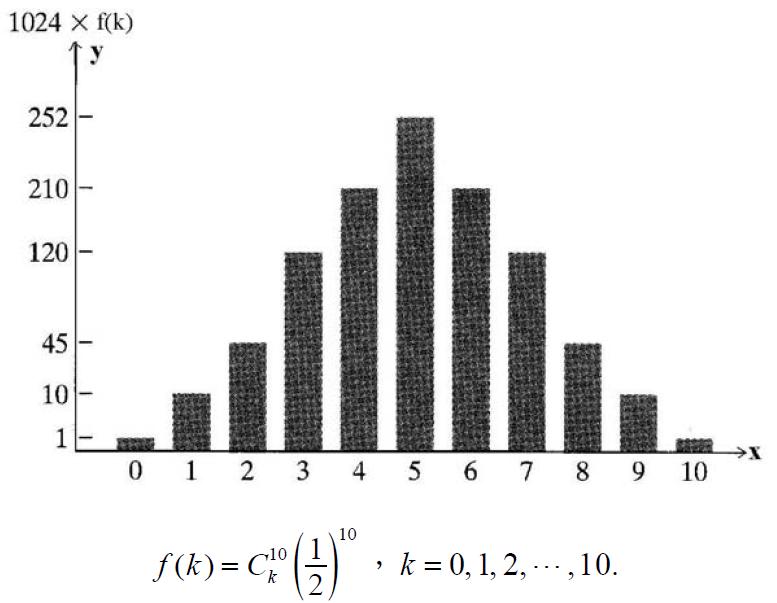
【例16】若 $$X\sim B(10,1/2)$$，即獨立丟一個公正銅板 $$10$$ 次，$$X$$ 表示出現正面次數的隨機變數。在下圖中，我們作出 $$X$$ 的機率分佈函數圖，為方便起見，我們將 $$y$$ 軸放大 $$1024$$ 倍。

$$(2)$$ 離散型且無限個取值的機率分佈

若離散函數 $$f$$，取值於可列個（countable）無限點，滿足下列兩個條件，那麼 $$f$$ 就是某個隨機變數 $$X$$ 的機率分佈：

$$(\mathrm{i})~~~0\le f(x_k)\le 1,~k=1,2,\cdots,n,\cdots$$
$$(\mathrm{ii})~\sum\limits^\infty_{k=1}f(x_k)=1$$

若 $$f(x_k)>0$$，則 $$x_k$$ 稱為 $$X$$ 的可能值（a possible value）。

【註】若 $$X$$ 的可能值為可列無窮，則不能每個值的機會均等。

【習題】試造一個機率空間與隨機變數使得具有上述的機率分佈。

【定義 7】（Poisson 分佈）

如果一個隨機變數 $$X:\Omega\to\{0,1,2,3,\cdots,k,\cdots\}$$ 具有如下的機率分佈：

$$\displaystyle f(k)=\frac{e^{-\lambda}\lambda^k}{k!\ },~~~k=0,1,2,3,\cdots,n,\cdots$$，其中 $$\lambda>0$$

則稱 $$X$$ 具有 Poisson 分佈，以 $$\lambda$$ 為參數，記成 $$X\sim P(\lambda)$$

這裡我們要用到一點兒微積分的極限與級數概念：

$$\displaystyle e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n\approx 2.718281828$$

以及 $$\displaystyle e^\lambda=1+\lambda+\frac{\lambda^2}{2!\ }+\frac{\lambda^3}{3!\ }+\cdots+\frac{\lambda^k}{k!\ }+\cdots$$

從而 $$\displaystyle\sum^\infty_{k=0}\frac{e^{-\lambda}\lambda^k}{k!\ }=1$$

對於離散型的機率分佈，我們可以這樣想像：數量為 $$1$$ 的一桶機率水，如下雨般分佈到 $$X$$ 的值域的每一點上面。

二項分佈與Poisson分佈是離散型分佈中最重要的兩個機率分佈。

$$(3)$$ （絕對）連續型機率分佈

在更高等的機率論中，我們會遇到隨機變數 $$X$$ 連續取值於實數系的情形。它的機率分布就是（絕對）連續型的機率分布（（absolutely）continuous probability distribution）。

此時一定要用到微積分。在微積分中有離散的差和分與連續的微積分之平行類推：

差分$$\Delta$$，不定和分$$\sum$$，定合分$$\sum\limits^n_m\longleftrightarrow$$ 微分$$d$$，不定積分$$\int$$，定積分$$\int^b_a$$

下面我們就來施展這個類推。

如果 $$f$$ 是一個可積分函數，取值於實數系 $$\mathbb{R}$$，滿足下列兩個條件，那麼 $$f$$ 就是某個隨機變數 $$X$$ 的機率分佈：

$$(\mathrm{i})~~~f(x)\ge 0,~~\forall x\in\mathbb{R}$$
$$(\mathrm{ii})~\displaystyle\int^\infty_{-\infty}f(x)~dx=1$$

並且隨機變數 $$X$$ 取值於 $$A\subset\mathbb{R}$$的機率為 $$P(A)=\int_{A}f(x)dx$$。我們稱 $$X$$ 為一個（絕對）連續型隨機變數，而 $$f(x)$$ 叫做 $$X$$ 的機率分佈或機率密度函數。

在機率論與統計學中，最重要的（絕對）連續型分佈就是正規分佈（normal distribution），又叫做常態分佈。

【定義 8】（正規分佈或常態分佈）

設 $$\mu\in\mathbb{R}$$，$$\sigma>0$$。如果一個隨機變數 $$X$$ 取值於 $$\mathbb{R}$$，具有如下的機率分佈：

$$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2},~~~\forall x\in\mathbb{R}~~~~~~~~~(1)$$

則稱 $$X$$ 具有正規分佈或常態分佈，以 $$\mu$$ 與 $$\sigma^2$$ 為參數，記成 $$X\sim N(\mu,\sigma^2)$$

當 $$\mu=0,~\sigma=1$$ 時，機率分佈函數為：

$$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2},~~~\forall x\in\mathbb{R}~~~~~~~~~(2)$$

叫做標準正規分佈（或標準常態分佈）（standard normal distribution），記成 $$X\sim N(0,1)$$

【注意】$$(1)$$ 與 $$(2)$$ 式的 $$f(x)$$ 都具有：$$(\mathrm{i})~f(x)\ge 0,\forall x\in\mathbb{R}$$，$$(\mathrm{ii})~\int\limits^{\infty}_{-\infty}f(x)dx=1$$ 的性質，這恰是 $$f(x)$$ 成為機率密度函數的條件。

丙、期望值與變異數

【定義 9】（數學期望值，簡稱期望值，又叫做平均值）

$$(\mathrm{i})$$ 如果 $$X$$ 為離散型隨機變數，取值 $$x_1,x_2,x_3,\cdots$$，並且具有機率密度函數 $$f(x_k)$$，則 $$X$$ 的期望值（expectation）定義為

$$E(X)=\displaystyle\sum_k x_kf(x_k)$$ （Lebesgue式的和分）

 $$(\mathrm{ii})$$ 如果 $$X$$ 為連續型隨機變數，取值 $$\mathbb{R}$$，並且具有機率密度函數 $$f(x)$$，則 $$X$$ 的期望值定義為

$$E(X)=\displaystyle\int_{-\infty}^{\infty}xf(x)dx$$

但必須這個積分存在。

我們經常用$$\mu$$ 來代表期望值，即 $$\mu\equiv{E(X)}$$，這方便於我們定義變異數與標準偏差。

【定義 10】（變異數與標準偏差）

隨機變數 $$X$$ 的變異數 $$var(X)$$ 定義為 $$var(X)=E[(X-\mu)^2]\equiv \sigma^2$$

對於離散型隨機變數

$$var(X)=E[(X-\mu)^2]=\sum\limits_k(x_k-\mu)^2f(x_k)$$

對於連續型隨機變數

$$var(X)=E[(X-\mu)^2]=\int\limits^{\infty}_{-\infty}(x-\mu)^2f(x)dx$$

【註】變異數的計算經常按下面的公式：

$$\begin{array}{ll}var(X)&=E[X-E(X)]^2=E[X^2-2XE(X)+(E(X))^2]\\&=E(X^2)-2E(X)E(X)+[E(X)]^2=E(X^2)-[E(X)]^2\end{array}$$

【例17】若隨機變數$$X\sim B(n,p)$$，即二項分佈，則 $$E(X)=np$$，$$var(X)=npq$$

【解答】期望值

$$\begin{array}{ll}E(X)&=\displaystyle\sum^n_{k=0}kC^n_kp^kq^{n-k}=\sum^n_{k=0}k\frac{n!\ }{k!\ (n-k)!\ }p^kq^{n-k}\\&\displaystyle=np\sum^n_{k=0}k\frac{(n-1)!\ }{(k-1)!\ [(n-1)-(k-1)]!\ }p^{k-1}q^{(n-1)-(k-1)},~~~i=k-1\\&\displaystyle=np\sum^n_{i=0}k\frac{(n-1)!\ }{i!\ [(n-1)-i]!\ }p^iq^{(n-1)-i}=np\end{array}$$

同理可算得 $$E(X^2)=np[(n-1)p+1]$$。

從而變異數為 $$var(X)=E(X^2)-[E(X)]^{2}=np[(n-1)p+1]-(np)^2=npq$$

【例18】若隨機變數 $$X$$～$$P(\lambda)$$，則 $$E(X)=\lambda$$，$$var(X)=\lambda$$。

Poisson分佈的期望值與變異數相同，皆為 $$\lambda$$，這是奇妙的。

【解答】

先算期望值

$$\begin{array}{ll}E(X)&=\displaystyle \sum^{\infty}_{k=0}k\frac{e^{-\lambda}\lambda^k}{k!\ }=\lambda\sum^{\infty}_{k=1}\frac{e^{-\lambda}\lambda^{k-1}}{(k-1)!\ }\\&\displaystyle=\lambda e^{-\lambda}\sum^{\infty}_{k=1}\frac{\lambda^{k-1}}{(k-1)!\ }=\lambda e^{-\lambda}\sum^{\infty}_{k=0}\frac{\lambda^k}{k!\ }\\&=\lambda e^{-\lambda}e^{\lambda}=\lambda\end{array}$$

再計算 $$E(X^2)$$：

$$\begin{array}{ll}E(X^2)&=\displaystyle\sum^{\infty}_{k=0}k^2\frac{e^{-\lambda}\lambda^k}{k!\ }=\lambda\sum^{\infty}_{k=1}\frac{ke^{-\lambda}\lambda^{k-1}}{(k-1)!\ }\\&=\displaystyle \lambda\sum^{\infty}_{k=0}\frac{(k+1)e^{-\lambda}\lambda^k}{k!\ }=\lambda\left[\sum^{\infty}_{k=0}\frac{ke^{-\lambda}\lambda^k}{k!\ }+\sum^{\infty}_{k=0}\frac{e^{-\lambda}\lambda^k}{k!\ }\right]\\&=\lambda(\lambda+1)\end{array}$$

於是變異數為 $$var(X)=E(X^2)-E(X)^2=\lambda(\lambda+1)-\lambda^2=\lambda$$

【例19】若隨機變數$$X\sim N(\mu,\sigma^{2})$$，則$$E(X)=\mu$$，$$var(X)=\sigma^2$$

【解答】

期望值 $$E(X)=\frac{1}{\sqrt{2\pi}\sigma}\int\limits^{\infty}_{-\infty}xe^{-(x-\mu)^2/2\sigma^2}dx$$。用 $$(x-\mu)+\mu$$ 替換 $$x$$ 得到

$$\displaystyle E(x)=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}(x-\mu)e^{-(x-\mu)^2/2\sigma^2}dx+\mu\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}e^{-(x-\mu)^2/2\sigma^2}dx$$

令 $$y=x-\mu$$，則得

$$\displaystyle E(x)=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}ye^{-y^2/2\sigma^2}dy+\mu\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}e^{-(x-\mu)^2/2\sigma^2}dx$$

第一項的被積分函數為奇函數，故第一項為 $$0$$，於是 $$E(X)=\mu$$。

變異數為 $$\displaystyle var(X)=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}(x-\mu)^2e^{-(x-\mu)^2/2\sigma^2}dx$$

作變數代換 $$y=(x-\mu)/\sigma$$，則得 $$\displaystyle var(X)=\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}y^2e^{-y^2/2}dy$$，

利用分部積分法 $$\displaystyle=\frac{\sigma^2}{\sqrt{2\pi}}\left[-ye^{-y^2/2}\Big|^{\infty}_{-\infty}+\int^{\infty}_{\infty}e^{-y^2/2}dy\right]\\=\displaystyle \sigma^2\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}e^{-y^2/2}dy=\sigma^2$$

期望值就是和分或積分，故具有加性（additivity）：

設 $$X$$ 與 $$Y$$ 為兩個隨機變數，則有

$$E(X+Y)=E(X)+E(Y)$$

進一步，設 $$X_1,X_2,\cdots,X_n$$ 為 $$n$$ 個隨機變數，則有

$$E(X_1+X_2+\cdots+X_n)=E(X_1)+E(X_2)+\cdots+E(X_n)$$

對於變異數的計算，因為涉及平方，所以就沒有單純的加性，必須要有額外的獨立性條件，加性才會成立。

但是對於係數乘積卻有：$$var(\alpha X)=\alpha^2var(X)$$，其中 $$\alpha$$ 為一個常數。

因為

$$\begin{array}{ll}var(\alpha X)&=E[(\alpha X)^2]-[E(\alpha X)]^2\\&=\alpha^2E(X)^2-[\alpha E(X)]^2\\&=\alpha^2[E(X)^2-[E(X)]^2]\\&=\alpha^2var(X)\end{array}$$

【定義 10】（隨機變數的獨立性）

$$(\mathrm{i})$$ 假設 $$X$$ 與 $$Y$$ 為兩個隨機變數，如果對於任何兩個實數子集 $$A$$ 與 $$B$$ 都有

$$P(X\in A,~Y\in B)=P(X\in A)P(Y\in B)$$

則稱 $$X$$ 與 $$Y$$ 是獨立的（independent）。

$$(\mathrm{ii})$$ 假設 $$X_1,X_2,\cdots,X_n$$ 為 $$n$$ 個隨機變數，如果對於任何實數子集 $$A_1,A_2,\cdots,A_n$$ 下式都成立：

$$\displaystyle P(X_1\in A_1,~X_2\in A_2,\cdots,~X_n\in A_n)=\prod^n_{k=1}P(X_k\in A_k)$$

則稱 $$X_1,X_2,\cdots,X_n$$ 是獨立的（independent）。

【定理 7】（變異數的加性）

假設 $$X_1,X_2,\cdots,X_n$$ 為 $$n$$ 個獨立的隨機變數，則有

$$var(X_1+X_2+\cdots+X_n)=var(X_1)+var(X_2)+\cdots+var(X_n)$$

丁、Markov不等式

在記述統計裡（見定理1），我們已介紹過Markov不等式，它是直觀顯明的，其重要性是作為推導 Chebyshev 不等式的基礎，而 Chebyshev 不等式又是推導弱大數法則的根據。現在我們用機率語言來重述。

【定理 8】（Markov 不等式）

假設 $$X\ge 0$$ 為一個隨機變數，則對任意 $$\varepsilon>0$$，恆有

$$\displaystyle P(X\ge\varepsilon)\le \frac{E(X)}{\varepsilon}~~~~~~~~~(3)$$

【證明】我們只證離散的情形

$$\begin{array}{ll}E(X)&=\sum\limits_{x_k\ge\varepsilon}x_kf(x_k)+\sum\limits_{x_k<\varepsilon}x_kf(x_k)\\&\ge\sum\limits_{x_k\ge\varepsilon}x_kf(x_k)\\&\ge\sum\limits_{x_k\ge\varepsilon}\varepsilon f(x_k)=\sum\limits_{x_k\ge\varepsilon}\varepsilon f(x_k)=\varepsilon P(X\ge \varepsilon)\end{array}$$

兩邊除以 $$\varepsilon$$ 就得 $$(3)$$ 式。連續的情形同理可證。

【註】$$(3)$$ 式表示期望值可以控制尾巴事件 $$(X\geq\varepsilon)$$ 的機率。

戊、Chebyshev不等式

【定理 9】（Chebyshev 不等式）

假設 $$X$$ 為一個隨機變數，另 $$\mu=E(X)$$、$$\sigma^2=var(X)$$，則對任意 $$\varepsilon>0$$，恆有

$$\displaystyle P(|X-\mu|\ge\varepsilon)\le\frac{\sigma^2}{\varepsilon^2}~~~~~~~~~(4)$$

【證明】

$$P(|X-\mu|\ge\varepsilon)=P[(X-\mu)^2\ge\varepsilon^2]$$ （簡單代數）

$$\le\displaystyle\frac{E(X-\mu)^2}{\varepsilon^2}=\frac{\sigma^2}{\varepsilon^2}$$ （由 Markov 不等式）

$$=\displaystyle\frac{\sigma^2}{\varepsilon^2}$$ （$$var(X)$$ 的定義）

連結：初等的機率論（9）什麼是機率與機率法則？

參考書目：

1. William Feller: An Introduction to Probability Theory and its Applications. Vol.1 John-Wiley & Sons, INC. Third Edition, 1967.
2. Sheldon M. Ross: A First Course in Probability. 8th Edition, Prentice Hall, 2009.
   （這兩本是公認的機率論入門絕佳的書。第一本是經典；第二本是比較晚近寫成的書，經常被拿來當作大學部「初等機率論」這門課的教科書。）
3. Kai Lai Chung: Elementary Probability Theory. Springer, 2004.
4. Hugh Gordon: Discrete Probability. Springer, 1997.
5. Eugene Lukacs: Probability and Mathematical Statistics. Academic Press, 1972.
6. David Stirzaker: Elementary Probability. Cambridge University Press, 1994.
7. Jim Pitman: Probability. Springer-Verlag, 1993.
8. Janos Galambos: Introductory Probability Theory. Marcel Dekker, INC. 1984.

註：通常要講述機率論必須用到「測度積分論」的數學工具，或至少要用到微積分。因此要為一般讀者介紹機率論的讀物誠屬不容易。上述八本書盡量壓低要用到的數學工具，大部分只需排列與組合，只有少部份要用到一點兒微積分。

從科學方法論的觀點來看，機率論與統計學是一體的兩面，機率論是「演繹法」，統計學是「歸納法」。因此，本文的主題雖然是機率論，但是也順便介紹一點點統計學的概念。