黃金比例Ⅰ(Golden Ratio Ⅰ)

黃金比例Ⅰ(Golden Ratio  Ⅰ)
國立蘭陽女中數學科陳敏晧老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要:本文首先定義黃金比例，接著介紹黃金比例與 等腰三角形的關係、黃金比例與黃金矩形的關係、黃金比例與等角螺線的關係、黃金比例與金字塔的關係。

歐幾里得(Euclid, ca.300B.C.)的《幾何原本》(Elements)是一部劃時代的著作，它偉大的歷史意義在於它是用公理法建立起演繹體系的最早典範。

《幾何原本》全書共13 卷。這本著作是現代數學的基礎，在西方僅次於《聖經》流傳最廣的書籍，書中內容第一卷至第六卷談論平面幾何；第七至九卷為數論內容；第十卷論無理數；第十一至十三卷以立體幾何為範疇。黃金比例，首先迂迴出現在《幾何原本》的卷二，其後在卷六有明確的定義：

一直線按中末比(extreme and mean ratio)分割的意思是說，
該直線的全長和分割後較長線段之比，等於較長線段和短線段之比。¹

如圖一所示，即 \(\overline{AB}:\overline{AC}=\overline{AC}:\overline{CB}\)，若假設 \(\overline{CB}=1\)，且 \(\overline{AC}=x\)，求 \(x=?\)

解法：因為 \(\overline{AB}:\overline{AC}=\overline{AC}:\overline{CB}\)，得 \((x+1):x=x:1\)，根據比例性質得 \(x^2=x+1\)，移項得 \(x^2-x-1=0\)，解得

\(\displaystyle x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot 1\cdot (-1)}}{2\times 1}=\frac{1\pm\sqrt{5}}{2}\)

因為 \(x>0\)，所以，取 \(x=\frac{1+\sqrt{5}}{2}\)

此比例(proportion)以符號 \(\Phi\) (phi)表示，值為 \(\frac{1+\sqrt{5}}{2}\) \(\approx{1.6180339887}…\)，我們稱此比值為黃金比例(Golden Ratio)，稱 \(C\) 點為 \(\overline{AB}\) 的黃金分割點(Golden Section Point)。

布魯克曼(Paul S. Bruckman)在1977 年於《費波納奇季刊(The Fibonacci Quanterly)》發表一首打油詩〈一成不變的中項〉(黃金比例有時也稱為黃金中項)：

黃金中項真無理，
它不是你那普普通通的無理數。
如果你把它倒過來(這真有趣！)，
你會得到它本身減一，
可是如果把它加一，
就得到了它的平方，
請相信我。²

附記：《幾何原本》最佳英譯本為希思(Thomas Little Heath, 1861-1940)的The thirteen books of Euclid’s Elements (1908 年初版；1926 年再版；1956 年新版)；中譯本可參考藍紀正、朱恩寬譯，梁宗巨、張毓新、徐伯謙校訂，《歐幾里得．幾何原本》，台北：九章出版社，1992。

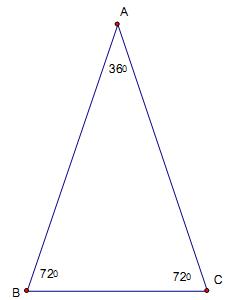
黃金比例與 \(36^\circ -72^\circ – 72^\circ\) 等腰三角形的關係

已知 \(\Delta ABC\) 為 \(36^\circ -72^\circ – 72^\circ\) 等腰三角形，如圖二所示，試問如何從幾何作圖中得到黃金比例，並證明之？

圖二：36度-72度-72度 等腰三角形圖。

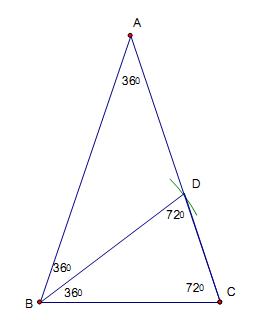
作法：以 \(B\) 點為圓心，\(\overline{BC}\) 為半徑劃弧，交 \(\overline{AC}\) 於 \(D\) 點，則 \(\frac{\overline{AD}}{\overline{DC}}\) 為黃金比例，\(D\) 點為 \(\overline{AC}\) 的黃金分割點，如圖三所示。

圖三： 36度-72度-72度 等腰三角形黃金分割點作圖。

證明：

因為 \(\overline{BC}=\overline{BD}\)，所以，\(\angle BDC=\angle C=72^\circ\)，得 \(\angle{DBC}=180^\circ -2\times 72^\circ =36^\circ\)，

則 \(\overline{AD}=\overline{BD}=\overline{BC}\) (因為兩底角相等)，又 \(\Delta ABC\backsim\Delta BDC\) (AA相似)，

得 \(\frac{\overline{AC}}{\overline{BC}}=\frac{\overline{BC}}{\overline{CD}}\)，轉換成 \(\frac{\overline{AC}}{\overline{AD}}=\frac{\overline{AD}}{\overline{CD}}\)，根據歐幾里得定義，\(\frac{\overline{AD}}{\overline{CD}}\) 為黃金比例，得證。

黃金比例與黃金矩形的關係

已知一個矩形的紙張裁去一個以矩形的寬為邊長的正方形，若剩下的矩形和原來的矩形相似，則此矩形的長和寬的比值？

解法:

圖四：黃金矩形分割圖。

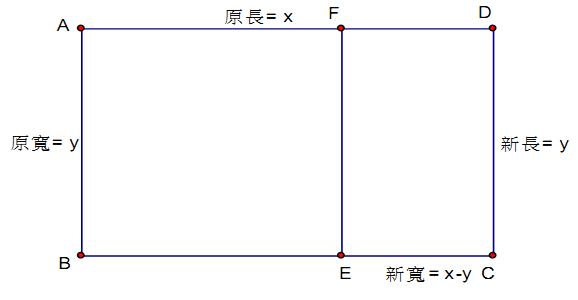
如圖四所示，因為 \(\Box ABCD\backsim\Box ECDF\)，

設矩形 \(ABCD\) 的原長 \(\overline{AD}=x\)，原寬 \(\overline{AB}=y\)，因為 \(\frac{\overline{AD}}{\overline{AB}}=\frac{\overline{CD}}{\overline{CE}}\)，則 \(\frac{x}{y}=\frac{y}{x-y}\)，

移項得 \(x^2-xy=y^2\)，即 \(x^2-xy-y^2=0\)，同除 \(y^2\)，得 \((\frac{x}{y})^2-(\frac{x}{y})-1=0\)，

代一元二次方程式公式解得 \(\frac{x}{y}=\frac{1+\sqrt{5}}{2}\)，此比值即是黃金比例，

若矩形的長寬比為黃金分割比值(Golden section ratio)，此矩形稱為黃金矩形。

民國九十年大學聯考社會組選擇題第一題出現黃金比值問題，如下所敘：

設實數 \(x=\frac{\sqrt{5}-1}{2}\)，下列哪些選項的值跟 \(x\) 相等？

\((\mathrm{A})~0.62\)
\((\mathrm{B})~\frac{1}{x}-1\)
\((\mathrm{C})~1-x^2\)
\((\mathrm{D})~\frac{1}{1+x}\)
\((\mathrm{E})~\)無窮級數 \(1-x+x^2-x^3+…+(-1)^nx^n+\cdots\) 之和

解法：

\((\mathrm{A})~\because x=\frac{\sqrt{5}-1}{2}\in Q’\)，但是 \(0.62\) 為有理數，錯誤。
\((\mathrm{B})~\)\(\begin{array}{ll}\frac{1}{x}-1&=\frac{1}{\frac{\sqrt{5}-1}{2}}-1=\frac{2}{\sqrt{5}-1}-\frac{\sqrt{5}-1}{\sqrt{5}-1}=\frac{(3-\sqrt{5})(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}\\&=\frac{2\sqrt{5}-2}{4}=\frac{\sqrt{5}-1}{2}=x\end{array}\)，正確。
\((\mathrm{C})~\)由 \((\mathrm{B})\) 知，因為 \(\frac{1}{x}-1=x\)，整理得 \(1-x=x^2\)，移項得 \(1-x^2=x\)，正確。
\((\mathrm{D})~\)由 \((\mathrm{C})\) 知，因為 \(1-x^2=x\)，整理得 \(1=x+x^2=x(1+x)\)，移項得 \(\frac{1}{1+x}=x\)，正確。
\((\mathrm{E})~\)利用無窮等比級數公式 \(1-x+x^2-x^3+…+(-1)^nx^n+\cdots=\frac{1}{1-(-x)}=\frac{1}{1+x}\)，正確。

因此正確答案為 \((\mathrm{B})(\mathrm{C})(\mathrm{D})(\mathrm{E})\)。

黃金比例與等角螺線的關係

圖五：等角螺線分割圖。

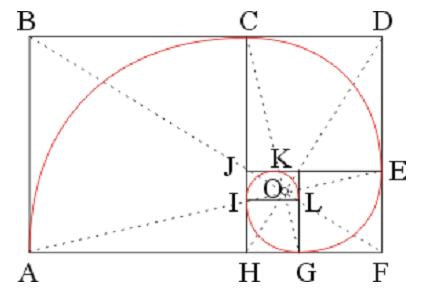
在圖五中，\(\Box ABDF, \Box CDFH, \Box EFHJ, \Box GHJK, \Box IJKL, …\)等都是黃金矩形，這些矩形中每兩個都相似（亦即：邊的比值相等），而且後一矩形都是由其前面的矩形挖掉一個正方形而得的。如：\(\Box CDFH\) 是由 \(\Box ABDF\) 挖掉正方形 \(\Box ABCH\) 而得的。

此時，上列矩形的第一個頂點  \(A\)、\(C\)、\(E\)、\(G\)、\(I\)、\(K…\)等會落在一等角螺線上，此等角螺線的極點是 \(\overline{AE},\overline{BF},\overline{CG},\overline{DH},…\)等共交的點 \(O\)。

若以 \(O\) 為極點，射線 \(\vec{OE}\) 為極軸，且 \(A\) 的極坐標為 \((a,\pi)\)，則此等角螺線的極坐標方程式為

\(\displaystyle r=\frac{a}{\phi^2}\left(\phi^{\frac{2}{\pi}}\right)^\theta\)

其中 \(\displaystyle\phi=\frac{1+\sqrt{5}}{2}\)。此等角螺線通常稱為黃金螺線。  ³

等角螺線(equiangular  spiral,  又稱對數螺線、生長螺線)，是由笛卡爾(René  Descartes,  1596-1650)在1638 年發現的，後來，雅各布．伯努利(Jakob Bernoulli ,1654-1705)後來重新研究之，他發現了等角螺線的許多特性，如等角螺線經過各種適當的變換之後仍是等角螺線，他十分驚嘆和欣賞等角螺線的特性，故要求死後將之刻在自己的墓碑上，並附詞「縱使改變，依然故我」(eadem  mutata  resurgo)，可惜雕刻師誤刻為阿基米德螺線。海洋生物中的等角螺線代表就是鸚鵡螺(又稱菊石)，如圖六所示，牠存於印度洋和太平洋海區，北至日本南方，南至大堡礁，西至安達曼海，東至斐濟等地區均有發現，由於生存年代久遠，科學家稱之為：「活化石」。

圖六：鸚鵡螺(又稱菊石)圖。 (註四)

國立臺灣師範大學數學系許志農教授在《高中數學珍寶》曾以對數螺線編寫一道數學問題：

「阿螺正在研究一個對數螺線。他從螺線中心畫出一條射線，該射線與螺線剛好交於六個點，離中心最近的點與中心距離 \(128\) 公分。更巧的是，這六個交點與中心的距離都是整數值，且都不超過 \(1000\) 公分。\((1)\) 問該螺線的公比? \((2)\) 問其餘五個點與中心的距離?  」⁵

黃金比例與金字塔的關係

馬丁．葛登能(Martin Gardner)在其《號稱科學的時尚熱及謬誤(Fads and Fallacies in the Names of Science)》中提到：「希羅多德(Herodotus, 485-425B.C.)說，金字塔(pyramid)在建造的時候，每一面的面積等於一個正方形的面積，而該正方形的邊長等於金字塔的高。」

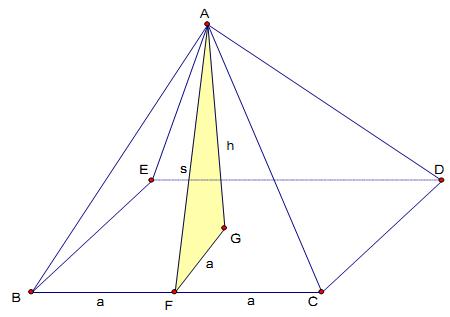
已知：\(A-BCDE\) 為金字塔，如圖七所示，若底面正方形邊長為 \(2a\)，且其高為 \(h\)，頂點 \(A\) 到底邊 \(\overline{BC}\) 為 \(s\)。

求證：\(\displaystyle\frac{s}{a}=\frac{1+\sqrt{5}}{2}\)

圖七：A-BCDE 為金字塔圖。

證明：

因為每一面的面積等於一個正方形的面積，且該正方形的邊長等於金字塔的高，

所以，\(a\Delta ABC=a\Box BCDE\)，即 \(\frac{1}{2}\cdot 2a\cdot s=(2a)^2\)，又 \(h=2a\)，代入得 \(h^2=a\cdot s\)，

根據畢氏定理得 \(h^2=s^2-a^2\)，即 \(as=s^2-a^2\)，同除以 \(a^2\) 得 \(\frac{s}{a}=(\frac{s}{a})^2-1\)，

移項得 \((\frac{s}{a})^2-(\frac{s}{a})-1=0\)，代入公式解得 \(\frac{s}{a}=\frac{1+\sqrt{5}}{2}\)

註：

1. 李維歐(Mario Livio)著、丘宏義譯，《黃金比例(The Golden Ratio)》，台北：遠流出版社，2004，頁21。
2. 李維歐(Mario Livio)著、丘宏義譯，《黃金比例(The Golden Ratio)》，頁110。
3. 趙文敏(1989)，〈等角螺線及其他(上)〉，《科學月刊》，第20 卷，第9 期，頁672-675；趙文敏(1989)，〈等角螺線及其他(下)〉，《科學月刊》，第20 卷，第10 期，頁774-776。
4. 陳柏亨、曾學仁、胡宗鳳／攝影。
5. 參考答案為 \((1)\) 公比為 \(\frac{3}{2}\)。\((2)\) 五個點依次為 \(192, 288, 432, 648, 972\)

連結：黃金比例Ⅱ

參考文獻

1. 李維歐(Mario Livio)著、丘宏義譯，《黃金比例(The Golden Ratio)》，台北：遠流出版社，2004 年。
2. 藍紀正、朱恩寬譯，梁宗巨、張毓新、徐伯謙校訂，《歐幾里得．幾何原本》，台北：九章出版社，1992 年。
3. 蔡聰明，《數學的發現趣談》，台北：三民書局，2000 年。