大數法則（4）弱大數法則（Weak law of large numbers）

Posted on 2011/09/23 in 數學, 機率統計 with 沒有迴響 26,873 views

大數法則（4）弱大數法則（Law of large numbers-4. Weak law of large numbers）
國立高雄大學應用數學系黃文璋教授/國立高雄大學應用數學系黃文璋教授責任編輯

摘要：本文從「伯努力試驗(Bernoulli trial)」談起，說明「大數法則」的主要內涵，進而介紹「弱大數法則(weak law of large numbers)」，並釐清常見的誤解。

大數法則又稱大數率或平均法則(law of averages)。由於有大數法則，使得在不確定性(uncertainty)中，我們仍能掌握一些確定性(certainty)；在混亂(chaos)中，仍有其秩序(order)。大數法則是說：若一實驗（或觀測），能持續且重複地進行，則觀測值之平均，將任意接近期望的成果。比較正式一點的說，就是隨機所產生樣本之平均，當樣品數很大，將有很大的機率，接近母體之平均。

機率論早期的發展，常對某件事是否發生有興趣。如：投擲銅板是否出現正面？玩撲克牌得到 \(3\) 條等。換句話說，對只有兩個結果的觀測有興趣。以 \(X_i=1\)，表第 \(i\) 次觀測該事件發生，\(X_i=0\)，表第 \(i\) 次觀測該事件未發生。如此觀測到一串 \(0,1\) 的數列。

這種數列，今日稱作伯努力數列(Bernoulli sequence)。而這類只有兩個結果的實驗，便稱作伯努力試驗(Bernoulli trial)。這是因瑞士數學家伯努力(Jacob Bernoulli,1654-1705)，最先探討而得名。在他死後八年，1713年，他姪兒尼古拉斯伯努力(Nicholas Bernoulli, 1687-1759)，替他出版那本可說是機率論最早的書籍 Ars Conjectandi（原文為拉丁文，英文書名為The Art of Conjecturing)。在這本書中，伯努力證明了一以他的姓為命名的定理，即伯努力法則(Bernoulli law)：

獨立且重複地觀測一發生機率為 \(p\) 之事件 \(A\)，
當觀測次數趨近至 \(\infty\)，事件發生之相對頻率接近 \(p\) 之機率，將趨近 \(1\)。

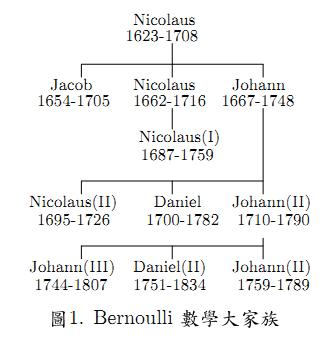
註一：Bernoulli一家可說是數學史上相當顯赫的一家。在三代裡，至少有八位，對數學、機率或統計有貢獻。其中有五位算是相當傑出。在數學、機率或統計中，常會見到Bernoulli，不見得是同一人。我們列出伯努力四代的部分成員於圖一。西方人的姓(last name)較少相同，名(First name)則很容易相同。

在同一領域出名且姓相同的，往往並不大多。所以我們通常以姓稱呼西方的科學家、文學家及藝術家等名人。如：牛頓、高斯及歐拉等，都是姓。而幾百年來也沒產生第二個科學家是牛頓、高斯及歐拉。若真有同姓的，再附上名，即可區隔。只是這套慣用的稱法，對Bernoulli就不適用了。由於這是一數學大家族，不但你見到的Bernoulli可能不是同一人，有幾位的名也相同。中國人對於取名，常會避長者諱。外國人則有時為小孩取某長者之名，以為紀念。這點在Bernoulli家族很明顯，還有取與自己同名的。圖一中有11人，卻只有4個不同的名。有時以二世(II)，三世(III)來區隔，有時也不區隔。

另一個Bernoulli家族的名會令人產生困擾的是，有幾位曾在歐洲幾個國家居住，而在不同的地方會有不同的名。以我們所提到的Bernoulli家族第一位數學家為例，Jacob有時寫成Jakob；他又稱為Jacques (有時寫成Jaques)；有時又稱為James。為了提昇機率與統計的發展，1975年還成立了一個伯努力協會(Bernoulli Society)的國際組織，可見伯努力家族在機率與統計界的被重視。

伯努力所指的『趨近』是什麼意思呢？

令 \(n(A)\) 表觀測 \(n\) 次，事件 \(A\) 所發生之次數。又以 \(p_{n,k}\) 表 \(n(A)=k\) 之機率，則

\((1)~~~p_{n,k}=P(n(A)=k)=\dbinom{n}{k}p^k(1-p)^{n-k},~~~k=0,1,…,n\)

當 \(n\) 很大時，事件 \(A\) 發生之相對頻率 \(n(A)/n\) 與 \(p\) 之差距不應太大。但 \(n(A)\) 可能每回觀測都不盡相同，畢竟這是一隨機現象。有時 \(n(A)=n\)，有時 \(n(A)=0\)。我們上一節才討論巨數法則。投擲一公正銅板 \(100\) 次，\(100\) 次全出現正面的機率當然很低，僅 \(1/2^{100}\)。但若一直重複做這件事(每回投擲 \(100\) 個銅板)，譬如說做了 \(2^{100}\) 回，則其中出現一回 \(100\) 個全是正面，就不用太奇怪。如果回數再多些，譬如做了 \(2^{110}\) 回，就更容易出現好幾回 \(100\) 個全部是正面了。因平均可出現 \(2^{110}/2^{100}=2^{10}=1,024\)(次)。

註二：要完成 \(2^{100}\) 回投擲銅板 \(100\) 次，其實並非易事。假設以電腦模擬，且 \(1\) 秒鐘可模擬 \(1\) 萬兆\((=2^{16})\) 回，夠快了吧! \(1\) 天有 \(86,400\) 秒，\(1\) 年 \(365\) 天約有 \(3.1536\times 10^7\) 秒。因此一年約可模擬 \(3.1536\times 10^{23}\) 回。又 \(2^{100}\) 約等於 \(1.2676506\times 10^{30}\)，兩者相除，得到約要模擬 \(4.01969\times 10^6\) 年。要四百多萬年才能模擬完，中華民族才號稱有五千年文化。野史裡偶有投擲出 \(100\) 個正面的紀載，宋朝名將狄青曾辦到，見黃文璋(2003)p.71，那些銅板當然都是特製的。如果銅板為公正，你現在知道了，投擲 \(100\) 個，是很難出現 \(100\) 個全是正面。若想靠多投擲幾回而得，幾回之多，乃遠超乎我們所能想像。

對於隨機現象的種種解釋，自然須以機率為依歸。伯努力是認為 \(n(A)/n\) 與 \(p\) 之差是『不太可能』過大。即只要 \(n\) 夠大，\(|\frac{n(A)}{n}-p|>\varepsilon\) 之機率應很小，其中 \(\varepsilon\) 為任一正數。而此機率為

\((2)~~~\displaystyle\sum_{|(k/n)-p|>\varepsilon}p_{n,k}=\sum_{|(k/n)-p|>\varepsilon}\dbinom{n}{k}p^k(1-p)^{n-k}\)

伯努力辛苦證明

\((3)~~~\displaystyle\lim_{n\to\infty}\sum_{|(k/n)-p|>\varepsilon}\dbinom{n}{k}p^k(1-p)^{n-k}=0\)

其中的求和當然不會是容易的工作。今日已少有人看過(可能也不想，甚至不知道)他的證法。有興趣的讀者，可參考Renyi(1970)pp.195-196。事實上，利用柴比雪夫不等式(Chebyshev inequality, Pafnuty L. Chebyshev, 1821-1894, 為俄國著名數學家)，可輕易證出比伯努力更一般的結果，可參考黃文璋(2010)p.124。

伯努力所指的事件發生之相對頻率，其實就是

\(\displaystyle f_n(A)=\frac{n(A)}{n}=\frac{X_1+\cdots+X_n}{n},~~n\ge 1\)

其中 \(X_1,\cdots,X_n\) 為獨立且有相同分佈(independent and identically distributed, 簡稱 \(\mathrm{iid}\))之隨機變數，\(X_i\) 取值 \(0\) 或 \(1\)，且 \(P(X_i=1)=p,~i\ge 1\)。隨機變數只取值 \(0\) 或 \(1\)，且取值 \(1\) 的機率為 \(p\)，便稱為有參數 \(p\) 之伯努力分佈(Bernoulli distribution)，以 \(\mathrm{Ber}(p)\) 表之。

伯努力即指出，\(\mathrm{iid}\) 的隨機變數 \(X_i, i\ge 1\)，以 \(\mathrm{Ber}(p)\) 為共同分佈時，當 \(n\to\infty\) 時，\((X_1+\cdots+X_n)/n\) 會偏離 \(p\) 『太遠』(如差距超過 \(\varepsilon\))的機率趨近至 \(0\)。

讀者可看出大數法則與巨數法則是兩個不同的法則。曾在網路上一篇文章中，看到底下一段話：

記得保險業有一條『大數法則』，意思是只要大量客人，十位或一百位或一千位，總有一位客人投保。換句話說，你失敗，只是個人不夠勤力，接觸的客人不夠多之故。

其實這應是巨數法則，而非大數法則。對一事件 \(A\) 當觀測數 \(n\) 很大，巨數法則關心 \(A\) 是否發生，大數法則則是說事件 \(A\) 發生的總次數 \(n(A)\)，『約』是 \(np\)，其中 \(p\) 為 \(A\) 發生的機率。也可以這麼說，大數法則是比巨數法則更精確的法則。它指出當觀測數 \(n\) 很大，一特定事件大約發生多少次。因 \(n\) 很大時，事件 \(A\) 約發生 \(np\) 次，即使 \(p\) 很小，只要 \(np>1\)，則看到事件 \(A\) 發生，就不足為奇。而這就是巨數法則所指出的現象。

大數法則可以支持頻率對機率的解釋。設有一銅板，出現正面的機率為 \(p\)(或一事件發生的機率為 \(p\))，只投擲一次，不是正面就是反面，無法感受 \(p\) 的意義。但只要投擲數夠大，銅板出現正面的相對頻率，就有可能接近 \(p\) 了。伯努力之後，機率學家們，繼續探討大數法則。1928年，俄國機率學家辛欽(Aleksandr, Y. Khinchin, 1894-1959)，證明對 \(\mathrm{iid}\) 的隨機變數，只要期望值存在，不論分佈為何，大數法則便成立。即

對 \(\forall n\ge 1\)，設 \(X_1,\cdots,X_n\) 為 \(\mathrm{iid}\) 之隨機變數，

且設 \(E(X_1)\) 存在 (即 \(-\infty<E(X_1)<\infty\))，則樣品平均(sample mean)

\(\displaystyle \overline{X}_n=\frac{X_1+\cdots+X_n}{n},~~~n\ge 1\)

當 \(n\to \infty\) 時，會機率收斂(converges in probability) 至 \(E(X_1)\)，以

\((4)~~~\displaystyle \overline{X}_n \xrightarrow[n\to\infty]{P} E(X_1)\) 表之。

在此，機率收斂的定義如下：

定義1. 設有一數列之隨機變數 \(\{Y_n,~~n\ge 1\}\)，及一隨機變數 \(Y\)，若

\((5)~~~\displaystyle\lim_{n\to\infty} P(|Y_n-Y|>\varepsilon)=0,~\forall \varepsilon>0\)

則稱 \(n\to\infty\) 時，\(\{Y_n,~n\ge 1\}\)，機率收斂至 \(Y\)，且以 \(\displaystyle Y_n\xrightarrow[n\to\infty]{P} Y\) 表之。

\((5)\) 式是說，對 \(\forall \varepsilon>0\)，當 \(n\to\infty\) 時，\(|Y_n-Y|>\varepsilon\) 之機率趨近至 \(0\)。

亦即 \(|Y_n-Y|\le \varepsilon\) 之機率趨近至 \(1\)：

\((6)~~~\displaystyle\lim_{n\to\infty} P(|Y_n-Y|\le\varepsilon)=1,~\forall \varepsilon>0\)

辛欽所證出的結果，後來被稱為弱大數法則。當 \(\mathrm{iid}\) 的隨機數列 \(X_n, n\geq 1\)，只取 \(0,1\) 兩個值，且 \(P(X_1=1)=p\)，則 \(E(X_1)=p\)，這時，弱大數法則就回到伯努力版本。

弱大數法則並無法保證 \(n\) 很大時，樣本平均 \(\overline{X}_n\) 與隨機變數之期望值 \(E(X_1)\) 『必會』很接近。這與常數數列的收斂大不相同。對於隨機現象，所有的保證，都是機率式的。即弱大數法則保證 \(n\) 很大時，樣本平均 \(\overline{X}_n\) 與隨機變數之期望值 \(E(X_1)\) 很接近的機率很大。

不論 \(\overline{X}_n\) 與 \(E(X_1)\) 之差距要多小(譬如說 \(|\overline{X}_n-E(X_1)|\leq\varepsilon\)，其中 \(\varepsilon\) 可為一任一正數)此機率要多大(譬如說 \(P(|\overline{X}_n-E(X_1)|\leq\varepsilon)\) 大於 \(1-\delta\)，其中 \(\delta\) 可為任一正數。)，皆能辦到，只要樣本數夠大。即對每一 \(\varepsilon>0\) 及 \(0<\delta<1\)，存在一 \(n_0\geq 1\)，使得

\((7)~~~P(|\overline{X}_n-E(X_1)|\le \varepsilon)>1-\delta\)，當 \(n\ge n_0\)

或等價地說

\((8)~~~\displaystyle\lim_{n\to\infty} P(|\overline{X}_n-E(X_1)|\le \varepsilon)=1,~\forall \varepsilon>0\)

弱大數法則並沒有說，\(n\) 很大時，\(X_n\) 會等於 \(E(X_1)\)。很多初學者會誤以為如此，但這是錯的。即使 \(n\) 很大時，\(|\overline{X}_n-E(X_1)|\) 必很小，此說法也是錯的。這些皆非機率式的說法。

正確的說法是當 \(n\) 很大時，\(|\overline{X}_n-E(X_1)|\) 很小的機率會很大。以數學式子表示就是 \((7)\) 式或 \((8)\) 式。對於隨機現象，我們通常只能做機率式的保證。初學者或許會以為，我們的保證好似都有些保留，不像數學中一向斬釘截鐵似的說法有權威。但這就是機率與數學之別：看似不確定，其實是更可靠的保證。只要想甲醫生肯定地說這病人活不過 \(3\) 個月，乙醫生說病人活不過 \(3\) 個月的機率為 \(0.99\)，你覺得哪一種講法較精準？

弱大數法則不只針對 \(\mathrm{iid}\) 的隨機變數才成立，條件可放寬些。歷來機率學家給出不同條件下的弱大數法則，使其適用範圍更廣。

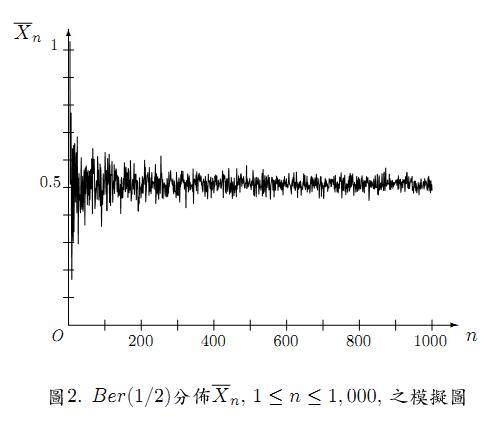
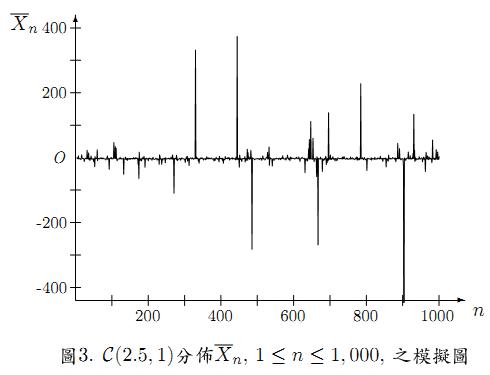
大數法則針對期望值存在的隨機變數，期望值若不存在，像是柯西分佈(Cauchy distribution)，就不適用了。圖2給出當 \(X_n,n\geq 1\)，為 \(\mathrm{iid}\) 之隨機變數，且以 \(\mathrm{Ber}(1/2)\) 為共同分佈，\(\overline{X}_n\) 之一模擬圖形，\(1\leq n\leq 1,000\)。可看出除了 \(n\) 不太大時，\(\overline{X}_n\) 與 \(0.5\) 有較大差距，之後就與 \(0.5\) 很接近了。對參數 \(2.5\) 及 \(1\) 之柯西分佈，以 \(\mathrm{C}(2.5,1)\) 表之，即機率密度為

\(\displaystyle f(x)=\frac{1}{\pi(1+(x-2.5)^2)},~~~x\in\mathbb{R}\)

圖3給出 \(\overline{X}_n\) 之模擬圖形。由於此分佈之期望值不存在，大數法則不適用，圖形顯示 \(\overline{X}_n\) 震盪很大。

在統計裡，很多不錯的統計方法，都基於大數法則。著名的動差估計法(metho d of moment estimator)為一例。設隨機變數 \(X\) 有參數 \(\lambda\) 之波松分佈(Poisson distribution)，以 \(X\)~\(P(\lambda)\) 表之，\(\lambda >0\)。即 \(X\) 之機率密度函數為

\(\displaystyle f(x)=\frac{e^{-\lambda}\lambda^x}{x!},~~~x=0,1,\cdots\)

我們想要估計 \(\lambda\)，獨立且重複地觀測 \(n\) 次，得到樣本 \(X_1,…,X_n\)。則可利用樣本平均 \(\overline{X}_n\) 作為 \(\lambda\) 的估計量，即為動差估計法。由於 \(E(X)=\lambda\) 恰為 \(X\) 之期望值，此略可說明何以動差估計法通常是不錯的估計量。因至少我們確定取樣夠多時，它接近欲估計的參數之機率便很大。

我們常會接觸到機率為 \(0\) 之事件。自區間 \([0.1]\) 隨機取一個點，會取中 \(0.3\) 的機率為何？\(0\)，你可能會不假思索地回答。你還知道任何一點被取中之機率為 \(0\)。如果令 \(X\) 表取中之點，則 \(X\) 為一連續型的機率變數。因此 \(X\) 會等於 \([0,1]\) 間任一數之機率皆為 \(0\)。修過機率與統計的課程，使你具備基本的機率知識，但有人一取之下，取中 \(0.729\)，他問妳機率不是 \(0\) 嗎？怎麼卻發生了？

要知機率 \(0\) 的事件，不代表不會發生，使現象常讓初學者感到迷惑。事實上，事件之『不會發生』、『會發生』及『一定發生』等，皆非專業的說法。專業的說法分別是：機率為 \(0\)，機率為正，機率為 \(1\)。有人取中 \(0.729\)，他懷疑 \(0.729\) 被取中的機率其實大於 \(0\)。如何跟她解釋？

此時，大數法則便可派上用場。你請他再取 \(1\) 次，第 \(3\) 次取，繼續取，依序取了 \(n\) 次，如此得到隨機數列 \(X_1,\cdots,X_n\)，其中 \(X_i=1\)，表第 \(i\) 次取中 \(0.729\)，\(X_i=0\)，表第 \(i\) 次未取中 \(0.729,~i\geq 1\)。然後算出 \(0.729\) 出現次數的相對頻率，即求

\(\displaystyle \overline{X}_n=\frac{X_1+\cdots+X_n}{n},~~~n\ge 1\)

雖然 \(X_1=1\)，但自 \(X_2\) 起，應都是 \(0\) 了。隨著 \(n\) 增大，\(\overline{X}_n\) 愈來愈接近 \(0\)。

何以我們那麼『確定』？因弱大數法則告訴我們 \(n\rightarrow\infty\) 時

\(\overline{X}_n \xrightarrow[n\to\infty]{P} E(X_1)=0\)

由於上述這種困擾，有時機率學家，傾向以幾乎不可能(almost impossible)及幾乎確定(almost certain)，來取代『不可能』(不會)及『確定』(必會)。

附帶一提，當有人告訴你，他自區間 \([0,1]\) 隨機地取一個點，取中 \(0.729\)，你可大膽地請問他，是否真的是 \(0.729\)？你的量尺夠精確嗎？為何你如此有信心，該數可能是因量測不夠精確，才以為是 \(0.729\)，其實並不是 \(0.729\)？此因 \([0,1]\) 間有理數的集合是可數的(countable)，而可數集合之勒貝格測度(Lebesgue measure)為 \(0\)， \([0,1]\) 間無理數之勒貝格測度為 \(1\)。因此隨機取一點，會取中無理數的機率為 \(1\)。我們當然寧可認為是因他沒量精準，才以為得到的是有理數。

最後，隨機變數的不獨立，或分佈不同，在適當條件下，弱大數法則仍會成立。可參考黃文璋(2010)5.3節。

連結：大數法則（5）強大數法則

參考文獻：

黃文璋(1999)，數學欣賞。華泰文化事業股份有限公司，台北。
黃文璋(2003)，隨機思考論。華泰文化事業股份有限公司，台北。
黃文璋(2010)，機率論，第二版。華泰文化事業股份有限公司，台北。
Chung K. L. (2001). A Course in Probability Theory, 3rd ed, Academic Press, New York
Diaconis, P. and Mosteller, F. (1989). Method for studying coincidences. Journal of the AmericanStatistical Association, 84, 853-861
Littlewood J.E.(1953). A Mathematican’s Misscellany. Methuen, London.
Renyi, A.(1970). Foundations of Probability . Holden-Day, Inc., San Francisco.
Shermer, M.(2003). Co dified claptrap. Scientific American , June ,288(6), 35.
Shermer, M.(2004). Miracle on probability street. Scientific American , August, 291(2), 32.