輾轉相除法(I) (Euclidean algorithm)

輾轉相除法(I) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師

歷史溯源：歐幾里得(Euclid,ca.325BC-ca.265BC)(如右圖)的《幾何原本(Elements)》第七卷的第一、二個命題論述如何用輾轉相除法求兩整數的最大公因數，因此，輾轉相除法又稱歐幾里得算法。

狄里克利(Peter Gustav Lejeune Dirichlet, 1805-1859)在他的《數論》一書中說「本書的整個結構奠定在一塊基石上面，即計算兩個整數的最大公因數(輾轉相除法)。」利用這個方法，可以較快地求出兩個自然數的最大公因數，稱為 g.c.d.(greatest common divisior)^[1]。 所謂最大公因數，是指幾個數的共有的因數之中最大的一個，例如：8和12的最大公因數是4，記作 g.c.d.(8,12)=4。

已知：$$a,b\in \mathbb{N}$$，且 $$a=bq+r$$，其中 $$q,r\in \mathbb{Z}$$，$$0\le r <b$$

求證：$$(a,b) = (b,r)$$。

證明：令 $$(a,b)=d_1$$, $$(b,r)=d_2$$

$$(1)~\because (a,b)=d_1$$，則 $${d_1}\left| a \right.$$ 且 $${d_1}\left| b \right.$$，$$\therefore \exists 1,q\in \mathbb{Z}$$，
得 $$r=a-bq=a\times 1-b\times q$$，$$\therefore {d_1}\left| r\right.$$，即 $${d_1}\left| (b,r) \right.$$，$$\therefore {d_1}\left| d_2 \right.$$。

$$(2)~\because (b,r)=d_2$$，則 $${d_2}\left| b \right.$$ 且 $${d_2}\left| r \right.$$，$$\therefore \exists q,1\in \mathbb{Z}$$，
得 $$a=bq+r=b\times q+r\times 1$$，$$\therefore {d_2}\left| a\right.$$，即 $${d_2}\left| (a,b) \right.$$，$$\therefore {d_2}\left| d_1 \right.$$。

$$(3)~{d_1}\left| d_2 \right.$$ 且 $${d_2}\left| d_1 \right.$$，又 $$d_1>0$$，$$d_2>0$$ (最大公因數必為正數)，
因此，$$d_1=d_2$$，即 $$(a,b)=(b,r)$$。

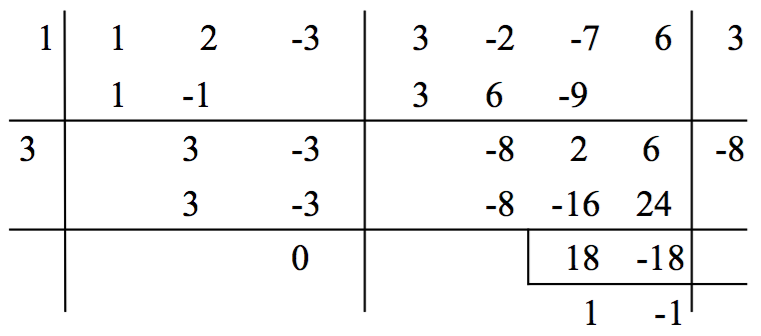
例題：求多項式 $$f(x)=x^2+2x-3$$ 與 $$g(x)=3x^3-2x^2-7x+6$$ 的最高公因式(H.C.F.)=                   。

參考解法：利用分離係數法。

即 $$\mathrm{H.C.F.}=x-1$$。

延伸性質：

1. 若 $$a,b\in\mathbb{N}$$，則 $$[a,b]=\frac{ab}{(a,b)}$$
2. 若 $$f(x),~g(x),~q(x),~r(x)$$ 為多項式，且 $$f(x)=g(x)q(x)+r(x)$$，則 $$\left( {f\left( x \right),g\left( x \right)} \right) = \left( {g\left( x \right),r\left( x \right)} \right)$$

數學遊戲：小蘭、小珍和小布午後玩遊戲，大姊小蘭的 $$A$$ 容器為 $$27$$ 毫公升，二姐小珍的 $$B$$ 容器為 $$15$$ 毫公升，小妹小布拿出 $$100$$ 毫公升的 $$C$$ 容器，問如何借用 $$A$$、$$B$$、$$C$$ 容器倒出 $$6$$ 毫公升的水？

參考解法：因為 $$(27,15) =3$$，則 $$3=15\times 2 – 27$$ ，因此 $$6=15\times 4 – 27\times 2$$。所以，先將 $$15$$ 毫公升的容器裝滿四次倒入 $$100$$ 毫公升的空容器中，再往 $$27$$毫公升的容器倒出兩次滿，則剩下的水就是 $$6$$ 毫公升。

最後，西方的歐幾里得利用更相減損的運算來求得兩數的最大公因數，對照中國，南宋數學家秦九韶(1202-1261)於其大作《數書九章》中有次序及有步驟地解出兩數的最大公因數，利用的方式仍然是輾轉相減法，此方法稱為「大衍求一數」，數學界稱為「中國剩餘定理(Chinese Remainder Theorem)」。

總之，輾轉相除法看似只是一種運算方法，但是，其背後蘊含深厚的數學內容，例如：給定一個實數 $$\alpha~(\alpha>0)$$，找出一個有理數 $$\frac{q}{p}$$ 去逼近它，使 $$\left| {\alpha- \frac{q}{p}} \right|$$ 為最小，這是一個重要的數學問題，也就是數學史上的丟番圖(Diophantine)逼近論，換言之，就是以有理數逼近實數，方法即先以輾轉相除法求得連分數，然後不斷接近實數，如祖沖之的約率 $$\frac{22}{7}$$和密率 $$\frac{355}{113}$$，就是企圖以有理數逼近圓周率 。

[註1] 在多項式中稱為最高公因式，以符號H.C.F(highest common factor)表示。

連結：輾轉相除法(II)

參考資料：

1. 蔡聰明，《數學的發現趣談》，台北：三民書局，2000年。
2. 華羅庚，《與中學生談中國數學史上的幾大成就》，台北：九章出版社，2000年。