獨立事件 (Indenpent Event)

獨立事件 (Indenpent Event)
國立蘭陽女中陳敏晧教師

已知 \(A\) 與 \(B\) 為樣本空間中的兩個事件，

若 \(P(A\cap B)=P(A)\cdot P(B)\)，則稱 \(A\) 事件與 \(B\) 為獨立事件；
若 \(P(A\cap B)\ne P(A)\cdot P(B)\)，則稱 \(A\) 事件與 \(B\) 為相關事件。

另一種解釋獨立事件的方式為當 \(B\) 事件的發生並不影響事件 \(A\) 發生的機率，
即 \(P\left( {A\left| B \right.} \right) = P\left( A \right) \Leftrightarrow \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( A \right) \Leftrightarrow P\left( {A \cap B} \right) = P\left( A \right)P\left( B \right)\)。

若已知事件 \(A\) 與 \(B\) 為獨立事件，則

1. \(A\) 與 \(B’\) 為獨立事件。其中 \(B’\) 為之補集合。
2. \(A’\) 與 \(A\) 為獨立事件。
3. \(A’\) 與 \(B’\) 為獨立事件。

證明：

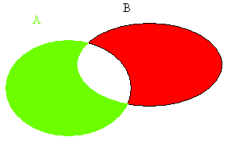
(1) \(\begin{array}{ll}P\left( {A \cap B’} \right) &= P\left( A \right) – P\left( {A \cap B} \right) = P\left( A \right) – P\left( A \right)P\left( B \right) \\&= P\left( A \right) \cdot \left( {1 – P\left( B \right)} \right) = P\left( A \right)P\left( {B’} \right)\end{array}\)，得證。參閱圖一。

圖一

(2) 的證明與(1)相同。

(3) \(\begin{array}{ll}P\left( {A’ \cap B’} \right) &= 1 – P\left( {A \cup B} \right) = 1 – P\left( A \right) – P\left( B \right) + P\left( {A \cap B} \right) \\&= 1 – P\left( A \right) – P\left( B \right) + P\left( A \right)P\left( B \right) \\&= \left( {1 – P\left( A \right)} \right) \cdot \left( {1 – P\left( B \right)} \right) = P\left( {A’} \right) \cdot P\left( {B’} \right)\end{array}\)

學習獨立事件時，應該理解其與互斥事件的關連性。

首先，定義互斥事件，若兩事件為互斥事件時，則 \(A\cap B=\varnothing\) ，
即 \(P(A\cap B)=P(\varnothing)=0\)。
因此，顯而易見若兩個非空事件 \(A\) 與 \(B\) 為互斥事件時，則事件 \(A\) 與 \(B\) 一定不是獨立事件。

另一個重點是獨立事件與期望值(Expected value，代號為 \(E\))的關係，若 \(X\) 與 \(Y\) 為兩個事件，則其期望值具有線性關係，即 \(E(aX+bY)=aE(X)+bE(Y)\)，其中 \(a\) 與 \(b\) 為兩個常數。但是，若 \(X\) 與 \(Y\) 彼此為獨立事件時，除了線性關性外，還具有 \(E(XY)=E(X)E(Y)\)，
說明如下：
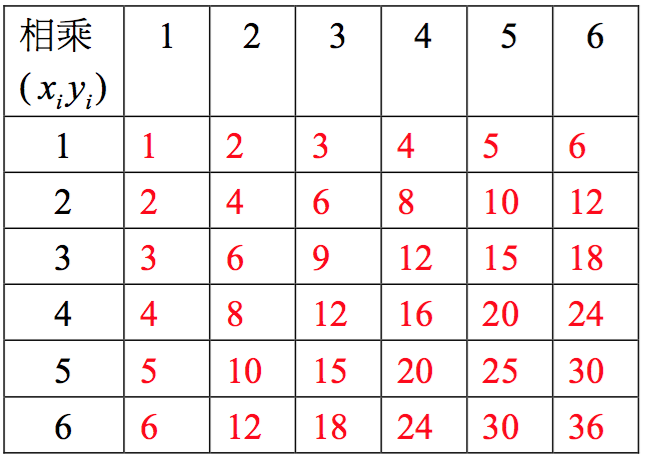
若 \(x_i\) 代表第一次擲骰子所出現的點數，\(y_i\) 代表第二次擲骰子所出現的點數，
所以，\({x_i},{y_i} \in \left\{ {1,2,3,4,5,6} \right\}\)，若已知 \(x_i\) 與 \(y_i\) 為獨立事件。

\(\displaystyle\begin{array}{ll}E\left( {XY} \right) &= \sum {{x_i}{y_i}{p_i}}\\&=\frac{1}{{36}}(1 + 4 + 6 + 12 + 10 + 24 + 16 + 9 + 20 + 48 + 30 + 16 + 36 + 40 + 48 + 25 + 60 + 36)\\&=\frac{1}{36}\times 441 = \frac{49}{4}\end{array}\)

\(\displaystyle\begin{array}{ll}E\left( X \right)E(Y) &= (\sum\limits_{i = 1}^6 {{x_i}{p_i}} )(\sum\limits_{i = 1}^6 {{y_i}{p_i}} )\\&=\left( {1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6}} \right) \cdot \left( {1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6}} \right)\\&= \frac{{1 + 2 + 3 + 4 + 5 + 6}}{6} \times \frac{{1 + 2 + 3 + 4 + 5 + 6}}{6}\\&=\frac{7}{2}\times\frac{7}{2}=\frac{49}{4}\end{array}\)

因此，若事件 \(X\) 與 \(Y\) 為獨立事件時，則 \(E(XY)=E(X)E(Y)\) 。

根據加拿大安大略所出版《資料管理中的數學（Mathematics of Data Management）》中提及一個有趣的問題：An airplane can make a safe landing if at least half of its engines are working properly. Suppose that engine failures are independent events. Determine whether a two-engine plane is safer than a four-engine plane if the chance that an engine fails is 1 in 2.

題意：一架飛機能夠安全降落的前提是至少它的一半引擎是能夠順利運作的，假設每個引擎間的運作都是獨立事件，如果每個引擎失敗運作的機率為二分之一，請確定一架有兩個引擎的飛機是比有四個引擎的飛機安全。

解法：設有二個引擎飛機安全降落機率為 \(A\)，設有四個引擎飛機安全降落機率為 \(B\)。

\(P\left( A \right) = {\left( {\frac{1}{2}} \right)^2} + C_1^2 \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{4} = \frac{{12}}{{16}}\)

\(P\left( B \right) = {\left( {\frac{1}{2}} \right)^4} + C_3^4{\left( {\frac{1}{2}} \right)^3} \cdot \frac{1}{2} + C_2^4{\left( {\frac{1}{2}} \right)^2} \cdot {\left( {\frac{1}{2}} \right)^2} = \frac{{11}}{{16}}\)，所以，\(P(A)>P(B)\)。

參考資料：

• Papoulis, A. (1984), Probability, Random Variables, and Stochastic Processes, New York: McGraw-Hill, p. pp. 139-152 .
• http://en.wikipedia.org/wiki/Independence_(probability_theory).