標準差

標準差 (Standard Deviation)
臺北市立和平高中黃俊瑋教師

給定一筆資料 \(x_1\)、\(x_2\)、\(\cdots\)、\(x_n\)，算術平均數 \(\mu=\frac{\sum_{i=1}^{n}x_i}{n}\) 一般用作為數據的代表值或衡量數據集中趨勢的統計量。雖然，算術平均數是數據重要代表值，但是可能發生下列情況：甲班與乙班某次數學考試的平均數皆為 \(50\) 分，但甲班同學的成績皆分佈在 \(40-60\) 分之間，而乙班約一半的學生都是 \(90\) 分以上，另一半學生都是個位數。這樣來看，這兩班的成績雖有相同的「中心」，即算術平均數，但它們整體的分散、分佈、變異情況大不相同。此時「\(50\) 分」這個數字之於兩班成績的意義以及可解釋數據的程度亦不同。

因此，統計學家進一步發展出衡量數據分散、變異情況的統計量。國中階段介紹了全距或四分位距，然讀者或許會覺得，這兩種統計量皆僅使用了「\(2\)」個數值來衡量整體數據的分散情況，所能提供的訊息有限。然而，該如何完整地用上 \(x_1\)、\(x_2\)、\(\cdots\)、\(x_n\) 這 \(n\) 筆資料來設計出更適當的統計量呢？

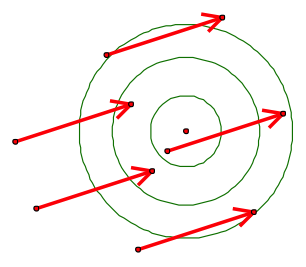
我們想像射箭比賽，參賽選手射出的各隻箭若離靶中心越接近，表示偏差越小，較集中，表現越穩定，越符合神射手的形象（如圖一所示）。反之，若所射各隻箭偏離中心很遠，較分散，即表現不穩定且偏差大（如圖二所示）。

圖一 各隻箭離中心近，較集中

圖二 各隻箭離中心較遠，較分散

依此射箭與靶心所得到的靈感，我們進一步利用每一筆數據與「中心」間的分散情況來建立新統計量。首先，如何定位這筆數據的中心呢？直觀地，大家會聯想到利用算術平均數作為中心，接著，我們開始評估各數據和中心間的差異。

首先，可能想到各數據與中心之差（離均差），然而，\(\displaystyle\frac{\sum_{i=1}^{n}(x_i-\mu)}{n}=0\)，

意即所有數據之離均差和為 \(0\)，此統計量無用。

再者，讀者可能會想到，利用各數據與中心之「距離」，即加上絕對值的方式來處理。

如此一來，可得一新的統計量：\(\displaystyle\frac{\sum_{i=1}^{n}|x_i-\mu|}{n}\)，

此統計量的意義即為各數據與中心（平均數）之距離的平均值，故簡稱為平均絕對離差。

然而，絕對值在相關理論推廣與計算上皆較不容易且麻煩（去絕對值需考慮正負或分段討論），特別是絕對值函數無法直接微分，因此，此統計量亦不用。

為了保持各項「皆正」的效果，這時統計學家想到了「平方」，

如此可造出新統計量 \(\displaystyle\frac{\sum_{i=1}^{n}(x_i-\mu)^2}{n}\)，並稱之為變異數。

變異數的意義可看成各數據與中心距離平方的平均值。

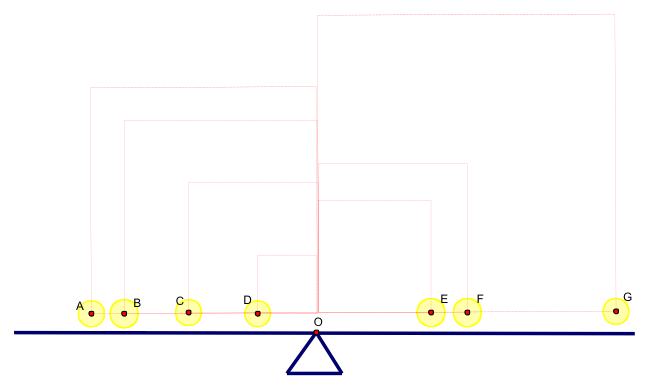
如圖三所示，中心平衡點為 \(A\)、\(B\)、\(C\)、\(D\)、\(E\)、\(F\)、\(G\) 七筆數據之算術平均數。利用各筆數據與平均數可造出正方形，而變異數的幾何意義則是圖三中各各個正方形面積的平均值。

然此變異數因平方後，數值放大效果或單位平方等因素為其缺點，因此，統計上我們常用的統計量為變異數的正平方根，即 \(\text{S.D}=\displaystyle\sqrt{\frac{\sum_{i=1}^{n}(x_i-\mu)^2}{n}}\)，此即為標準差（一般教科書會使用 \(\sigma\) 符號代表標準差）。而此標準差公式，一方面兼顧了數據中各個資料點，也考量了資料中心點，它也是統計上用來衡量數據分散、變異情況時，最常用且重要的統計量。

圖三　變異數的幾何意義

另一方面，就上述圖三中 \(A\)、\(B\)、\(C\)、\(D\)、\(E\)、\(F\)、\(G\) 這七筆數據的標準差來看，其幾何意義即是「以圖中這些正方形面積平均值為面積的正方形邊長」。一般而言，即是利用 \(n\) 筆數據與資料中心點─算術平均數─造出 \(n\) 個正方形，再求其平均面積，得一個「平均正方形」，再求其邊長得「平均邊長」，此值即為標準差。

在統計公式複雜且難記之餘，利用幾何上的直觀意義與想法，恰可提供一般讀者與中學生另類的記憶方式以及對複雜公式的數感。