二項式定理的推廣(二): 有理數冪次
二項式定理的推廣(二):有理數冪次
(The generalization of Binomial theorem(II):rational power)
臺北市立和平高中黃俊瑋教師
前文〈二項式定理的推廣(一):負整數冪次〉裡,對二項式定理作了冪次上的推廣,從正整數推廣至負整數。接著,我們進行另一個推廣:有理數冪次。不過,受限於篇幅,這裡主要先討論指數為 $$1/2$$ 次方的二項展開式。並同樣借用江戶時期日本數學家的方法來作說明。
首先,指數為 $$1/2$$ 次方的二項展開式與開平方問題為一體兩面,例如 $$(1+a)^{\frac{1}{2}}$$ 可看成 $$\sqrt{1+a}$$。再者,在東方數學史發展的過程裡,$$\sqrt{1+a}$$ 之開方問題與方程式的解息息相關:若令$$x=\sqrt{1+a}$$ ,則開方求 $$x$$ 相當於求解方程式 $$x^2-(1+a)=0$$ 之實根問題。
然而,無論是傳統中算或者江戶時期的日本數學發展的過程,求解一元多項方程次時,往往利用了類似現今綜合除法的「開方法」(即賈憲-霍納法)來求方程式的數值解(相關內容與方法,可參考另一篇文章〈利用綜合除法求解多項方程式〉)。
因此,處理 $$(1+a)^{1/n}$$ 有關的展開式問題時,
便相當於求解 $$x=(1+a)^{1/n}$$,亦即求解 $$x^n-(1+a)=0$$ 的實根。
當然,若 $$1+a$$ 為實數時,我們僅需前述方法(賈憲-霍納法)便能求得其近似數值解。
然而,當 $$1+a$$ 為一般的二項「式」呢?
我們同樣可以利用綜合除法處理,但過程較複雜且冗長。
欲將 $$A$$ 開平方,可令 $$A=p^2+r$$,則 $$\sqrt A=\sqrt {{p^2} + r}= p\sqrt {1 +\frac{r}{{{p^2}}}}$$。
例如 $$A=150$$ 時,可令 $$p=12$$,此時 $$r=4$$。
通常 $$r$$ 比 $$p^2$$ 小很多,於是 $$\frac{r}{p^2}$$ 也比 $$1$$ 小很多。
因此求 $$\sqrt{A}$$ 或 $$\sqrt{p^2+r}$$ 問題都可以化成 $$(1+a)^{\frac{1}{2}}$$ 類問題。
以下筆者僅以 $$(1+a)^{\frac{1}{2}}$$ 的情況為例,說明如何利用綜合除法逐次開方,將此二項式展開。
如前述,欲求 $$(1+a)^{\frac{1}{2}}$$,即求 $$x^2-(1+a)=0$$ 之實根。
由於 $$a<1$$,我們先取 $$1$$ 作為第一個近似根,接著重複利用綜合除法:
可將原方程式 $$x^2-(1+a)=0$$ 化成 $$(x-1)^2+2(x-1)-a=0$$。
接著,令 $$x_1=x-1$$ 可得新方程式 $$x_1^2+2x_1-a=0$$。
接著,再利用綜合除法來估計 $$x_1^2+2x_1-a=0$$ 的近似根。
由於原式中帶有未知數 $$a$$,我們無法直接估計其根,
因此先令其近似根為 $$k$$,利用綜合除法:
觀察發現我們所欲取的 $$k$$,需能消去餘式中的 $$a$$,再加上 $$k^2$$ 很小可先忽略,
因此取 $$k$$ 滿足 $$-a+2k=0$$,即 $$k=\frac{a}{2}$$。
如此,可取 $$\frac{a}{2}$$ 作為 $$x_1^2+2x_1-a=0$$ 的近似根,再重複利用綜合除法:
可將 $$x_1^2+2x_1-a=0$$
化為 $${({x_1} – \frac{a}{2})^2} + (2 + a)({x_1} – \frac{a}{2}) + {(\frac{a}{2})^2} = 0$$,
再令 $$x_2=x_1-\frac{a}{2}$$,可得新方程式 $${x_2}^2 + (2 + a){x_2} + {(\frac{a}{2})^2} = 0$$。
接著,再利用綜合除法來估計 $${x_2}^2 + (2 + a){x_2} + {(\frac{a}{2})^2} = 0$$ 的近似根。
由於原式中同樣帶有未知數 $$a$$,我們無法直接估計其根,因此先令其近似根為 $$k$$,利用綜合除法:
假設 $$ak$$ 與 $$k^2$$ 很小,易知我們所欲取的 $$k$$,需能消去餘式中的 $$(\frac{a}{2})^2$$,
故令 $$(\frac{a}{2})^2+2k=0$$,可得 $$k=-\frac{a^2}{8}$$。
如此,可取 $$k=-\frac{a^2}{8}$$ 作為 $${x_2}^2 + (2 + a){x_2} + {(\frac{a}{2})^2} = 0$$ 的近似根,再重複利用綜合除法:
可將 $${x_2}^2 + (2 + a){x_2} + {(\frac{a}{2})^2} = 0$$
化為 $${({x_2} + \frac{{{a^2}}}{8})^2} + (2 + a – \frac{{{a^2}}}{4})({x_2} + \frac{{{a^2}}}{8}) – \frac{{{a^3}}}{8} + \frac{{{a^4}}}{{64}} = 0$$,
再令 $${x_3} = {x_2} + \frac{{{a^2}}}{8}$$,可得新方程式 $${x_3}^2 + (2 + a – \frac{{{a^2}}}{4}){x_3} – \frac{{{a^3}}}{8} + \frac{{{a^4}}}{{64}} = 0$$。
以此類推,不斷利用綜合除法估算新的根,以及進行「減根變換」,得新方程式。
可繼續找出 $${x_4},{x_5},\ldots ,{x_n},\ldots$$。又由於 $${x_3} = {x_2} + \frac{{{a^2}}}{8}$$,$${x_2} = {x_1} – \frac{a}{2}$$,$$x_1=x-1$$,
可知 $$x = 1 + {x_1} = 1 + \frac{a}{2} + {x_2} = 1 + \frac{a}{2} – \frac{{{a^2}}}{8} + {x_3} =\ldots$$ ,
如此可得 $${x^2} – (1 + a) = 0$$ 的近似根,亦即求得 $${(1 + a)^{\frac{1}{2}}}$$ 的展開式:
$${(1 + a)^{\frac{1}{2}}} = 1 + \frac{a}{2} – \frac{{{a^2}}}{8} + \frac{{3{a^3}}}{{48}} -\ldots$$
此即為二項式展開式的推廣至指數為 $$1/2$$ 的結果。同時,亦可推得下述結果:
$${({a^2} + r)^{\frac{1}{2}}} = a + \frac{r}{{2a}} – \frac{{{r^2}}}{{8{a^2}}} + \frac{{3{r^3}}}{{48{a^3}}} -\ldots$$
依此方法,江戶時期日本數學家(簡稱和算家)便可求解 $$x^n-(1+a)=0$$ 之實根,亦相當於處理了 $$(1+a)^{1/n}$$ 相關的展開式問題。至於其它有理冪次的推廣,請參見〈二項式定理的推廣(三):和算家的數學表〉一文。



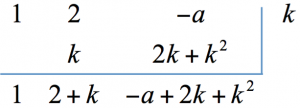
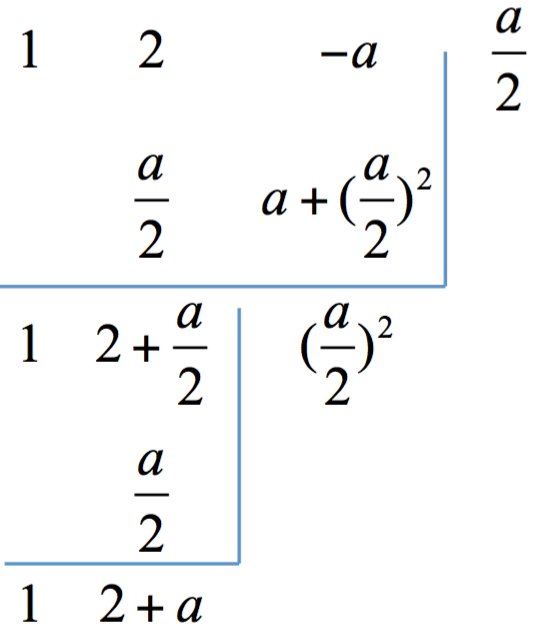
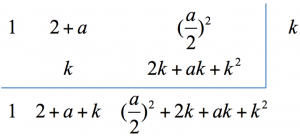
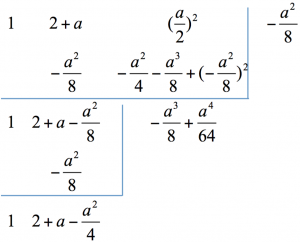
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題 
