空間向量的外積及幾何意義

空間向量的外積及幾何意義 ( The cross product and its geometric interpretation )
臺北市立和平高中黃俊瑋教師

現今高二下有關空間向量的教材提到，若 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 為空間中的兩向量，則定義 \(\overrightarrow a\) 與 \(\overrightarrow b\) 兩向量之外積

\(\overrightarrow a\times \overrightarrow b=(\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|)\)。

另一方面，空間中 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 兩向量所張成的平行四邊形面積為：

\(A = \sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}}\)

眼尖的讀者，不難發現  \(\overrightarrow a\times\overrightarrow b\) 之長恰為此平行四邊形之面積值，即 \(A = \left| {\overrightarrow a\times\overrightarrow b }\right|\)。

在現今高中課綱之下，若干版本的教科書是先定義向量的外積後，將此關係列為一性質。另有版本的教科書則是據此關係來定義空間中兩向量的外積，該教科書中先利用兩向量所張成平行四邊形的面積公式：

\(A = \sqrt {{{\left| {\overrightarrow a } \right|}^2}{{\left| {\overrightarrow b } \right|}^2} – {{(\overrightarrow a \cdot\overrightarrow b )}^2}}\)

將坐標向量 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 代入後即得：

\(A = \sqrt {({a_1}^2 + {a_2}^2 + {a_3}^2)({b_1}^2 + {b_2}^2 + {b_3}^2) – {{({a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3})}^2}}\)

整理後可推得 \(A = \sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}}\)。

接著，將向量 \((\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|)\)
定為 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 的外積。

如此可看出，\(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 其外積的長度
為 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 兩向量所張成的平行四邊形面積。

就此定義或性質來看，兩向量外積之長恰等於其所張成的平行四邊形面積，這樣的關係非常巧妙：

\(\left| {\overrightarrow a \times \overrightarrow b } \right| = \sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}}\)

這也不免令人好奇，是巧合嗎？亦或者背後有什麼樣的關連或幾何上的意義呢？以下我們簡單說明。

與外積 \(x\) 分量有關的行列式值 \(A_1=|\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right||\) 來看，其幾何意義如下：

由 \((a_1,a_2)\) 與 \((b_1,b_2)\) 兩平面向量所張成之平行四邊形面積為 \(A_1\)

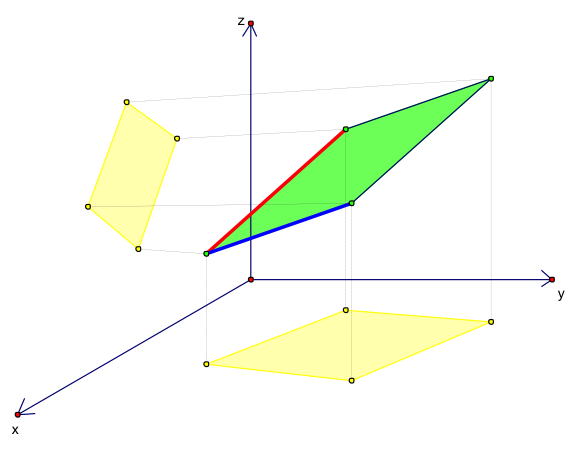
若我們將 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 兩向量所張成的平行四邊形投影到三個坐標平面後會發現，當投影到 \(xy\) 平面時，即為 \(\overrightarrow a_{xy}= ({a_1},{a_2},0)\) 與 \(\overrightarrow b_{xy}= ({b_1},{b_2},0)\) 所張成之平行四邊形，若不考慮 \(z\) 分量，則由 \((a_1,a_2)\) 與 \((b_1,b_2)\) 兩向量所張成之平行四邊形面積為 \(A_1=|\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right||\)。同理，投影到 \(yz\) 平面時，所得平行四邊形的面積為 \(A_2=|\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right||\) ；投影到 \(xz\) 平面時，所得平行四邊形的面積為 \(A_3=|\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right||\)。

如圖一所示，此圖為空間中兩向量張成之平行四邊形（綠色）在 \(xy\) 平面與 \(xz\) 平面上的投影（黃色）示意圖。

圖一 空間中兩向量張成之平行四邊形在 \(xy\) 平面與 \(xz\) 平面上的投影示意圖

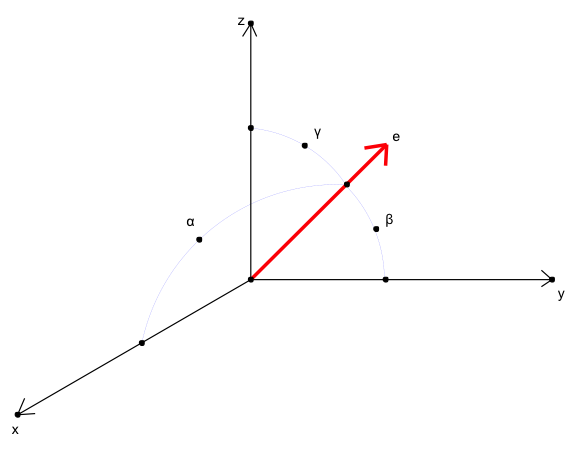
設向量 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 所在平面 \(E\) 與 \(xy\) 平面之夾角為 \(\alpha\)
（即平面的傾斜角），由於 \(\overrightarrow a= ({a_1},{a_2},{a_3})\)、\(\overrightarrow b= ({b_1},{b_2},{b_3})\) 之外積 \((\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|)\) 可作為平面 \(E\) 之法向量，而 \(z\) 軸正向上的單位向量 \((0,0,1)\) 為 \(xy\) 平面之法向量，因此可得：

 \(\left| {\cos \alpha } \right| = \frac{{|\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right||}}{{\sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}} }} = \frac{{{A_1}}}{A}\)

同理，設平面 \(E\) 與 \(yz\) 平面之夾角為 \(\beta\)，利用 \(\overrightarrow a\times\overrightarrow b\) 與 \(yz\) 平面之法向量 \((1,0,0)\) 可得：

\(|\cos \beta | = \frac{{|\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right||}}{{\sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}} }} = \frac{{{A_2}}}{A}\)

最後，設平面 \(E\) 與 \(xz\) 平面之夾角為 \(\gamma\)，可得：

 \(|\cos \gamma | = \frac{{|\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right||}}{{\sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}} }} = \frac{{{A_3}}}{A}\)

上述關係說明了 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\) 兩向量所張成平行四邊形，在 \(xy\) 平面、\(yz\) 平面與 \(xz\) 平面上的投影面積 \(A_1,A_2,A_3\) 與原面積 \(A\) 之間滿足：

\(A|\cos\alpha|=A_1,A|\cos\beta|=A_2,A|\cos\gamma|=A_3\)。

另一方面，若空間中任一向量 \(\overrightarrow e=(x,y,z)\) 與三坐標軸方向 \((0,0,1)\)、\((0,1,0)\)、\((1,0,0)\) 之夾角分別為 \(\alpha\)、\(\beta\) 與 \(\gamma\)，則其餘弦值 \(\cos\alpha\)、\(\cos\beta\) 與 \(\cos\gamma\) 稱為該向量之方向餘弦，
由於 \(\cos \alpha= \frac{z}{{\sqrt {{x^2} + {y^2} + {z^2}} }}\)、\(\cos \beta= \frac{y}{{\sqrt {{x^2} + {y^2} + {z^2}} }}\)、\(\cos \gamma= \frac{x}{{\sqrt {{x^2} + {y^2} + {z^2}} }}\)，
易知 \({\cos ^2}\alpha+ {\cos ^2}\beta+ {\cos ^2}\gamma= 1\)。

圖二 空間中向量 \(\overrightarrow e\) 與三坐標軸夾角 \(\alpha\)、\(\beta\)、\(\gamma\) 之示意圖

又上述平面 \(E\) 與三坐標平面夾角的餘弦值 \(\cos\alpha\)、\(\cos\beta\) 與 \(\cos\gamma\) 分別為 \(\overrightarrow a\times\overrightarrow b\) 的方向餘弦，因此，\({\cos ^2}\alpha+ {\cos ^2}\beta+ {\cos ^2}\gamma= 1\)，亦即 \({\left( {\frac{{{A_1}}}{A}} \right)^2} + {\left( {\frac{{{A_2}}}{A}} \right)^2} + {\left( {\frac{{{A_3}}}{A}} \right)^2} = 1\)，如此可得下式：\(\sqrt {{A_1}^2 + {A_2}^2 + {A_3}^2}= A\)。

由此關係式即可看出
空間中兩向量 \(\overrightarrow a\) 與 \(\overrightarrow b\) 其外積之長 \(\sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}}\)
恰等於 \(\overrightarrow a\) 與 \(\overrightarrow b\) 之外積所張成的平行四邊形面積。

換句話說，\(\overrightarrow a\times \overrightarrow b\) 的 \(x\)、\(y\) 與 \)z\) 分量 \(\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|\)、\(\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|\)、\(\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|\) 與 \(\overrightarrow a\) 和 \(\overrightarrow b\) 所張成之平行四邊形在三坐標平面上的投影面積 \(A_1,A_2,A_3\) 有關。

利用方向餘弦可將這三個投影面積 \(A_1,A_2,A_3\) 與 \(\overrightarrow a\) 和 \(\overrightarrow b\) 所張成之平行四邊形面積 \(A\) 作連結：

\(\sqrt {{A_1}^2 + {A_2}^2 + {A_3}^2}= A\)

而此式即說明了下述關係與幾何意義：

空間中兩非零向量 \(\overrightarrow a= ({a_1},{a_2},{a_3})\) 與 \(\overrightarrow b= ({b_1},{b_2},{b_3})\)，
其外積之長 \(\left| {\overrightarrow a\times \overrightarrow b } \right|\) 恰等於\(\overrightarrow a\) 與 \(\overrightarrow b\)兩向量所張成的平行四邊形面積

\(A = \sqrt {{{\left| {\begin{array}{*{20}{c}} {{a_2}}&{{a_3}}\\ {{b_2}}&{{b_3}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_3}}&{{a_1}}\\ {{b_3}}&{{b_1}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}\\ {{b_1}}&{{b_2}} \end{array}} \right|}^2}} \)。