重複組合（一）：相關課程之統整與反思

重複組合（一）：相關課程之統整與反思
Combination with repetition (I)：Integration and reflection of related curriculum
臺北市立和平高中教師黃俊瑋

現今課程綱要的排列組合單元裡，重複組合是較困難的概念。特別是多次利用一一對應原理，將求原問題的組合數，轉換成求方程式的非負整數解個數，最後再轉換成組合公式計算出其數。雖然可得公式，但此組合公式與原情境的直觀連結不易。因此，本文的第一部份，先簡單回顧統整重複組合相關概念與問題。第二部份，則對重複組合的公式提出另一直觀的解釋。

首先，從甲、乙、丙、丁、戊共 \(5\) 件相異物（或 \(5\) 個人）中任選三物（或 \(3\) 個人），這是一般的組合問題，其方法數為 \(C_3^5\)。其中的每物或每人選可被選中一次，例如：「甲乙丙」、「甲乙丁」與「乙丙丁」等皆為可能的情況。而所謂的重複組合問題，即是每物或每人皆可重複地被選取，換句話說，可能選出的人選為「甲甲乙」或者「丁丁丁」等情況，當然也包含了上述「甲乙丙」、「甲乙丁」與「乙丙丁」等三種情況。不難看出，放寬到可重複選取的情況時，可能的組合數明顯變多了。而一般組合與重複組合最大的差異，在於被選的對象是否可重複地被選取。

因此，我們該如何發揮排列組合的精神，以有系統的方式進行計數呢？以下我們舉一實際例子作說明。假設今天體育課，老師要求體育股長從籃球、排球與足球這 \(3\) 類球當中，共借 \(5\) 個球，每類球的個數均多於 \(5\) 個，那麼，共有多少種可能的借法呢？

這個問題的情境，即是在 \(3\) 類物品中（每類物個數多於 \(5\) 個），可重複地選出 \(5\) 個來，亦是標準的重複組合情境。不過，對初學者而言，恐怕只能掐指一算，認真地「數一數」；或以樹狀圖或討論的方式，較有系統地窮舉出所有可能性。
當然，假設籃球借 \(x\) 個、排球借 \(y\) 個而足球借 \(z\) 個，
那麼此問題馬上可轉化成為 \(x+y+z=5\) 之非負整數解個數問題。
這主要是因為每一種借法皆與方程式的一組非負整數解一一對應，例如：「籃球 \(2\) 個、排球 \(2\) 個、足球 \(1\) 個」\(\leftrightarrow(2,2,1)\)；「籃球 \(1\) 個、排球 \(0\) 個、足球 \(4\) 個」\(\leftrightarrow(1,0,4)\) 等因此，由一一對應原理可知「借法數」與「重複組合數」與「非負整數解個數」相等。

然而，處理此方程式的非負整數解個數問題的方法，同樣不脫窮舉出所有可能的解。至此，整個問題未有進展。於是課本進一步提出的處理方法為：

將五個球○○○○○與2個分隔記號｜｜作排列

如此一來，一種排法可對應到一組解。例如：「○○｜○○｜○」\(\leftrightarrow(2,2,1)\)；「○｜｜○○○○」\(\leftrightarrow(1,0,4)\)，因此，依據一一對應原理，「排列數」即與原問題的「借法數」相等。

這裡需注意的是，欲將 \(5\) 個球分隔成 \(3\) 區，需要 \((3-1)=2\) 個分隔記號。
利用「有相同物的直線排列」可知，其排法數為 \(\frac{{7!}}{{5!2!}} = \frac{{(5 + 3 – 1)!}}{{5!(3 – 1)!}}\)，
而此排列數又等於 \(C_3^{5+(3-1)}\)，
因此，從 \(3\) 類物（每類物超過 \(5\) 個）可重複地選出 \(5\) 物的組合數，
等於方程式 \(x+y+z=5\) 的非負整數解個數，等於 \(\frac{{(5 + 3 – 1)!}}{{5!(3 – 1)!}} = C_3^{5 + (3 – 1)}\)。
如此便解決了此問題。

而上述例子與討論過程，可作一般化：

從 \(n\) 類物（每類物超過 \(k\) 個）可重複地選出 \(k\) 個的組合數，
等於方程式 \(x_1+x_2+\cdots+x_n=k\) 的非負整數解個數，
亦等於 \(\frac{{(k + n – 1)!}}{{k!(n – 1)!}} = C_k^{k + n – 1}\)。

以下再舉一相關例子：\(5\) 個相同物，分給 \(3\) 個人，每人可兼得（即可全拿或不拿），共有多少種分法呢？因為問題中的各物相同，我們只需考慮每個人所拿個數。因此，可假設第一個人分到 \(x\) 個、第二個人分到 \(y\) 個，而第三個人分到 \(z\) 個。由於 \(3\) 人共拿 \(5\) 個，因此本問題亦可化成方程式 \(x+y+z=5\) 求非負整數解個數問題。

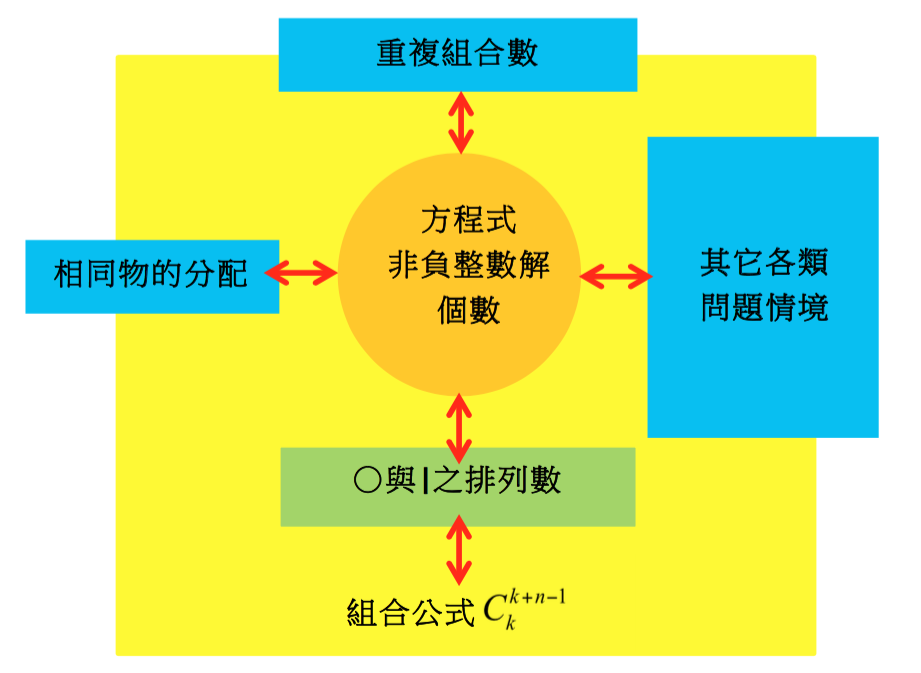
由此來看，一般的相同物分配問題，事實上皆可化約為 \(x_1+x_2+\cdots+x_n=k\) 類方程式求非負整數解個數問題。所以，重複組合、非負整數解以及相同物的分配等三類問題背後，都具有共通的數學模型。除此之外，尚有許多問題情境，其解問題的過程皆可化約成多元一次方程式求非負整數解問題，因而，可以利用相同的組合公式求解。我們可將重複組合相關課程內容，整理得圖一之關係圖：

圖一 重複組合相關問題與理論關係圖

其中，方程式求非負整數解扮演了核心角色。無論問題情境如何變化，只要能從相關問題的情境中，提煉出「\(x_1+x_2+\cdots+x_n=k\)」類的方程式（數學模型），並且問題的方法數等於該方程式之非負整數解個數，那麼，皆可同於上述操作方式求解，得方法數為 \(C_k^{k + n – 1}\)。

綜合來看，高中數學重複組合相關教材，反應出多題一解的特色。我們可從各類具體但相異的脈絡與情境中，抽象出隱藏在背後的共同數學模型：「多元一次方程式的非負整數解」，並可以同一方法（或公式）求解。如此一來，重複組合問題與相關公式的學習，並非孤立無用的問題與公式，而是統合了各類與多元一次方程式求非負整數解相關的問題情境。學習的過程中，不應只是死記公式，而應強調「重複組合問題本身」→「非負整數解」→「○與|的排列數」→「組合公式 \(C_k^{k + n – 1}\)」等四者間的連結與一一對應關係，待相同物的分配等新情境的加入後，可利用「方程式求非負整數解」作為主要拱心石，逐步與各類問題與情境連結。

連結：重複組合（二）：公式的一個直觀解釋