平面上點到直線距離（二）

平面上點到直線距離（二） (The distance from a point to a line in the plane Ⅱ）
臺北市立和平高中教師黃俊瑋

連結：平面上點到直線距離（一）

本文承〈平面上點到直線距離（一）〉，繼續提出三類平面上點到直線距離的解法以及相關討論與知識間的連結。

方法2：利用向量平行與垂直等關係

方法2-1：利用向量 \(PQ\) 與 \(L\) 之方向向量垂直。

利用直線 \(L:3x+4y=10\) 的參數式，
可假設 \(P(3,-6)\) 在 \(L\) 上的投影點 \(Q(2+4t,1-3t)\)，
因為 \(\overline{PQ}\) 垂直直線 \(L\)，所以 \(\overline{PQ}\) 為最短距離。
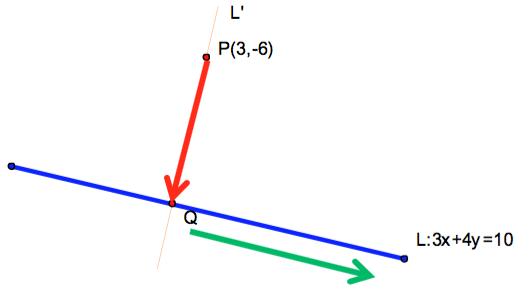
則向量 \(\vec{PQ}=(1-4t,-7+3t)\) 與 \(L:3x+4y=10\) 之方向向量 \(\vec{n}=(4,-3)\) 垂直。（如圖一所示）
因此，內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\)，解之可得 \(t = 1\)，可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

評析：這個方法所需先備知識為《第三冊》第3章－直線的方向向量、直線參數式與內積。求距離過程中，亦順便可求出投影點。此方法可推廣至空間中求點到直線距離、投影點問題，亦可用於求空間中兩平行直線距離。

圖一 向量\(\vec{PQ}\)與直線方向向量垂直

方法2-2：利用向量 \(PQ\) 與 \(L\) 之法向量平行。

利用直線 \(L:3x+4y=10\) 的參數式，
可假設 \(P(3,-6)\) 在 \(L\) 上的投影點 \(Q(2+4t,1-3t)\)，
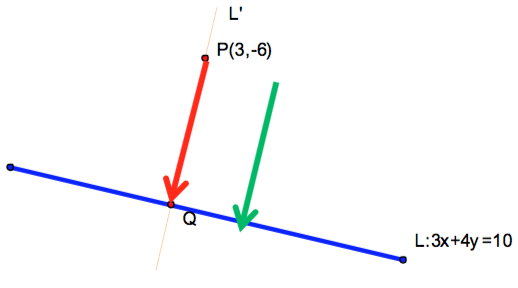
則向量 \(\vec{PQ}=(1-4t,-7+3t)\) 與 \(L:3x+4y=10\) 之法向量 \(\vec{n}=(3,4)\) 平行，（如圖二所示）
利用分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\) 之關係，可得 \(4(1-4 t) = 3 (-7+3t)\)，
解之可得 \(t = 1\)，可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

評析：這個方法所需先備知識同樣為《第三冊》第3章－直線的法向量與直線參數式。求距離過程中，亦順便可求出投影點。此法與2-1之差別主要在於利用直線的方向向量與直線的法向量。

圖一 向量\(\vec{PQ}\)與直線方向向量平行

方法3：求 \(P\) 點到直線上動點距離之最小值。

方法3-1：利用配方法求 \(P\) 點到直線上動點距離之最小值。

利用直線 \(L:3x+4y=10\) 的參數式，可假設 \(L\) 上任一動點 \(Q(2 + 4t,1 – 3t)\)
則 \(P(3,-6)\) 與 \(Q(2 + 4t,1 – 3t)\) 之距離為：
\(\sqrt {{{(2 + 4t – 3)}^2} + {{(1 – 3t + 6)}^2}}=\sqrt {25{t^2} – 50t + 50}\le\sqrt {25{{{\rm{(}}t – {\rm{1)}}}^{\rm{2}}} + {\rm{2}}5}\le\sqrt {25}{\rm{=5}}\)
即當 \(t = 1\) 時，有最短距離 \(5\)，此時 \(t = 1\) 所得之點 \(Q(6,-2)\)，
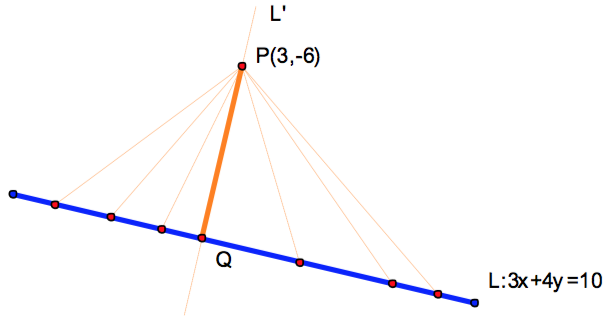
即為 \(P(3,-6)\) 在直線 \(L:3x+4y=10\) 的投影點。（如圖三所示）

評析：這個方法所需先備知識為《第一冊》第二章－二次函數配方法求極值、《第三冊》第3章－直線參數式，以及平面上的兩點距離公式。求距離過程中，亦可順便求出投影點。此方法可推廣至空間中，求點到直線距離問題。

圖三P點到直線上動點Q距離之最小值即為所求最短距離

方法3-2：利用柯西不等式求 \(P\) 點到直線上動點距離之最小值。

設 \(Q(x,y)\) 為直線 \(L:3x+4y=10\) 上任一點，
則 \(P(3,-6)\) 與 \(Q(x,y)\) 之距離平方為 \(\overline {PQ}= {(x – 3)^2} + {(y + 6)^2}\)，
利用柯西不等式 \({(3x – 9 + 4y + 24)^2} \le [{(x – 3)^2} + {(y + 6)^2}({3^2} + {4^2})\)，
可得 \({25^2} \le {\overline {PQ} ^2} \cdot 25\)，即 \({\overline {PQ} ^2}\) 的最小值為 \(25\)，\(\overline{PQ}\) 的最小值為 \(5\)。
且知，當 \(\frac{{x – 3}}{{y + 6}} = \frac{3}{4}\) 時，產生最小值，解之得 \((x,y)=(6,-2)\) ，
即為 \(P(3,-6)\) 在直線 \(L:3x+4y=10\) 的投影點。（如圖三所示）

評析：這個方法所需先備知識為《第三冊》第3章－柯西不等式。求距離過程中，亦可順便求出投影點。此方法可推廣至空間中，求點到平面距離問題。

方法4：在直線上任取一點，再利用正射影。

方法4-1：利用在法向量上的正射影長

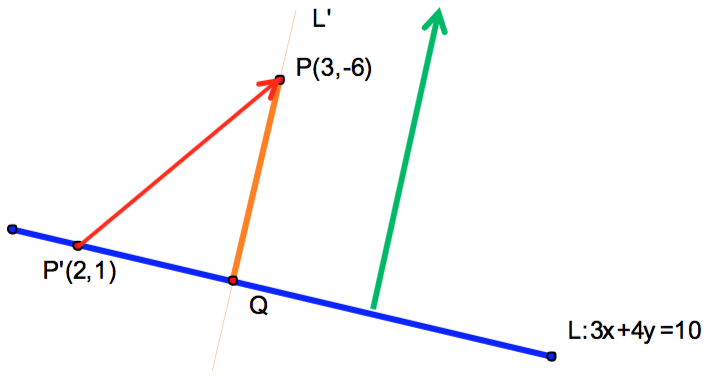
在直線 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，可得向量 \(\vec{P’P}=(1,-7)\)，
\(\vec{P’P}=(1,-7)\) 在直線法向量 \(\vec{n}=(3,4)\) 上的正射影長即為所求。（如圖四所示）
依正射影公式可得正射影為 \(\frac{{(1, – 7) \cdot (3,4)}}{{25}}(3,4) = ( – 3, – 4)\)
則正射影長為 \(5\)，即為所求點 \(P(3,-6)\) 到直線 \(L\) 的距離。

評析：這個方法所需先備知識為《第三冊》第3章－直線法向量、正射影公式。可推廣至空間中，求點到平面距離問題。

圖四 引入一點，利用在法向量上的正射影

方法4-2：利用在方向向量上的正射影長

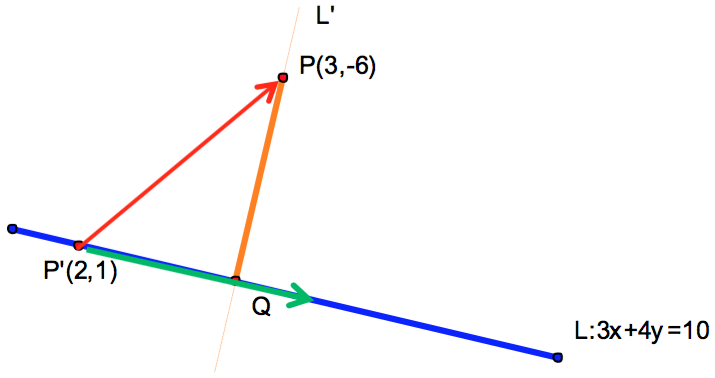
在直線 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，可得向量 \(\vec{P’P}=(1,-7)\)，
在直線方向向量 \(\vec{L}=(4,-3)\) 上的正射影長為：\(\vec{P’Q}=\frac{{(1, – 7) \cdot (4, – 3)}}{{25}}(4, – 3) = (4, – 3)\)
利用勾股定理 \({\overline {PP’}^2}= {\overline {P’Q} ^2} + {\overline {PQ} ^2}\)，可求得點 \(P(3,-6)\) 到直線 \(L\) 的距離為\(5\)。
（如圖五所示）

評析：這個方法所需先備知識為《第三冊》第3章－直線方向向量、正射影公式以及國中學過的勾股定理。不過，方法4-2顯然較為簡捷。

圖五 引入一點，利用在方向向量上的正射影

以上為三類平面上點到直線距離的解法，接下來的〈平面上點到直線距離(三)〉繼續討論另外三類解法，以及相關知識間的連結。

連結：平面上點到直線距離（三）