集合的元素個數:無窮集合(一) The cardinality of a set: Infinite sets I
集合的元素個數:無窮集合(一) The cardinality of a set: Infinite sets I
臺北市立和平高中教師黃俊瑋
無窮集合元素個數相等的定義如下:
若兩個集合(無窮集合)之間存在一一對應關係,則這兩個集合的元素個數相等。
我們可藉此發現許多違反直覺的例子。首先,就直觀上來看,正整數的個數比正偶數的個數來得多,而正整數的個數也比完全平方數來得多,不過,我們依上述定義實際作對應與比較後,會發現:
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\2&4&6&8&10&\cdots&2n\end{array}\)
換言之,正整數的個數與正偶數的個數一樣多。類似地,我們也會發現:
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\1^2&2^2&3^2&4^2&5^2&\cdots&n^2\end{array}\)
因此,正整數的個數與平方數的個數一樣多。這是不是既違反直覺又不可思議呢?
而上述自然數與其真子集之間存在一一對應關係的這個性質,正是無窮集合最重要的特色。於是乎數學家用這個性質來定義無窮集合:
集合 \(S\) 為無窮集合,若且唯若存在一個真子集 \(A\),使其元素之間可一一對應,即個數相等,
亦即 \(n(S)=n(A)\)。
換言之,前述所有自然數構成的集合,存在一個真子集(無論是正偶數構成的集合或平方數所構成的集合),使其元素個數相等,因此自然數構成的集合的確為一個無窮集合。這樣的特性與有限集合大不相同。歐里基得的《幾何原本》中,提到了「全體大於部份」這個共有概念(common notion),或稱公理。然而,這個公理僅在有限世界裡成立,上述談到的正整數、偶數與平方數等無窮集合之間,便不滿足於此公理。因此,「全體的數量可等於部份」的這個定義,正是劃分了有限集合與無窮集合之間的最大差異。
接著,我們繼續比較正整數與整數的元素個數。同樣地,直覺上,整數包含了正整數、零與負整數,想必其個數比正整數多吧!然而,我們可以在所有的整數與正整數之間,造出一一對應的關係:
\(\begin{array}{cccccccccc} 1&2&3&4&5&6&7&\cdots&2n&2n+1\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow&\updownarrow\\0&1&-1&2&-2&3&-3&\cdots&n&-n\end{array}\)
因此,所有整數所構成的集合,其元素個數還是與正整數一樣多。一般而言,我們也可以造一個從自然數送到整數,且滿足一一對應的函數:
如此,亦可看出兩個集合的元素個數一樣多。
數學上,一般我們會把元素個數和自然數一樣多的集合,稱為可數集(countable set),也就是說,一個集合,其元素可與自然數作一一對應,那麼該集合便為可數集。為了方便之後的討論,我們介紹一個定理:
定理:每個可數集的無窮子集皆可數。
證明:
令 \(S\) 為一可數集,而 \(E\) 為其無窮子集,即 \(E\subset S\)。因為 \(S\) 可數,於是我們將集合 \(S\) 裡面的不同元素作排序,形成數列 \((s_n)\),接著,我們以如下方法建構一個新的數列 \((n_k)\):
令 \(n_1\) 是滿足 \(s_{n_1}\in E\) 的最小正整數,
\(n_k\) 是滿足 \(s_{n_k}\in E\),且大於 \(n_{k-1}\) 的最小正整數,其中 \(k=2,3,4\cdots\)
令 \(a_k=s_{n_k}\),\(k=1,2,3,\cdots\),如此,我們可對集合 \(E\) 的元素作排序,並獲得了正整數 \(k\) 與 \(n_k\) 之間的一一對應關係。於是,證明了此定理。
換句話說,上述過程即是從數列 \((s_n)\) 的第一項開始檢查,第 \(1\) 個出現在子集 \(E\) 的元素令為 \(a_1\);第 \(2\) 個出現在子集 \(E\) 的元素令為 \(a_2\);以此類推,可將集合裡的元素排序,使其元素與自然數之間存在一一對應的關係。因此,我們知每個可數集的無窮子集皆可數。
接下來,回到原先的問題,那所有有理數所構成的集合呢?由於每個自然數皆可表示成有理數,例如 \(2=\frac{2}{1}\)、\(3=\frac{3}{1}=\frac{6}{2}\) 等等。但我們可以找到許許多多不是自然數的有理數,因此直觀上來看,有理數的數量應當比自然數來得多。不過,很快地你將會發現,無窮集合的世界是如此地不可思議,令人無法置信。以下我們採取所謂的「對角線」法來作點數:
圖一所示的對角線法,相當於從分子分母和為 \(2\) 的有理數開始數,順序則依分子由小排到大,接著,是分子分母和為 \(3\) 的有理數,同樣依分子由小排到大,再接著,是分子分母和為 \(4\) 的有理數,以此類推。如此我們可以將有理數作排序:
\(\displaystyle\frac{1}{1},\frac{1}{2},\frac{2}{1},\frac{1}{3},\frac{2}{2},\frac{3}{1},\frac{1}{4},\frac{2}{3},\frac{3}{2},\frac{4}{1}\cdots\)
我們把上述這些數字所構成的集合稱為 \(S\),由此排序可知,此集合為可數集。眼尖的讀者會發現,\(\frac{1}{1}\) 與 \(\frac{2}{2}\) 與 \(\frac{3}{3}\) 等有理數皆為 \(1\),因此,我們把重複的數字刪去後,可得一個 \(S\) 的無窮子集,它便是所有的有理數所形成的集合。又因為每個可數集的無窮子集亦為可數集,因此,有理數可與自然數一一對應,亦即有理數的個數與自然數一樣多。
討論至此,讀者也許會懷疑,難道所有的無窮集合之間,都存在一一對應的關係?換言之,所有無窮集合的元素個數皆相等嗎?事實並非如此,當我們將討論的對象,擴展到所有的實數時,即會發現,一切別有洞天,敬待下回分曉。


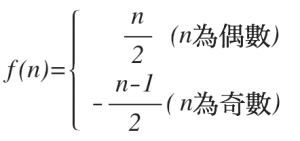

 前一篇文章
前一篇文章 下一篇文章
下一篇文章 惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2)) 
