從二項式定理到多項式定理 (2)
從二項式定理到多項式定理 (2)(From Binomial Theorem to Multinomial Theorem (2))
臺北市立第一女子高級中學蘇俊鴻老師
在〈從二項式定理到多項式定理(1)〉中提到 \((x+y)^3\) 的 \(x^2y^1\) 項是如何產生呢?由於 \({\left( {x + y} \right)^3} = \left( {x + y} \right)\left( {x + y} \right)\left( {x + y} \right)\),故可看成在三個 \((x+y)\) 括號中,二個選 \(x\) 一個選 \(y\) 相乘而得,如此選取的方法數為 \(C_1^3\),所以 \(x^2y^1\) 項的係數是 \(C_1^3=3\)。
不過,也可換個方式來看 \(x^2y^1\) 項的產生。如圖一所示,選取二個選 \(x\)、一個 \(y\) 後,其情形等同於 \(2\) 個 \(x\) 與 \(1\) 個 \(y\) 的不盡相異物直線排列。因此,\(2\) 個 \(x\)、\(1\) 個 \(y\) 的直線排列可產生 \(x^2y^1\) 項,這樣的排列方法數為 \(\frac{3!}{1!2!}=3=C_1^3\),故 \(x^2y^1\) 項的係數是 \(C_1^3=3\)。
進一步,「不盡相異物直線排列」的看法讓我們可以將 \((x+y)^n\) 推廣到形如 \({({x_1} + {x_2} +\cdots+ {x_m})^n}\) 的多項式定理(Multinomial Theorem)。
還是由 \((x+y+z)^3\) 說起,同樣的,\((x+y+z)^3\) 是 \((x+y+z)\) 連乘三次,即 \((x+y+z)(x+y+z)(x+y+z)\),易知\((x+y+z)^3\) 的展開式會有
\({x^3},{y^3},{z^3},{x^2}y,{x^2}z,{y^2}x,{y^2}z,{z^2}x,{z^2}y,xyz\)
共計 \(H_3^3 = C_3^5 = 10\) 種類型的齊次項。
每項仍是這三個括號中,選取不同數量的 \(x\) 或 \(y\) 或 \(z\) 相乘而得,每項的係數一樣對應到選取的方法數。如圖二所示,\(x^2y(=x^2y^1z^0)\) 項可視為三個括號中,\(2\) 個選 \(x\)、\(1\) 個選 \(y\)、\(0\) 個選 \(z\),做不盡相異物的直線排列,方法數為 \(\frac{3!}{2!1!0!}=3\)。因此,\(x^2y\) 項的係數為 \(3\)。
同理,\(xyz(=x^1y^1z^1)\) 項則是三個括號中,\(1\) 個選 \(x\)、\(1\) 個選 \(y\),\(1\) 個選 \(z\),做不盡相異物的直線排列,方法數為 \(\frac{3!}{1!1!1!}=6\),故 \(xyz\) 的係數為 \(6\)。
因此,\((x+y+z)^3\) 的展開式為
\(\begin{array}{ll} (x + y + z)^3 &= {x^3} + {y^3} + {z^3} + \frac{{3!}}{{2!1!0!}}{x^2}{y^1}{z^0} + \frac{{3!}}{{2!0!1!}}{x^2}{y^0}{z^1} + \frac{{3!}}{{1!2!0!}}{x^1}{y^2}{z^0} + \frac{{3!}}{{0!2!1!}}{x^0}{y^2}{z^1} + \frac{{3!}}{{1!0!2!}}{x^1}{y^0}{z^2} + \frac{{3!}}{{0!1!2!}}{x^0}{y^1}{z^2} + \frac{{3!}}{{1!1!1!}}{x^1}{y^1}{z^1} \\&=\sum\limits_{ a + b + c = 3 \atop 0 \le a,b,c \le 3}^{}{\frac{{3!}}{{a!b!c!}}{x^a}{y^b}{z^c}}\end{array}\)
雖然式子看來繁複些,但係數的規律與二項式定理並無二致。
只是超過二項,無法只用組合數 \(C\) 來表示。
仿照上述看法,不難類推出形如 \((x_1+x_2+\cdots+x_m)^n\) 展開式中的各項係數與其展開式,
\(({x_1} + {x_2} +\cdots+ {x_m})^n= \sum\limits_{{k_1} + {k_2} + \cdots + {k_m} = n \atop 0 \le {k_1},{k_2},\cdots,{k_m} \le n} {\frac{{n!}}{{{k_1}!{k_2}! \cdots {k_m}!}}{x_1}^{{k_1}}{x_2}^{{k_2}}\cdots{x_m}^{{k_m}}}\)
其中 \(\frac{{n!}}{{{k_1}!{k_2}! \cdots {k_m}!}}{x_1}^{{k_1}}{x_2}^{{k_2}} \cdots {x_m}^{{k_m}}\) 稱為展開式的一般項。
實際操作一遍,比較能掌握符號的意義,試試 \((x+y+z)^4\) 的展開式,
共有 \(H_4^3=C_4^6=15\) 項
\(\begin{array}{ll}{(x + y + z)^4} &= \frac{{4!}}{{4!0!0!}}{x^4}{y^0}{z^0} + \frac{{4!}}{{0!4!0!}}{x^0}{y^4}{z^0} + \frac{{4!}}{{0!0!4!}}{x^0}{y^0}{z^4} + \frac{{4!}}{{3!1!0!}}{x^3}{y^1}{z^0} + \frac{{4!}}{{3!0!1!}}{x^3}{y^0}{z^1} + \frac{{4!}}{{1!3!0!}}{x^1}{y^3}{z^0} + \frac{{4!}}{{0!3!1!}}{x^0}{y^3}{z^1} + \frac{{4!}}{{1!0!3!}}{x^1}{y^0}{z^3} + \frac{{4!}}{{0!1!3!}}{x^0}{y^1}{z^3} + \frac{{4!}}{{2!2!0!}}{x^2}{y^2}{z^0} + \frac{{4!}}{{2!0!2!}}{x^2}{y^0}{z^2}+ \frac{{4!}}{{0!2!2!}}{x^0}{y^2}{z^2} + \frac{{4!}}{{2!1!1!}}{x^2}{y^1}{z^1} + \frac{{4!}}{{1!2!1!}}{x^1}{y^2}{z^1}+\frac{{4!}}{{1!1!2!}}{x^1}{y^1}{z^2}\\&= {x^4} + {y^4} + {z^4} + 4{x^3}y + 4{x^3}z + 4x{y^3} + 4{y^3}z + 4x{z^3} + 4y{z^3} + 6{x^2}{y^2} + 6{x^2}{z^2} + 6{y^2}{z^2} + 12{x^2}yz + 12x{y^2}z + 12xy{z^2}\end{array}\)
當全部展開時,式子相當龐雜,但其規律不難掌握!相信再耐心看個幾遍應能漸入佳境。最好的測試,就是計算看看 \((x+3y-z)^6\) 展開式中 \(x^2yz^3\) 項的係數,希望你/妳能得出答案為 \(-180\)。


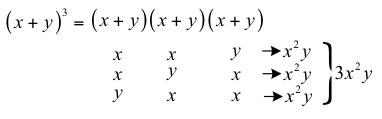
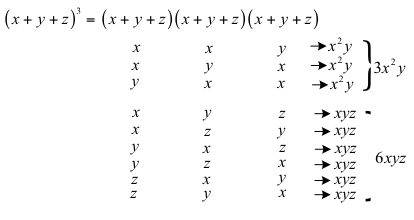
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria) 
