從二項式定理到多項式定理 (1)
從二項式定理到多項式定理 (1)(From Binomial Theorem to Multinomial Theorem (1))
臺北市立第一女子高級中學蘇俊鴻老師
國中時學到乘法公式 \({(x + y)^2} = {x^2} + 2xy + {y^2}\),\({(x + y)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\),就在猜想 \({(x + y)^4},{(x + y)^5},\cdots,{(x + y)^n}\) 展開後的模樣。透過比對可看出 \((x+y)^n\) 的各項都是齊次,也就是說,展開的各項 \(x^ay^b\) 都會滿足 \(a+b=n\)。
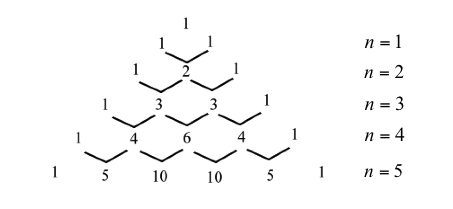
因此,只要能掌握各項係數的規則,任意的自然數 \(n\),我們便能將 \((x+y)^n\) 的各項依 \(x\) 或 \(y\) 的升冪或降冪排出。國中老師採用的方法是將巴斯卡三角形畫出(圖一),一一對應,只要足夠耐心,就能達到任意的自然數 \(n\)。
這個關於 \((x+y)^n\) 展開式每項係數的規則,就是初等代數中重要的二項式定理(Binomial Theorem)。事實上,透過排列組合的相關知識,就能推論出 \((x+y)^n\) 展開式各項的係數規則。這也為何高中數學將二項式定理當成排列組合的一個應用。
首先,從 \((x+y)^3\) 的展開過程觀察起。由於
\(\begin{array}{ll}{\left( {x + y} \right)^3} &= \left( {x + y} \right)\left( {x + y} \right)\left( {x + y} \right) \\&= xxx + xxy + xyx + yxx + xyy + yxy + yyx + yyy \\&= {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\end{array}\)
換言之,\((x+y)^3\) 是 \((x+y)\) 連乘三次,即 \((x+y)(x+y)(x+y)\)。展開得到的各項相當於在每一個括號中,各選一個 \(x\) 或 \(y\) 作乘積而得。由於乘法可以交換,進一步能整理成 \(x^3,x^2y^1,x^1y^2,y^3\) 四種類型的項,而同類項的個數就是每項的係數。
也就是說,從這三個括號中,個別選取 \(x\) 或 \(y\) 來作乘積,其方法數就是每個對應項的係數。舉例來說,如圖二所示,\(x^2y^1\) 是三個括號中,\(2\) 個選 \(x\),\(1\) 個選 \(y\),它的方法有 \(C^3_1=3\) 種,故項係數可以組合數 \(C_1^3\) 表示。
因此,我們可依選取 \(y\) 的個數之規律,寫出 \((x+y)^3\) 的展開式 (請注意式中紅字的對應關係)
仿此作法,我們能類推出 \((x+y)^n\) 的展開式,同樣請讀者注意式中紅字的對應關係:
因此,二項式定理為
對於任意正整數 \(n\),我們有下列的二項展開式:
\(\begin{array}{ll}{\left( {x + y} \right)^n} &= C{\kern 1pt} _0^n{x^n} + C_1^n{x^{n – 1}}{y^1} +\cdots+ C{\kern 1pt} _r^n{x^{n – r}}{y^r} +\cdots+ C{\kern 1pt} _{n – 1}^n{x^1}{y^{n – 1}} + C{\kern 1pt} _n^n{y^n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\\&= \sum\limits_{r = 0}^n {C{\kern 1pt} _r^n{x^{n – r}}{y^r}}\end{array}\)
其中,形如 \(C_r^nx^{n-r}y^r\) 被稱為展開式的一般項。
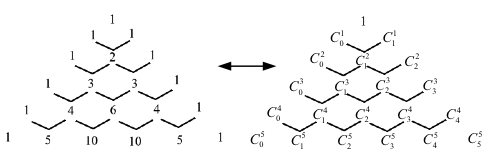
若將巴斯卡三角形重新用組合數寫上一遍(如圖三),易知巴斯卡三角形的構造規則為 \(C_m^n = C_{m – 1}^{n – 1} + C_m^{n – 1}\),\(1\le m\le n-1\)。這正是這個組合恆等式被稱為巴斯卡定理的原因。事實上,我們也能用數學歸納法和巴斯卡定理證明二項式定理,有興趣的讀者不妨嘗試看看。
有了二項式定理,對於處理高次展開幫助甚大,比方說,多項式函數 \(f(x)=(1+x)^{10}\) 的展開式
\(f(x) = {(1 + x)^{10}} = C_0^{10} + C_1^{10}x + C_2^{10}{x^2} +\cdots+ C_{10}^{10}{x^{10}}\)
也使得形如 \((1.01)^{10}\) 的估計,除了利用對數取值查表,又多了一種方法,由於
\(\begin{array}{ll}{(1.01)^{10}} &= f(0.01) \\&= C_0^{10} + C_1^{10}(0.01) + C_2^{10}{(0.01)^2} +\cdots+ C_{10}^{10}{(0.01)^{10}}\end{array}\)
取前四項即可求值準確到小數點以下第三位,
\(C_0^{10} + C_1^{10}(0.01) + C_2^{10}{(0.01)^2} + C_3^{10}{(0.01)^3} \\= 1 + 10 \times (0.01) + 45 \times {(0.01)^2} + 120 \times {(0.01)^3} \\= 1 + 0.1 + 0.0045 + 0.00012 = 1.10462 \approx 1.1046\)
不過,若是變數超過二項,該如何處理呢?例如,\((x+y+z)^3\) 的展開式,我們可以這麼做
\(\begin{array}{ll}{(x + y + z)^3} &= {[(x + y) + z]^3} \\&= C_0^3{(x + y)^3} + C_1^3{(x + y)^2}z + C_2^3(x + y){z^2} + C_3^3{z^3} \\&= C_0^3(C_0^3{x^3} + C_1^3{x^2}y + C_2^3x{y^2} + C_3^3{y^3}) + C_1^3(C_0^2{x^2} + C_1^2xy + C_2^2{y^2})z + C_2^3(x + y){z^2} + C_3^3{z^3} \\&= {x^3} + {y^3} + {z^3} + 3{x^2}y + 3{x^2}z + 3x{y^2} + 3{y^2}z + 3x{z^2} + 3y{z^2} + 6xyz\end{array}\)
從過程來看,只要反覆運用二項式定理,還是能處理二項以上的展開式。但讓人好奇的是,是否有類似二項展開的定理呢?有的,答案是多項式定理(Multinomial Theorem)。更讓人興奮的是,推論它的方法也和本文所談的二項式定理相同。有興趣的讀者不妨嘗試看看,我們將在〈從二項式定理到多項式定理(2)〉中揭曉。


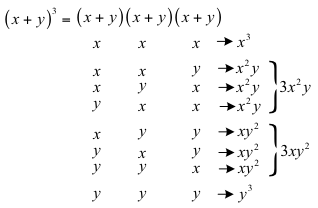
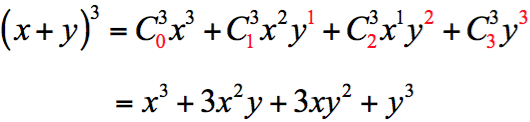
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria) 
