條件句與對偶命題 (Conditional and contrapositive statements)
條件句與對偶命題 (Conditional and contrapositive statements)
臺北市立和平高中黃俊瑋教師
在數學上,有許多敘述句皆具有下列形式:\(P\) 蘊涵 \(Q\)
而它的意義即為:若 \(P\) 為真,則 \(Q\) 也必須為真
此外,尚包含了其它與蘊涵相關的術語,例如:若 \(P\) 則 \(Q\) 、\(P\) 是 \(Q\) 的充分條件、\(P\) 唯若 \(Q\)、\(Q\) 若 \(P\) 以及 \(Q\) 是 \(P\) 的必要條件等,而這些術語的意義皆相同。例如,「若 \(n^2\) 為偶數,則 \(n\) 為偶數」、「若 \(x\) 與 \(y\) 皆為有理數,則 \(x+y\) 為有理數」以及「若 \(\Delta ABC\) 為直角三角形,則斜邊平方等於兩股之平方和」等,都是此類具蘊涵關係的敘述句。
一般而言,蘊涵關係包含了涉及真值(truth)的條件句與因果關係(causation)兩部份,我們以符號「\(P \Rightarrow Q\)」來表示 \(P\) 蘊涵 \(Q\) 的真值部份,並把具「\(P \Rightarrow Q\)」這種形式的句子,稱為條件表達式或簡稱為條件句。其中 \(P\) 的稱為前項或前件(antecedent), \(Q\) 則稱為後項或後件(consequent)。
一個條件句的真值,可利用其前項與後項的真值來定義。換句話說,條件句 \(P \Rightarrow Q\) 是否為真,完全取決於 \(P\) 與 \(Q\) 的真假值。首先,若 \(P\) 與 \(Q\) 之間存在實值的蘊涵關係,那麼 \(P\) 蘊涵了 \(Q\),因此,\(P\) 的真值蘊涵了 \(Q\) 的真值。所以,當 \(P\) 與 \(Q\) 皆為真時,\(P \Rightarrow Q\) 當然為真。
若 \(P\) 為真但 \(Q\) 為假呢?如果發生了雖然 \(P\) 為真但 \(Q\) 仍為假的情況,這意味著 \(P\) 並不蘊涵 \(Q\),即意 ![]() ,換言之,\(P \Rightarrow Q\) 為假。因此,我們將
,換言之,\(P \Rightarrow Q\) 為假。因此,我們將 ![]() 為真,定義成「\(P\) 為真但 \(Q\) 為假」。接著,又因為其否定敘述為 \(P \Rightarrow Q\),因此,當
為真,定義成「\(P\) 為真但 \(Q\) 為假」。接著,又因為其否定敘述為 \(P \Rightarrow Q\),因此,當 ![]() 假時,條件句 \(P \Rightarrow Q\) 為真。
假時,條件句 \(P \Rightarrow Q\) 為真。
如此一來,我們只要檢查 ![]() 的定義「\(P\) 為真但 \(Q\) 為假」便可知,只要滿足下列條件之一,那麼 \(P \Rightarrow Q\) 為真:
的定義「\(P\) 為真但 \(Q\) 為假」便可知,只要滿足下列條件之一,那麼 \(P \Rightarrow Q\) 為真:
- \(P\) 與 \(Q\) 皆為真
- \(P\) 為假與 \(Q\) 為真
- \(P\) 與 \(Q\) 皆為假
如此,可得表一中「\(P \Rightarrow Q\) 之邏輯真值表」。
在表二裡,我們造出 \(P \Rightarrow Q\) 與 \(\neg P \lor Q\) 之邏輯真值表,
從此表中,我們發現 \(P \Rightarrow Q\) 與 \(\neg P \lor Q\) 的邏輯真值表完全相同,
因此,\(P \Rightarrow Q\) 與 \(\neg P \lor Q\) 在邏輯上等價。
在表三裡,我們則造出 ![]() 與 \(P\land \neg Q\) 之邏輯真值表,
與 \(P\land \neg Q\) 之邏輯真值表,
從此表中,我們發現![]() 與 \(P\land \neg Q\) 的邏輯真值表完全相同,
與 \(P\land \neg Q\) 的邏輯真值表完全相同,
因此,![]() 與 \(P\land \neg Q\) 在邏輯上等價
與 \(P\land \neg Q\) 在邏輯上等價
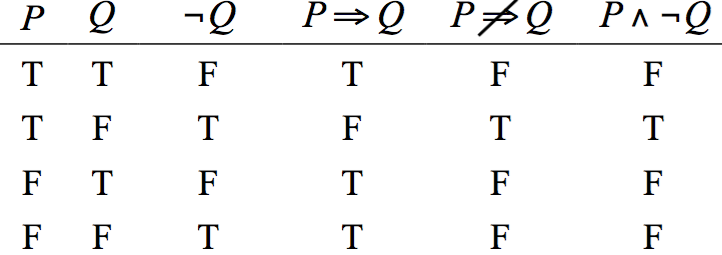
表三\(~~~\)![]() 與 \(P\land \neg Q\) 之邏輯真值表
與 \(P\land \neg Q\) 之邏輯真值表
最後,我們把 \(\neg Q \Rightarrow \neg P\) 稱為 \(P \Rightarrow Q\) 的對偶命題。
從表四來看,我們發現 \(P \Rightarrow Q\) 與 \(\neg Q \Rightarrow \neg P\) 的邏輯真值表完全相同,
因此,\(P \Rightarrow Q\) 與 \(\neg Q \Rightarrow \neg P\) 在邏輯上等價。
一般而言,一個條件句會與其對偶命題在邏輯上等價。
因此,當我們需要證明諸如 \(P \Rightarrow Q\) 之蘊涵關係時,
可透過證明其對偶命題 \(\neg Q \Rightarrow \neg P\) 的方式。
我們舉一個高中課程裡常見的例子來說明對偶命題的等價性。
設 \(n\) 為正整數,當我們想要證明敘述句「若 \(n^2\) 為偶數,則 \(n\) 為偶數」時,發現並不好下手(讀者可自行思考、嘗試),因此,可轉而證明「若 \(n\) 不為偶數,則 \(n^2\) 不為偶數」。證明如下:
因為 \(n\) 為正整數且不為偶數,所以,\(n\) 為奇數,
故可設 \(n=2k-1\),其中,\(k\) 為正整數。
則 \({n^2} = {(2k – 1)^2} = 4{k^2} + 4k + 1 = 2(2{k^2} + 2k) + 1\) 必為奇數,
故 \(n^2\) 不為偶數。
如此,證明了「若 \(n\) 不為偶數,則 \(n^2\) 不為偶數」為真,
亦相當於證明了「若 \(n^2\) 為偶數,則 \(n\) 為偶數」為真。
而上述證明方法是間接證法的一種,有時又被稱為反證法。
綜言之,利用 \(P\Rightarrow Q\) 與 \(\neg Q \Rightarrow \neg P\) 在邏輯上等價,因此,若證明了「\(\neg Q \Rightarrow \neg P\)」為真,則相當於證明了「\(P\Rightarrow Q\)」為真。
參考文獻:
- 齊斯.德福林(Keith Devlin)著(洪萬生、黃俊瑋等譯),《這個問題,你用數學方式想過嗎?》。


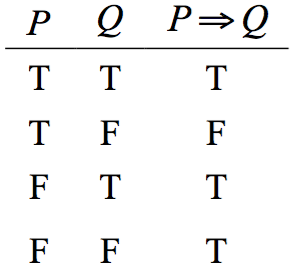
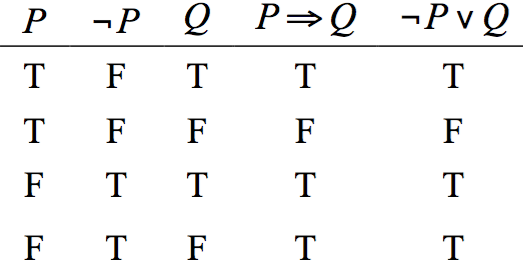
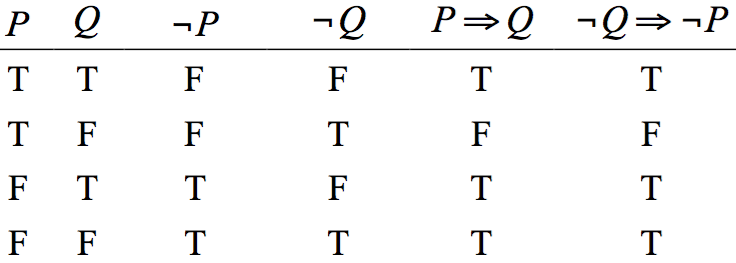
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria) 
