西方行列式的發展:范德蒙的研究(The Development of Determinants in West: Vandermonde’s Work)
西方行列式的發展:范德蒙的研究
(The Development of Determinants in West: Vandermonde’s Work)
國立臺南第一高級中學林倉億老師
范德蒙1772年提交法國科學院的論文〈關於消去法的報告〉(Mémoire sur l’Élimination)是數學家首度將行列式運算作為研究主題的論文。范德蒙一開始就對他的符號給出了定義 (見圖一):
\(\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ b \end{array}\; – \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ a \end{array}\)
\(\left. {\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\frac{{\,\beta \,}}{{\,c\,}}} \right|\frac{{\,\gamma \,}}{{\,a\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ c \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,a\,}}} \right|\frac{{\,\gamma \,}}{{\,b\,}}\)
\(\begin{array}{ll} \left. {\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}}} \right|\left. {\frac{{\,\gamma \,}}{{\,c\,}}} \right|\frac{{\,\delta \,}}{{\,d\,}} &= \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\left. {\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}}} \right|\frac{{\,\delta \,}}{{\,d\,}}\; – \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\left. {\frac{{\,\beta \,}}{{\,c\,}}} \right|\frac{{\,\gamma \,}}{{\,d\,}}} \right|\frac{{\,\delta \,}}{{\,a\,}}\; \\&+\;\begin{array}{*{20}{c}} \alpha \\ c \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\left. {\frac{{\,\beta \,}}{{\,d\,}}} \right|\frac{{\,\gamma \,}}{{\,a\,}}} \right|\frac{{\,\delta \,}}{{\,b\,}}\; – \;\begin{array}{*{20}{c}} \alpha \\ d \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\left. {\frac{{\,\beta \,}}{{\,a\,}}} \right|\frac{{\,\gamma \,}}{{\,b\,}}} \right|\frac{{\,\delta \,}}{{\,c\,}}\\ \;\;\;\; \vdots \\ \;\;\;\; \vdots \end{array}\)
我們現在習慣將足碼左右並列寫在下標,范德蒙則是直接將足碼上下表示,
所以,\(\begin{array}{*{20}{c}} \alpha \\ a \end{array}\) 要解讀成今日行列式的第 \(\alpha\) 列第 \(a\) 行之元。
因此,我們可以將范德蒙的符號 \(\frac{{\left. {\alpha \;} \right|\;\beta }}{{\left. {a\;} \right|\;b}}\) 視為只寫出主對角線之元的行列式 \(\left| {\,\begin{array}{*{20}{c}} {{t_{\alpha a}}}&{}\\ {}&{{t_{\beta b}}} \end{array}\,} \right|\),
主對角線確立後,其餘各元的足碼也可以隨之確定了
(第一、二列的第一個足碼分別都是 \(\alpha\) 與 \(\beta\),第一、二行的第二個足碼則分別都是 \(a\) 與 \(b\)),
即 \(\frac{{\left. {\alpha \;} \right|\;\beta }}{{\left. {a\;} \right|\;b}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ b \end{array}\; – \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ a \end{array}\)
用今日的行列式符號來表示就是 \(\left| {\,\begin{array}{*{20}{c}} {{t_{\alpha a}}}&{{t_{\alpha b}}}\\ {{t_{\beta a}}}&{{t_{\beta b}}} \end{array}\,} \right| = {t_{\alpha a}} \cdot {t_{\beta b}} – {t_{\alpha b}}{t_{\beta a}}\)。
在 \(\left. {\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\frac{{\,\beta \,}}{{\,c\,}}} \right|\frac{{\,\gamma \,}}{{\,a\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ c \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,a\,}}} \right|\frac{{\,\gamma \,}}{{\,b\,}}\) 的情形中,
若我們將 \(\alpha\) 與 \(a\) 代為 \(1\),\(\beta\) 與 \(b\) 代為 \(2\),\(\gamma\) 與 \(c\) 代為 \(3\),
則 \(\left. {\left. {\frac{{\,1\,}}{{\,1\,}}} \right|\frac{{\,2\,}}{{\,2\,}}} \right|\frac{{\,3\,}}{{\,3\,}} = \begin{array}{*{20}{c}} 1\\ 1 \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,2\,}}{{\,2\,}}} \right|\frac{{\,3\,}}{{\,3\,}}\; + \;\begin{array}{*{20}{c}} 1\\ 2 \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\frac{{\,2\,}}{{\,3\,}}} \right|\frac{{\,3\,}}{{\,1\,}}\; + \;\begin{array}{*{20}{c}} 1\\ 3 \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,2\,}}{{\,1\,}}} \right|\frac{{\,3\,}}{{\,2\,}}\)
就是今日三階行列式依第一列降階展開的結果,
即 \(\left| {\,\begin{array}{*{20}{c}} {{t_{11}}}&{{t_{12}}}&{{t_{13}}}\\ {{t_{21}}}&{{t_{22}}}&{{t_{23}}}\\ {{t_{31}}}&{{t_{32}}}&{{t_{33}}} \end{array}\,} \right| = {t_{11}}\left| {\,\begin{array}{*{20}{c}} {{t_{22}}}&{{t_{23}}}\\ {{t_{32}}}&{{t_{33}}} \end{array}\,} \right| + {t_{12}}\left| {\,\begin{array}{*{20}{c}} {{t_{23}}}&{{t_{21}}}\\ {{t_{33}}}&{{t_{31}}} \end{array}\,} \right| + {t_{13}}\left| {\,\begin{array}{*{20}{c}} {{t_{21}}}&{{t_{22}}}\\ {{t_{31}}}&{{t_{32}}} \end{array}\,} \right|\)
平心而論,范德蒙的符號確實是比今日的行列式符號簡潔,在降階展開的操作上,也十分便捷。
范德蒙展開的方法只有兩個簡單的步驟:
(1) 以三階為例,第一步是寫出 \(\begin{array}{*{20}{c}} 1\\ {} \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,2\,}}{{\,\,}}} \right|\frac{{\,3\,}}{{\,\,}}\),然後下方依序填入 \(123\)、\(231\)、\(312\),每次都將數字往前移動一位,而最左邊的數字則移到最右邊,直至重複為止。
(2) 決定每一項的運算符號,偶數階的展開是 \(+ – + – + -\cdots\),奇數階則統統為 \(+\)。
讀者不妨分別用范德蒙的與今日的符號展開四階行列式,然後再比較兩者的優缺點。
有了符號與定義後,范德蒙開始推導相關的性質與公式。
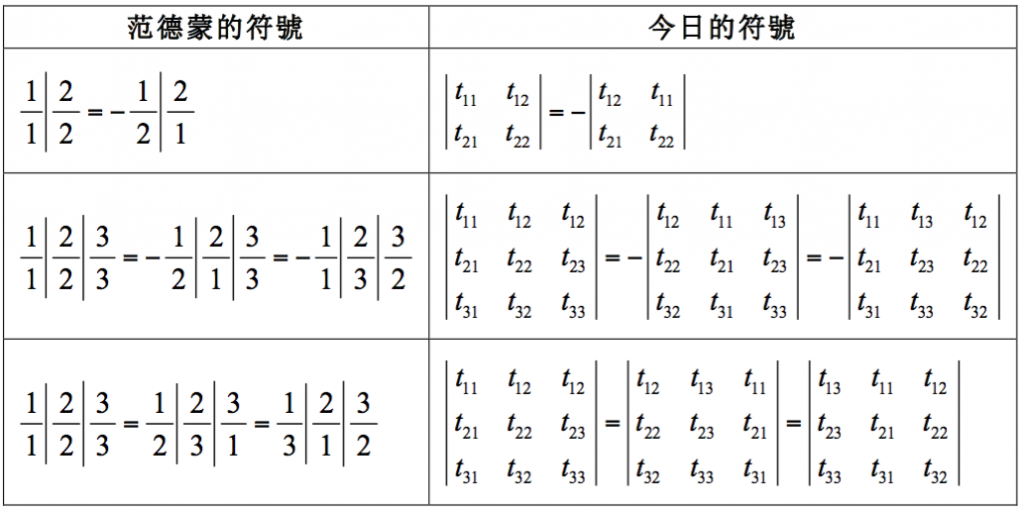
比如說,「行列式中任兩行互換,其值差一個負號」:
又如「行列式中任兩行或任兩列相同,其值為0」:
范德蒙在推出需要的公式後,才將他的符號應用到方程組的求解,
寫出今日所謂的「克拉瑪公式」(見圖二、圖三):
我們可以清楚地看到,范德蒙的公式和今日的公式只差在符號的不同,但就一般性或抽象化的程度來說,和今日的版本是一致的。雖然范德蒙只寫出二階與三階的克拉瑪公式,但其方法可以推廣,且更重要的是,可以簡潔地表示任意高階的克拉瑪公式,這比起前人來說(參閱本網站克拉瑪公式的相關文章),實在是一大進步。
范德蒙這篇論文共有17頁,到克拉瑪公式恰好佔了一半的篇幅。剩下的內容,范德蒙繼續推導相關的公式、提出不同的行列式展開式求法,並將研究的目標轉向高次方程組的求解。這剩下的部分,就留給有興趣的讀者自己研究了。
最後,請各位讀者再將目光回到圖三,筆者在〈西方行列式的發展:范德蒙的生平(2)〉一文中有提到,「范德蒙行列式」這名稱是個美麗的錯誤,而圖三,很可能就是這美麗錯誤的源頭。
若我們將圖三中方程組的係數寫成一個行列式,就會得到 \(\left| {\,\begin{array}{*{20}{c}} {_1^1}&{_2^1}&{_3^1}\\ {_1^2}&{_2^2}&{_3^2}\\ {_1^3}&{_2^3}&{_3^3} \end{array}\,} \right|\),
勒貝格 (Henri Léon Lebesgue, 1875-1941)推測後人很可能就是將上面的足碼理解成指數,
得到 \(\left| {\,\begin{array}{*{20}{c}} {{t_1}^1}&{{t_2}^1}&{{t_2}^1}\\ {{t_1}^2}&{{t_2}^2}&{{t_3}^2}\\ {{t_1}^3}&{{t_2}^3}&{{t_3}^3} \end{array}\,} \right| = {t_1} \cdot {t_2} \cdot {t_3} \cdot \left| {\,\begin{array}{*{20}{c}} 1&1&1\\ {{t_1}}&{{t_2}}&{{t_3}}\\ {{t_1}^2}&{{t_2}^2}&{{t_3}^2} \end{array}\,} \right|\),
如此一來,今日所稱的「范德蒙行列式」就現身了,即 \(\left| {\,\begin{array}{*{20}{c}} 1&1&1\\ {{t_1}}&{{t_2}}&{{t_3}}\\ {{t_1}^2}&{{t_2}^2}&{{t_3}^2} \end{array}\,} \right|\)。
參考文獻:
- Vandermonde, Alexandre-Théophile (1772). “Mémoire sur l’Élimination”, http://visualiseur.bnf.fr/Visualiseur?O=30000000035711
- Ycart, Bernard and Kuntzmann, Laboratoire Jean (2013). “A case of mathematical eponymy: the Vandermonde determinant”, Revue d’Histoire des Mathématiques, 9(1), pp.43-77.( http://hal.archives-ouvertes.fr/docs/00/68/99/43/PDF/VD_BY.pdf)
- 楊浩菊 (2004). 《行列式理論歷史研究》,西北大學博士論文。


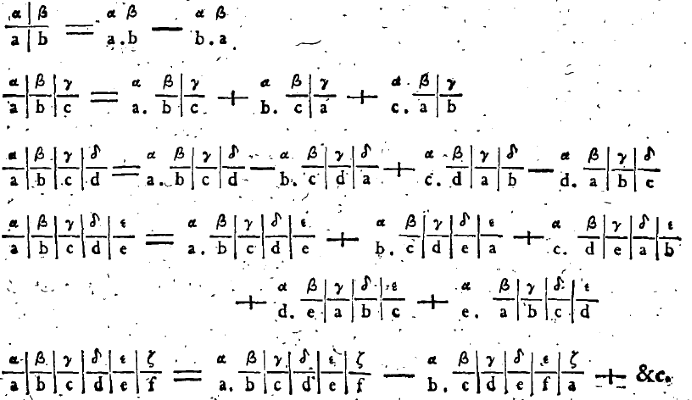


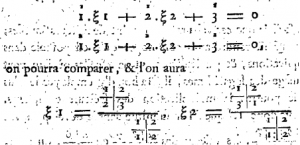
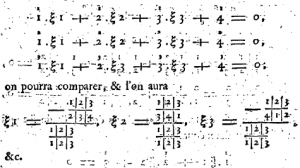
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題 
