牛頓插值多項式 (1)

牛頓插值多項式 (1) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師

由於多項式「常被用來逼近一般函數，並用來求一般函數的近似值。」，使得插值多項式有了學習的正當性，99課綱並特意引進拉格朗日插值多項式。

例如：以給定平面上三點 \(A(1,7),B(2,6),C(3,11)\) 為例，求圖形通過這三點的二次多項式。上述的問題等同於求一個二次多項函數 \(f(x)\)，使得 \(f(1)=7,f(2)=6,f(3)=11\)。

那麼，滿足條件的拉格朗日插值多項式為

\(\displaystyle f(x) = 7 \cdot \frac{{(x – 2)(x – 3)}}{{(1 – 2)(1 – 3)}} + 6 \cdot \frac{{(x – 1)(x – 3)}}{{(2 – 1)(2 – 3)}} + 11 \cdot \frac{{(x – 1)(x – 2)}}{{(3 – 1)(3 – 2)}}\)。

然而，許多課本還加碼補充牛頓插值多項式的方法（這也說明有著各種不同形式的插值多項式）。

通常開頭就會寫道：假設基於牛頓插值多項式，

滿足條件之函數 \(f(x)=f(1)+a(x-1)+b(x-1)(x-2)\)，

再將 \(f(2)=6,f(3)=11\) 代入，求出 \(a,b\)。

事實上，這樣的補充留下的問題，比它所解決的問題還多。例如，為何牛頓插值多項式會是上述的形式？除了背誦記憶規則外，有沒有理解它的其他方法？牛頓插值多項式的假設仍需要再求解未知數，會比拉格朗日插值多項式便利嗎？這個方法最早是牛頓給出的嗎？他如何想到的？是為了解決什麼問題呢？這個系列文章就是想要解答以上這些問題。首先，就由牛頓開始吧！

1687年，牛頓的《自然哲學的數學原理》(Philosophiæ Naturalis Principia Mathematica)拉丁版首次印行，牛頓在書中試圖從各個運動現象探究原因，並試圖用來解釋天文觀測的運動現象。書中提出我們所熟知的牛頓運動定律，奠定古典力學的基礎，也發表了萬有引力定律。此書從定義、公理、或運動的定律出發，推導出命題，就能看出深受《幾何原本》公理化體系的影響。無疑地，牛頓透過這樣的知識架構塑造《自然哲學的數學原理》的地位，並且透過數學的推論來支持命題的說明。有關牛頓插值法的內容發表在第三編〈宇宙體系〉的引理五：求通過任意點的拋物線類曲線(見圖一)。其目的是為了解決引理六的問題：已知彗星的某些觀測位置，求彗星在任意給定時刻的位置。

圖一\(~~~\)《自然哲學的數學原理》(1687年拉丁版) 書影 下載自http://www.ntnu.no/ub/spesialsamlingene/ebok/02a019654.html

事實上，從圖一清楚可見，牛頓沒有使用多項式的術語，純然運用幾何術語，將某些幾何量予以加減處理的規律，會何被認為得出插值多項式的各項係數？同時，他也沒有對方法的正確性多作說明。倒是1795年，拉格朗日在巴黎的一場演講中，對牛頓的作法做了一番解釋。據林倉億的看法，他認為拉格朗日插值多項式的原始想法可能是來自他對牛頓插值多項式的研究，請參見林倉億，〈牛頓插值多項式：拉格朗日怎麼說？〉一文。此處，作者試圖借助現代數學符號的輔助，說明牛頓提出的作法之結果。

為了簡化表示，容筆者先介紹數值分析中有關「均差」的概念和符號。

設函數 \(f(x)\) 有 \(n+1\) 個相異點 \(({x_0},f({x_0})),({x_1},f({x_1})),({x_2},f({x_2})),\cdots,({x_n},f({x_n}))\)。

則定義一階均差及符號為 \(\frac{{f({x_i}) – f({x_j})}}{{{x_i} – {x_j}}} = f[{x_i},{x_j}]\)，其中 \(i\ne j\)。

例如 \(\frac{{f({x_0}) – f({x_1})}}{{{x_0} – {x_1}}} = f[{x_0},{x_1}]\)。

同理，定義二階均差為一階均差的均差 \(\frac{{f[{x_i},{x_j}] – f[{x_j},{x_k}]}}{{{x_i} – {x_k}}} = f[{x_i},{x_j},{x_k}]\)，

例如 \(\frac{{f[{x_1},{x_2}] – f[{x_2},{x_3}]}}{{{x_1} – {x_3}}} = f[{x_1},{x_2},{x_3}]\)。

類推下去，不難想像 \(n\) 階均差應為 \(n-1\) 階均差的均差

\(\displaystyle f[{x_0},{x_1}, \cdots ,{x_n}] = \frac{{f[{x_0},{x_1}, \cdots ,{x_{n – 1}}] – f[{x_1},{x_2}, \cdots ,{x_n}]}}{{{x_0} – {x_n}}}\)。

好了，我們可以回頭來看牛頓的作法。

圖二

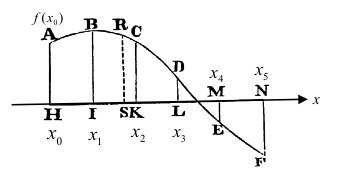
如圖二，牛頓假設這些點分別為 \(A,B,C,D,E,F\)，

並分別作這些點的垂線 \(AH,BI,CK,DL,EM,FN\) 到任意給定的直線 \(HN\)（設為 \(x\) 軸），

垂足分別為 \(H,I,K,L,M,N\)。

接著，牛頓分成 \(HI,IK,KL,LM,MN\) 這些間隔都等長，以及不等長的兩種情形分別討論。

以下直接考慮不等長的一般情形，

設 \(H,I,K,L,M,N\) 各點的 \(x\) 坐標分別為 \(x_0,x_1,\cdots,x_5\)，

則 \(A({x_0},f({x_0}))\)，\(B({x_1},f({x_1}))\)，\(C({x_2},f({x_2}))\)，\(D({x_3},f({x_3}))\)，\(E({x_4},f({x_4}))\)，\(F({x_5},f({x_5}))\)。

若 \(S\) 點的坐標為 \(x\)，其目的是要求出 \(RS=f(x)\) 之值。

首先，考慮 \(AH,BI,CK,DL,EM,FN\) 彼此的長度差與 \(HI,IK,KL,LM,MN\)

這些間隔的比值

\(\frac{{AH – BI}}{{HI}} = b = \frac{{f({x_0}) – f({x_1})}}{{{x_1} – {x_0}}} =- f[{x_0},{x_1}]\);

\(\frac{{BI – CK}}{{IK}} = 2b = \frac{{f({x_1}) – f({x_2})}}{{{x_2} – {x_1}}} =- f[{x_1},{x_2}]\);

\(\frac{{CK – DL}}{{KL}} = 3b = \frac{{f({x_2}) – f({x_3})}}{{{x_3} – {x_2}}} =- f[{x_2},{x_3}]\)；

\(\frac{{DL + EM}}{{ML}} = 4b = \frac{{f({x_3}) + ( – f({x_4}))}}{{{x_4} – {x_3}}} = \frac{{f({x_3}) – f({x_4})}}{{{x_4} – {x_3}}} =- f[{x_3},{x_4}]\)；

\(\frac{{ – EM + FN}}{{NM}} = 5b = \frac{{ – ( – f({x_4})) + ( – f({x_5}))}}{{{x_5} – {x_4}}} = \frac{{f({x_4}) – f({x_5})}}{{{x_5} – {x_4}}} =- f[{x_4},{x_5}]\)。[1]

牛頓稱這些 \(b\) 為「一次差」，

接著就是「二次差」\(\frac{{b – 2b}}{{HK}} = c = \frac{{ – f[{x_0},{x_1}] – ( – f[{x_1},{x_2}])}}{{{x_2} – {x_0}}} = f[{x_0},{x_1},{x_2}]\)；\(\frac{{2b – 3b}}{{IL}} = 2c = f[{x_1},{x_2},{x_3}]\)。

同理，「三次差」\(d = \frac{{c – 2c}}{{HL}} =- f[{x_0},{x_1},{x_2},{x_3}]\)，

「四次差」\(e = \frac{{d – 2d}}{{HM}} = f[{x_0},{x_1},{x_2},{x_3},{x_4}]\)，

「五次差」\(f = \frac{{e – 2e}}{{HN}} =- f[{x_0},{x_1},{x_2},{x_3},{x_4},{x_5}]\)。

找出這些差之後，再令 \(AH = a = f({x_0})\)，\(p =- HS = ({x_0} – x)\)，

\(q = p \times ( – IS) = ({x_0} – x)({x_1} – x) = (x – {x_0})(x – {x_1})\)，

\(r = q \times ( + SK) = (x – {x_0})(x – {x_1})({x_2} – x) =- (x – {x_0})(x – {x_1})(x – {x_2})\)，

\(\begin{array}{ll} s &= r \times ( + SL) =- (x – {x_0})(x – {x_1})(x – {x_2})({x_3} – x) \\&=(x – {x_0})(x – {x_1})(x – {x_2})(x – {x_3})\end{array}\)，

\(\begin{array}{ll} t &= s \times ( + SM) = (x – {x_0})(x – {x_1})(x – {x_2})(x – {x_3})({x_4} – x) \\&=- (x – {x_0})(x – {x_1})(x – {x_2})(x – {x_3})(x – {x_4})\end{array}\)

其中，在 \(S\) 到 \(A\) 的各項 \(HS,IS\) 要加負號；另一側的項 \(SK,SL,SM\) 則加正號。

如此一來，就能寫出 \(RS\) 的值：

\(\begin{array}{ll}RS &= f(x) = a + bp + cq + dr + es + ft + … \\&= f({x_0}) + f[{x_0},{x_1}](x – {x_0}) + f[{x_0},{x_1},{x_2}](x – {x_0})(x – {x_1})\\& + f[{x_0},{x_1},{x_2},{x_3}](x – {x_0})(x – {x_1})(x – {x_2}) + f[{x_0},{x_1},{x_2},{x_3},{x_4}](x – {x_0})(x – {x_1})(x – {x_2})(x – {x_3}) \\&+ f[{x_0},{x_1},{x_2},{x_3},{x_4},{x_5}](x – {x_0})(x – {x_1})(x – {x_2})(x – {x_3})(x – {x_4})\end{array}\)

這個結果讓我們看到牛頓插值多項式的形式，

事實上，這與與現行數值分析中所談的牛頓插值多項式完全吻合。

做個練習，讓我們更加掌握牛頓插值多項式，就以本文開頭的例子

求一個二次多項函數 \(f(x)\)，使得 \(f(1)=7,f(2)=6,f(3)=11\)。

由上述可知，找一次差 \(f[1,2]=\frac{7-6}{1-2}=-1\)；\(f[2,3]=\frac{6-11}{2-3}=5\)，

二次差 \(f[1,2,3] = \frac{{( – 1) – 5}}{{1 – 3}} = 3\)。

因此所求函數為 \(f(x) = f(1) – (x – 1) + 3(x – 1)(x – 2)\)。

同時，相信細心的你也發現牛頓插值多項式的係數直接就能求得，我們將在〈牛頓插值多項式(3)〉有更詳盡的介紹。此外，牛頓並沒有留下任何線索提示我們他是如何得到這個形式，在下一篇〈牛頓插值多項式(2)〉中，我們試圖以多項式的知識對此給出一個教學上適切的引導。

連結：牛頓插值多項式(2)

參考文獻

• 《自然哲學的數學原理》線上閱讀http://en.wikisource.org/wiki/The_Mathematical_Principles_of_Natural_Philosophy_(1846)/BookIII-Prop6
• 林倉億，〈牛頓插值多項式：拉格朗日怎麼說？〉，《HPM通訊》第15卷第10期(2012)：頁1-7。

[1]此處牛頓使用的彼此並無關係。同理，也是相同情形。