過圓上一點求切線（一） （Finding the tangent line through a point on a circle Ⅰ）

過圓上一點求切線（一）（Finding the tangent line through a point on a circle Ⅰ）
國立臺灣師範大學數學所博士班黃俊瑋

高二上圓與直線相關單元裡，除了介紹平面上的圓與直線的方程式之外，也進一步利用方程式討論了圓與直線的關係。其中，當直線與圓相切時，又衍生出三類常見求切線問題：1.過圓上一點求切線、2.過圓外一點求切線，以及3.求已知斜率之切線。

本文主要聚焦在第一類過圓上一點求切線問題上，一方面提供多類解法，並說明該解法能否推廣用於其它兩類問題，以及能否推廣至拋物線、橢圓與雙曲線相關求切線問題上（現今高中課程有關三類圓錐曲線的求切線問題已刪除，因此，這部份筆者僅略述之）。

舉例來說，問題如下：

「已知坐標平面上一圓之方程式為 \((x-1)^2+(y-2)^2=5\)，
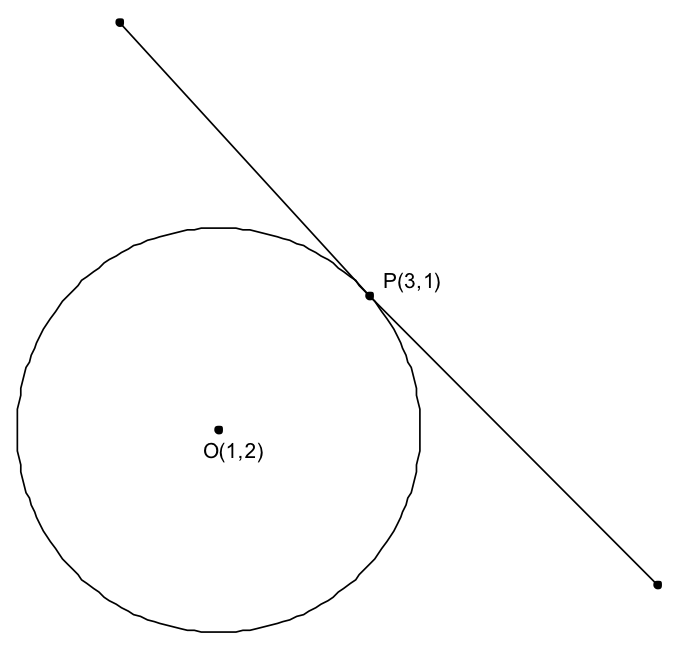
求過此圓上一點 \(P(3,1)\) 的切線方程式（如圖一所示）。」

針對這個問題，教科書中提供了相關公式解，

過圓 \({(x – h)^2} + {(y – k)^2} = {r^2}\) 上一點 \(P(x_0,y_0)\) 的切線為：

\(({x_0} – h)(x – h) + ({y_0} – k)(y – k) = {r^2}\)

特別地，當圓心在原點時，過圓 \(x^2+y^2=r^2\) 上一點 \(P(x_0,y_0)\) 的切線公式更可簡化為：

\(x_0x+y_0y=r^2\)

因此，過上述圓上 \(P(3,1)\) 點的切線為 \((3 – 1)(x – 1) + (1 – 2)(y – 2) = 5\)，

即 \(2x-y=5\)。

圓一\(~~~\)過圓 \({(x – 1)^2} + {(y – 2)^2} = 5\) 上一點 \(P(3,1)\) 求切線

類似的公式可用於求解「過一般二次曲線上任一點求切線問題」：
過二次曲線 \(\Gamma :a{x^2} + b{y^2} + cx + dy + e = 0\) 上一點 \(P(x_0,y_0)\) 的切線為：

 \(a{x_0}x + b{y_0}y + c\frac{{{x_0} + x}}{2} + d\frac{{{y_0} + y}}{2} + e = 0\)

換言之，包含拋物線、橢圓與雙曲線等各類二次曲線都適用於此類公式。除了公式解之外，筆者整理了其它方法，供讀者參考。

方法1利用切點至圓心連線與切線垂直

方法1-1　

如圖一所示，因為圓心至切點之連線段 \(OP\) 垂直切線，

又直線 \(\leftrightarrow{OP}\) 之斜率 \(m_{\leftrightarrow{OP}} = \frac{{1 – 2}}{{3 – 1}} = \frac{{ – 1}}{2}\)，

因此，切線之斜率 \(m=2\)，故可設切線為 \(y=2x+k\)。

又 \(P(3,1)\) 在切線上，代入可得 \(k=-5\)，即切線為 \(y=2x-5\)。

方法1-2

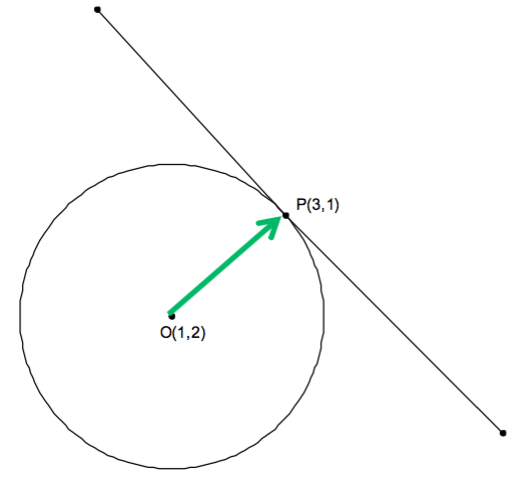
如圖二所示，因為圓心至切點之連線段 \(OP\) 與所求切線垂直，

因此向量 \(\vec{OP}=(2,-1)\) 為切線之法向量，可假設切線為 \(2x-y=k\)。

又 \(P(3,1)\) 在切線上，代入可得 \(k=5\)，即切線為 \(2x-y=5\)。

圖二\(~~~\vec{OP}=(2,-1)\) 與直線方向向量垂直

方法1-3

如圖二所示，因為圓心至切點之連線段 \(OP\) 與切線垂直，

因此可取與向量 \(\vec{OP}=(2,-1)\) 垂直的向量 \(\vec{L}=(1,2)\) 作為切線方向向量。

因此，可得切線之參數式為 \(\left\{ {\begin{array}{*{20}{c}} {x = 2t + 3}\\ {y = – 1t + 1} \end{array}} \right.\)，其中 \(t\in \mathbb{R}\)

方法1-4

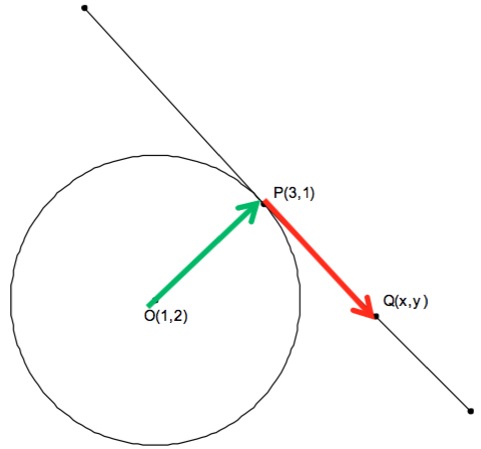
設 \(Q(x,y)\) 為直線 \(L\) 上一動點，則向量 \(\vec{PQ}=(x-3,y-1)\)。

因為圓心至切點之連線段OP與切線垂直，

因此，向量 \(\vec{OP}=(2,-1)\) 與向量 \(\vec{PQ}=(x-3,y-1)\) 內積之值為 \(0\)，

可得 \(2(x-3)-1(y-1)=0\)，即可得切線為 \(2x-y=5\)。

圖三\(~~~\vec{OP}=(2,-1)\) 與 \(\vec{PQ}=(x-3,y-1)\) 垂直

評析：這類法方主要利用國中階段所學過，「切點至圓心連線與切線垂直」這個性質，再搭配直線的斜率、垂直直線的斜率關係、垂直向量的關係以及直線的法向量或方向量等，直接造出所求之切線。

其中，方法1-1所需概念簡單，教科書一般便是利用此方法，推導出前述公式解。而此類方法中的另3個方法，則需引入向量的概念，但都不失簡易性。不過，此類方法雖簡易，卻僅限於「過圓上一點求切線」這類問題，並無法推廣至其它的二次曲線問題。  

方法2 判別式法

利用點斜式可假設過 \(P(3,1)\) 之切線方程式為 \(y-1=m(x-3)\)，

因為直線與圓相切，因此聯立方程式 \(\left\{ {\begin{array}{*{20}{c}} {{{(x – 1)}^2} + {{(y – 2)}^2} = 5}\\ {y – 1 = m(x – 3)} \end{array}} \right.\) 恰有一組解（重根），

解此方程組的過程，可得 \({(x – 1)^2} + {[m(x – 3) + 1 – 2]^2} = 5\)，展開整理後可得方程式：

\(({m^2} + 1){x^2} + ( – 6{m^2} – 2m – 2)x + 9{m^2} + 6m – 3 = 0\)

因為此方程式有重根，所以其判別式為 \(0\)，即：

\({( – 6{m^2} – 2m – 2)^2} – 4({m^2} + 1)(9{m^2} + 6m – 3) = 0\)

最後可解出 \(m=2\)。則 \(y-1=2(x-3)\) 即為所求之切線。

評析：這是高中課程中所介紹的標準方法。不過，當讀者實際動手試算後，不難發現，這個方法無論是計算過程或代數運算上，皆遠較其它方法來得複雜且冗長。不過，此方法適用於各類與圓相關的求切線問題，同時也可進一步通用於其它二次曲線求切線問題上。

當我們適當假設切線後，將二次曲線與切線聯立可得：

\(\left\{ {\begin{array}{*{20}{c}} {\Gamma :a{x^2} + b{y^2} + cx + dy + e = 0}\\ {L:y – {y_0} = m(x – {x_0})} \end{array}} \right.\)

整理後可得 \(x\) 的二次式：\(Ax^2+Bx+C=0\) 或 \(y\) 的二次式：\(Ay^2+By+C=0\)
再利用相切的關係，可知上述二次方程式有重根，其判別式為 \(0\)，如此可解出所求的切線斜率。換言之，雖然此方法整個代數操作過程冗長，但極具一般性，可通用於相關求切線問題。

本文所介紹的各類解法，皆屬於高二課程的範疇，接著，在〈過圓上一點求切線（二）〉介紹另外三種方法，最後簡單統整各種方法所適用的問題。

連結：過圓上一點求切線（二）