定壓熱容量（Cp）和定容熱容量（Cv）的差別（下）

定壓熱容量（Cp）和定容熱容量（Cv）的差別（下）
國立臺灣師範大學化學系兼任教師邱智宏

連結：定壓熱容量（Cp）和定容熱容量（Cv）的差別（上）

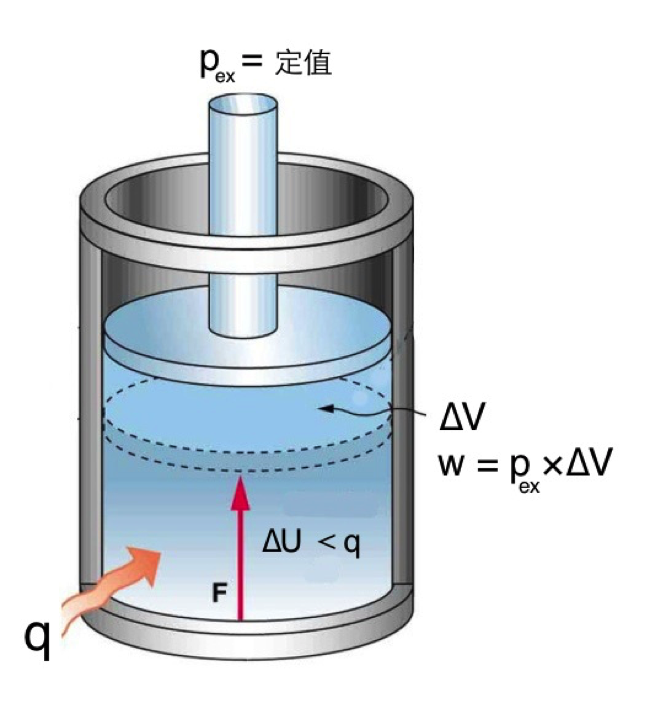
有了上篇 \(C_V\) 的測量基礎，為了更易於了解，我們先以氣體為例，若測定一定量氣體的 \(C_V\)，其升高 \(1~K\) 所需的內能變化\((\Delta U)\)，由於没有對外作功，其情況顯然和定壓下升高 \(1~K\)，焓的變化量\((\Delta H)\)有所不同，如圖二所示：當系統在等壓情況下，吸收定量的熱時，除了系統的內能會增加，系統內的溫度因而上升，使容器內壓力加大向上膨脹，對外作功，直至內壓等於外壓\((p_{ex})\)時停止。此時系統對外做功\((w=p_{ex}\times \Delta V)\)，因此系統吸收的總熱量\((q)\)，有一部分要用來對外作功，所以系統增加的內能\((\Delta U)\)將小於 \(q\)。

據此，等量的物質，在定壓下系統上升 \(1~K\)，所吸收的熱量\((q_p)\)，要比在定容下上升 \(1~K\) 所需的熱量\((q_c)\)還要多，因此在氣態的物質中，\(C_p\) 恒大於 \(C_V\)。

圖二\(~~~\)定壓下加熱系統，由於物質體積膨脹 \(\Delta V\)，系統需對外作功\((w)\)，其定壓之熱容量大於定容的熱容量。

三、\(C_p\) 和 \(C_V\) 相差多少

若直接將 \(C_p\) 和 \(C_V\) 相減，\(C_p-C_V=(\frac{\partial H}{\partial T})_p-(\frac{\partial U}{\partial T})_V\)，並將 \(H=U+pV\) 代入

\(C_p-C_V=(\frac{\partial U}{\partial T})_p+(\frac{\partial (pV)}{\partial T})_p-(\frac{\partial U}{\partial T})_V~~~~~~~~~(8)\)

上式中，「定壓下」內能隨溫度的變化率，減定容下內能隨溫度的變化率：\((\frac{\partial U}{\partial T})_p-(\frac{\partial U}{\partial T})_V\)，代表什麼意義？

若由 \((2)\) 式開始推導，並在定壓下，以溫度對 \((2)\) 式微分可得 \((9)\) 式

\(\mathrm{d}U=C_V\mathrm{d}T+\pi_T\mathrm{d}V~~~~~~~~~(2)\)

\((\frac{\partial U}{\partial T})_p=C_V+\pi_T(\frac{\partial V}{\partial T})_p~~~~~~~~~(9)\)

其中 \((\frac{\partial U}{\partial T})_p\)，代表在定壓下，溫度改變對體積的影響，

一般以膨脹係數\((\alpha)\)表示，\(\alpha=\frac{1}{V}(\frac{\partial V}{\partial T})_p\)，

另外 \(C_V=(\frac{\partial U}{\partial T})_V\)，將此二者代入 \((9)\) 式，並適當移項

\((\frac{\partial U}{\partial T})_p-(\frac{\partial U}{\partial T})_V=\pi_T\alpha V\)

將結果代入 \((8)\) 式：\(C_p-C_V=\pi_T\alpha V+(\frac{\partial (pV)}{\partial T})_p\)，

其中最後一項，因 \(p\) 為定值，\((\frac{\partial (pV)}{\partial T})_p=p(\frac{\partial V}{\partial T})_p=p\alpha V\)

\(C_p-C_V=\pi_T\alpha V+p\alpha V~~~~~~~~~(10)\)

上式中 \(\alpha V\) 為系統於溫度改變時體積的變化率，\(p\alpha V\) 則為溫度改變時系統作功的量，

因此影響 \(C_p\) 和 \(C_V\) 差別的第一個因素，即為 \(C_p\) 需對外作功，而 \(C_V\) 為定容則否。

第二個因素為 \(\pi_T\alpha V\) 則較為複雜，

\(\pi_T=(\frac{\partial U}{\partial V})_T\) 為系統在定溫下，改變體積對系統內能的影響，

例如氣體分子間彼此有吸引力，如果增大體積時則須提供能量，以迫使分子分開。

以下探討三種不同的情況：

1. 如果是理想氣體的情況，分子間並不存在任何引力，因此 \(\pi_T=0\)，即增大體積對系統的內能没有影響。據此 \((10)\) 式可改寫如下(由於 \(pV=nRT\)，\((\frac{\partial V}{\partial T})_p=\frac{1}{p}(\frac{\partial (nRT)}{\partial T})_p=\frac{nR}{p}\))
   \(C_p-C_V=p\alpha V=p(\frac{\partial V}{\partial T})_p=p\frac{nR}{p}=nR~~~~~~~~~(11)\)
2. 如果不是理想氣體時，\(\pi_T\ne 0\)，\(C_p\) 和 \(C_V\) 的差異就必須按照 \((10)\) 式來計算，\((11)\) 式僅為理想氣體的特殊情況，式 \((10)\) 才是通式。
3. 如果是固體或液體的情形，由於溫度的改變對於體積的改變不大，其 \(\alpha V\) 值很小，因此一般情況 \((10)\) 中的 \(C_p-C_V\approx 0\)，亦即兩者幾乎相等。

四、\(C_p/C_V=\gamma\) 的使用時機

\(\gamma\) 值通常在絕熱情況下，探討理想氣體在不同狀態，其 \(p\)、\(V\)、\(T\) 間的關係時才會使用到。

一般理想氣體若在等溫時，\(pV=\)定值，但若在絕熱、可逆的情況下則情況就不同，

假設體積由 \(V_i\) 改變為 \(V_f\)，則 \(V\) 與 \(p\) 和 \(T\) 間的變化有何關係式。

因為 \(\mathrm{d}U=\mathrm{d}q+\mathrm{d}w\)，在絕熱狀況下，因為 \(\mathrm{d}q=0\)，所以 \(\mathrm{d}U =\mathrm{d}w = -p\mathrm{d}V\)，

另外 \(\mathrm{d}U = C_V\mathrm{d}T\)，因此 \(C_V\mathrm{d}T=-p\mathrm{d}V\) ,

將 \(p = nRT/V\) 代入前式，共並移項整理可得：

\(C_V\frac{\mathrm{d}T}{T}=-nR\frac{\mathrm{d}V}{V}\)

兩邊積分：\(\int_{T_i}^{T_f}C_V\frac{\mathrm{d}T}{T}=\int_{V_i}^{V_f}-nR\frac{\mathrm{d}V}{V}\Rightarrow C_V\ln\frac{T_f}{T_i}=-nR\ln\frac{V_f}{V_i}\)

\((\frac{T_f}{T_i})^{C_V}=(\frac{V_i}{V_f})^{nR}~~~~~~~~~(12)\)

若將 \(T_i\) 和 \(T_f\) 藉 \(pV=nRT\)，換成 \(p_i\)、\(V_i\) 和 \(p_f\)、\(V_f\)，則式 \((12)\) 可化簡如下：

\((\frac{p_f}{p_i}\frac{V_f}{V_i})^{C_V}=(\frac{V_i}{V_f})^{nR}\Rightarrow (\frac{p_f}{p_i}\frac{V_f}{V_i})=(\frac{V_i}{V_f})^{\frac{nR}{C_V}}\Rightarrow (\frac{p_f}{p_i})=(\frac{V_i}{V_f})^{\frac{nR}{C_V}+1}\)

由式 \((12)\) 可知 \(C_V+nR=C_p\)，因此上式的 \((nR/C_V)+1=C_p/C_V\)，

若將 \(C_p/C_V=\gamma\)，則上式可表示如下：

\(p_fV_f^\gamma=p_iV_i^\gamma=\)定值\(~~~~~~~~~(13)\)

五、總結

由上列的推導可知，\(C_p\) 和 \(C_V\) 差異如式 \((10)\) 所列，\(C_p\) 除了必須對外作功以外 \((p\alpha V)\)，尚須克服分子間的引力 \((\pi_T\alpha V)\)，因此 \(C_p\) 在一般情況大於 \(C_V\)。式 \((10)\) 為通式，對於任何物質均適用，若使用在特殊情況下，例如理想氣體，由於分子間無引力存在，因此 \(C_p\) 和 \(C_V\) 間的差異，就如式 \((11)\) 所示，相差 \(nR\)，如果是真實氣體，式 \((11)\) 便不適用，必須再經由式 \((10)\) 推導。

另外，在固體或液體的情形，由於溫度的改變對於體積的改變不大，其 \(\alpha\) 值很小，例如水為 \(2.1\times 10^{-4}K^{-1}\)、鑽石為 \(3.0\times 10^{-6}K^{-1}\)，因此 \(C_p-C_V\approx 0\)，亦即兩者幾乎相等。

最後，對於一般甫上化學熱力學的學子而言，常將 \(pV=constant\)，誤視為通式，殊不知理想氣體在絕熱、可逆的條件下，則必須 \(pV^\gamma=constant\)，方能成立，當然這也是一種特例，而不是通式。

參考資料

1. http://physiclessons.blogspot.tw/2012/11/blog-post_26.html
2. P. W. Atkins, “Physical Chemistry”, Oxford University Press, Oxford, 5th ed., p. 99~114 (1994).