數學之旅：三角形面積公式(II)

數學之旅：三角形面積公式(II)
(Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師

連結：數學之旅：三角形面積公式(I) 

4. 海龍公式：
   若 \(\Delta ABC\) 的三邊長 \(\overline {BC}= a,\overline {CA}= b,\overline {AB}= c\)，
   令 \(s = \frac{{a + b + c}}{2}\)，即三角形的半周長(semiperimeter)，
   則 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\)，此稱為海龍公式(Heron’s formula)。證明：
   一般高中數學教科書常用代數方法證明，即利用餘弦定理及兩次平方差公式，如下敘述。
   (強調一下這並不是海龍當時的證明)
   \(\begin{array}{ll}a\Delta ABC&= \frac{1}{2}bc\sin A = \frac{1}{2}\sqrt {{b^2}{c^2}{{\sin }^2}A}\\&=\frac{1}{2}\sqrt {{b^2}{c^2}(1 – {{\cos }^2}A)}\\&=\frac{1}{2}\sqrt {{b^2}{c^2} – {b^2}{c^2}{{\left( {\frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}} \right)}^2}}\\&=\frac{1}{2} \cdot \frac{1}{2}\sqrt {{{\left( {2bc} \right)}^2} – {{\left( {{b^2} + {c^2} – {a^2}} \right)}^2}}\\&= \frac{1}{4}\sqrt {\left[ {\left( {{b^2} + 2bc + {c^2}} \right) – {a^2}} \right]\left[ {{a^2} – \left( {{b^2} – 2bc + {c^2}} \right)} \right]}\\&=\frac{1}{4}\sqrt {\left[ {{{\left( {b + c} \right)}^2} – {a^2}} \right]\left[ {{a^2} – {{\left( {b – c} \right)}^2}} \right]}\\&=\frac{1}{4}\sqrt {\left( {a + b + c} \right)\left( {b + c – a} \right)(a + b – c)\left( {a + c – b} \right)}\\&=\frac{1}{4}\sqrt {2s\left( {2s – 2a} \right)\left( {2s – 2b} \right)\left( {2s – 2c} \right)}\\&=\sqrt {s\left( {s – a} \right)\left( {s – b} \right)(s – c)}\end{array}\)
   在一般數學教學現場中，學生對於海龍公式證明的反應，通常是認為繁瑣、難以心神領會；可是對於這個公式的方便又折服不已，因為只要給定三邊長就可以算出三角形面積，這是多麼美麗的公式(beautiful formula)啊！不過值得提醒的是，學生常會將海龍公式寫成 \(a\Delta ABC = \frac{1}{2}\sqrt {s(s – a)(s – b)(s – c)}\)，箇中道理當然是受「三角形面積等於底邊長乘於對應高的一半」的影響。海龍公式除了是計算題的妙計外，有時針對特殊的證明，往往具有畫龍點睛的效果。例如：證明當三角形的周長固定時，正三角形的面積最大。
   證明：
   因為周長固定，所以，\(s\) 為定值。
   利用算幾不等式 \(\frac{{(s – a) + (s – b) + (s – c)}}{3} \ge \sqrt[3]{{(s – a)(s – b)(s – c)}}\)，
   等號成立時，\(s – a = s – b = s – c\)，即 \(a=b=c\)，
   所以 \({\left( {\frac{s}{3}} \right)^3} \ge (s – a)(s – b)(s – c)\)，而 \(s = \frac{{a + b + c}}{2} = \frac{{3a}}{2}\)，
   得 \((s – a)(s – b)(s – c) \le {\left( {\frac{a}{2}} \right)^3}\)，
   代入海龍公式 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\le\sqrt {\frac{{3a}}{2}\cdot\frac{{{a^3}}}{8}}=\frac{{\sqrt 3 }}{4}{a^2}\)
   (此即為正三角形邊長為時的面積)。

   卡當諾(Girolamo Cardano, 1501-1576)所著的《偉大的技藝(Ars Magna，英譯為The Great art)》書中有一題有趣的三角形面積問題：(我就直譯為中文了)
   
   某三角形的第一邊比第二邊長 \(1\)，而第二邊又比第三邊長 \(1\)。若三角形的面積為 \(3\)，試求其三邊長。

   解法：
   假設三角形的三邊長為 \(x-1,x,x+1\)，
   根據海龍公式 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\)，
   因為  \(s = \frac{{(x – 1) + x + (x + 1)}}{2} = \frac{{3x}}{2}\)，代入得 \(3 = \sqrt {\frac{{3x}}{2} \cdot \frac{{x + 2}}{2} \cdot \frac{x}{2} \cdot \frac{{x – 2}}{2}}\)，
   左右平方得 \(9 = \frac{{3{x^2}}}{{16}}\left( {{x^2} – 4} \right)\)，化簡得 \({\left( {{x^2}} \right)^2} – 4({x^2}) – 48 = 0\)，
   配方得 \({\left( {{x^2} – 2} \right)^2} = 52\)，即 \({x^2} = 2\sqrt {13}+ 2\)，所以 \(x = \sqrt {2\sqrt {13}+ 2}\)，
   因此，三邊長 \(\sqrt{2\sqrt{13}+2}- 1,\sqrt {2\sqrt{13}+2} ,\sqrt{2\sqrt{13}+2}+1\)。

5. 三斜求積術：秦九韶(1208-1261)是南宋時的數學家，著有《數書九章》，此書有三大特色：大衍求一術、秦九韶演算法、三斜求積術。
   
   《數書九章》卷五題二云：「以小斜冪并大斜冪，減中斜冪，餘半之，同乘於上。以小斜冪并大斜冪，減上，餘四約之為實，開平方，得積。」
   以白話文闡述，若三角形的三斜邊以小、中、大稱之，
   則 ​\( 三角形面積=\sqrt{\frac{1}{4}\big[小^2\cdot大^2-\big(\frac{大^2+小^2-中^2}{2}\big)^2\big]} \)​ 。

   已知：若三角形的三斜邊小、中、大，分別以 \(a,b,c\) 表示。
   求證：\(a\Delta ABC = \sqrt {\frac{1}{4}\left[ {{a^2} \cdot {c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\)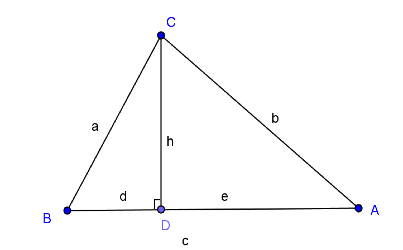
   證明：
   因為 \(\left\{ \begin{array}{l} c = d + e………\left( 1 \right)\\ {a^2} = {h^2} + {d^2}……\left( 2 \right)\\ b{}^2 = {h^2} + {e^2}……(3) \end{array} \right.\)，
   由 \((2)-(3)\) 得：\({a^2} – {b^2} = {d^2} – {e^2}\)，
   利用平方差得 \({a^2} – {b^2} = (d – e)(d + e) = c \cdot (d – e)\)，
   所以，\(d – e = \frac{{{a^2} – {b^2}}}{c}……(4)\)，
   由 \((1)+(4)\) 得：\(2d = c + \frac{{{a^2} – {b^2}}}{c} = \frac{{{c^2} + {a^2} – {b^2}}}{c}\)，因此，\(cd = \frac{{{c^2} + {a^2} – {b^2}}}{2}\)。
   \(\begin{array}{ll}a\Delta ABC &= \frac{1}{2}ch = \sqrt {\frac{1}{4}{c^2}{h^2}}\\&= \sqrt {\frac{1}{4}{c^2}({a^2} – {d^2})}\\&=\sqrt {\frac{1}{4}({a^2}{c^2} – {{(cd)}^2})}\\&=\sqrt {\frac{1}{4}\left[ {{a^2}{c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\end{array}\)

   例如：三角形三邊長為 \(3,4,5\)，求三角形面積             __。
   解法：
   (1) 因為 \(3^2+4^2=5^2\)，得直角三角形，因此，面積為 \(\frac{1}{2}\times 3\times 4=6\)。
   (2) 利用海龍公式，令 \(a = 3,b = 4,c = 5,s = \frac{{a + b + c}}{2} = 6\)，
   則 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}= \sqrt {6 \times 3 \times 2 \times 1}= 6\)。
   (3) 利用三斜求積術，令 \(a = 3,b = 4,c = 5\)，
   則 \(\begin{array}{ll}a\Delta ABC &= \sqrt {\frac{1}{4}\left[ {{a^2} \cdot {c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\\&=\sqrt {\frac{1}{4}\left[ {{3^2} \times {5^2} – {{(\frac{{{5^2} + {3^2} – {4^2}}}{2})}^2}} \right]}\\&=\sqrt {\frac{1}{4}(9 \times 25 – 9 \times 9)}\\&=\sqrt {\frac{1}{4} \times 9 \times 16}= 6\end{array}\)

總之，海龍公式與三斜求積術雖然形式看起來相異，但是，其本質是相同的，也可以說是等價的數學證明，有興趣的讀者何妨試試看！

連結：數學之旅：三角形面積公式(III)