費米-狄拉克分布

Posted on 2015/02/06 in 熱, 物理, 統計熱物理學 Statistical Thermodynamics with 沒有迴響 21,932 views

費米-狄拉克分布 (Fermi-Dirac distribution)
國立臺灣大學物理學系 100級郭宇安

「自旋」(spin)是許多粒子都具有的基本性質。科學家將自旋為整數倍的粒子稱為「玻色子」(boson)，比如光子；將自旋為半整數倍的粒子稱為「費米子」(fermion)，比如電子。對於玻色子而言，同一量子態可以佔據無數的粒子，然而對於費米子而言，同一量子態僅能容納一顆粒子──這使得兩者在統計上出現差別，以下僅就由費米子所衍生出的「費米－狄拉克分布」(Fermi-Dirac distribution)做討論。

圖一$$~~~$$（圖片來源：作者繪製）

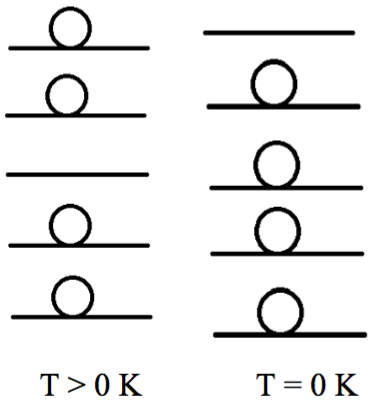
圖一中，每一條橫線為不同的能階。表示在特定溫度下，可能產生的粒子分布，不難看出：若溫度不為絕對零度，則有些量子態可能產生空缺，即沒有任何粒子恰巧具有符合的量子態；而在溫度為絕對零度時，粒子會從能量最低的量子態開始「佔據」直到底下所有的量子態全部填滿，而具有最高能量的量子態所處的能階即為「費米能階」(Fermi energy level)。

假設在總能為 $$E$$ 的情況下，某一個特定能階 $$\epsilon_j$$ 有 $$d_j$$ 種不同量子簡併態，且在該能階有 $$N_j$$ 個粒子，則如此共有 $$C_{N_j}^{d_j}$$ 種排列可能性，

若總共有 $$N$$ 個粒子，則剩下 $$N-N_j$$ 個粒子可以在其他能階中排列。因此，由最低的能階開始填入費米子，總共有$$Q(N_1,N_2,N_3,…)$$種方法，其中

$$Q(N_1,N_2,N_3,…)=\prod_{j=1}^{\infty} C_{N_j}^{d_j}=\prod_{j=1}^{\infty}\frac{d_j!}{N_j!(d_n-N_n)!}$$

在引入拉格朗日乘子法 (Lagrangian multiplier method)計算之後，在總能為 $$E$$、總粒子數為 $$N$$ 的情形下，某一能階 $$\epsilon_i$$ 最有可能填入的粒子數為 $$N_j$$。其中 $$\displaystyle N_j=\frac{d_j}{e^{(\epsilon_i-\mu)/kT}+1}$$ ，$$\mu$$ 為化學勢（chemical potential，或稱化學位能），$$k$$ 為波茲曼常數。

因此，平均某一量子簡併態可填入的粒子數（或說是某一量子簡併態被填入的機率）為 $$\overline{N_j}=\displaystyle\frac{1}{e^{(\epsilon_i-\mu)/kT}+1}$$。

圖二$$~~~$$圖中 $$\mu=5eV$$（圖片來源：http://www.doitpoms.ac.uk/tlplib/semiconductors/fermi.php）

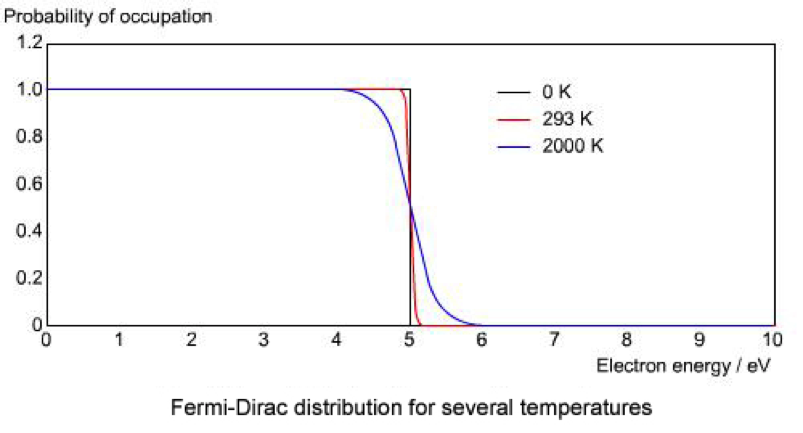
由圖二可以看出，當溫度為絕對零度時，是不會有能量大於 $$5$$ 電子伏特的例子出現，所有粒子都將填入能量低於5電子伏特能階的量子態；而當溫度上升時，漸漸有粒子可以獲得比化學位能還高的能量，進而填入能量大於 $$5~eV$$ 的量子態，因此曲線在 $$5$$ 電子伏特該點的斜率有減緩的現象。

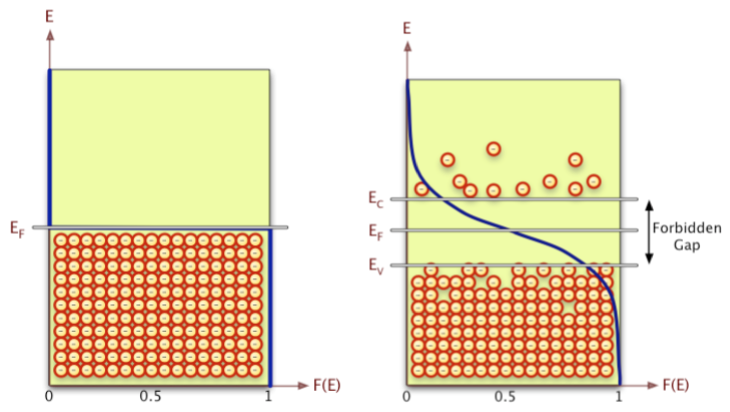
由於金屬以及半導體是靠電子導電，而電子必須滿足費米-狄拉克分布，所以我們可以利用上述費米-狄拉克分布的特性去解釋這類物質的導電特性。例如圖三為半導體的能帶，在溫度為絕對零度時，電子僅能從最低一路填到最高的費米能階 $$E_F$$，因而無法到達傳導帶（最低能量為 $$E_C$$ 的能帶），進行傳導；由能帶理論可以推論：在能帶間隙中是沒有電子位於該能階上的。因此溫度必須要到達一定程度，才能讓底下的能階的電子躍遷到傳導帶進行傳導。