哈利波特的魔法透鏡

哈利波特的魔法透鏡 (Harry Potter’s magical lens)
國立臺灣大學物理系教授 陳義裕

雖然哈利波特的隱形斗蓬令人欣羨，但是小說家的想像力常常是領先科學家一截，所以如果我告訴你科學家直到今天仍然無法在隱形斗蓬的研究上取得令人滿意的進展，我猜你可能也不會很失望。但是，沒有突破性進展是一回事，這可不代表就沒有人想得出妙點子來！於 2014 年，Rochester 大學的光學家 Howell 教授和他的研究生 Choi 利用簡單的透鏡組合，示範了如何以非常低成本在自家完成（一如你我的）窮苦人家的隱身夢想！

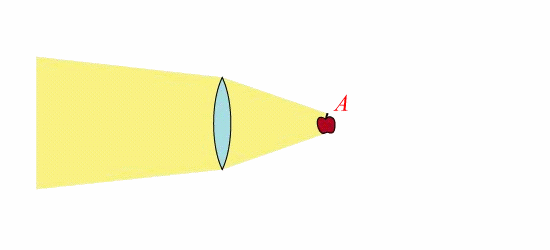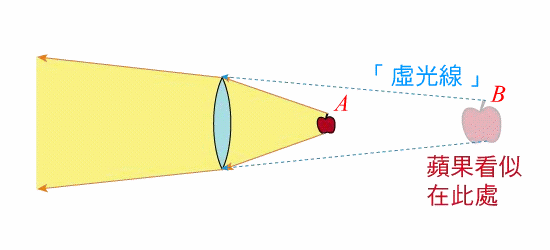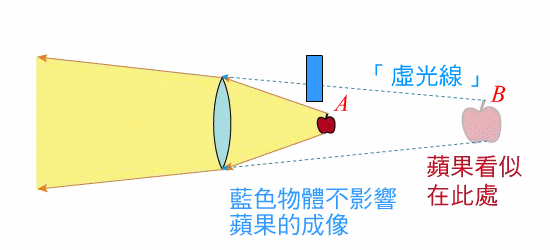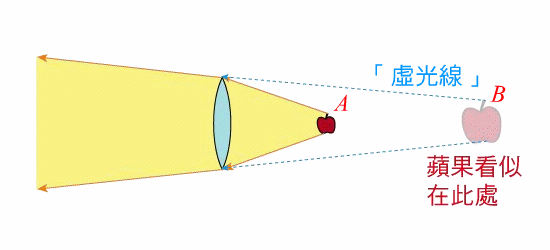
在介紹他們的發明之前，我們先把此中最重要的概念點出來：圖一中的蘋果 $$A$$ 所發射出的光線會經由凸透鏡折射而形成一個虛像，此虛像的光線似乎是從 $$B$$ 處所發出。此時若將另一個（藍色）物體插入圖一中，使它看似擋住了來自 $$B$$ 的「虛光線」，但實際上完全沒有碰觸到真實光線所行經的位置（米黃色區域），則人們自然無法經由透鏡去看到插入的物體（因為只會看到虛像），於是隱形斗篷就奏效了。把這個想法修改一下，你可以直接利用身邊的物品去做個隱形斗篷、變個小魔術！（請下載觀看示範影片 Cloaking Demo-Compressed.avi；檔案稍大，有7MB）

圖一

當然，上述想法其實並未真正達到隱身的要求，原因是我們透過透鏡所看到的虛像要嘛就是被放大了、要嘛則是左右或上下顛倒了，所以看到虛像的人立刻會警覺到必然有人在中間做了手腳。

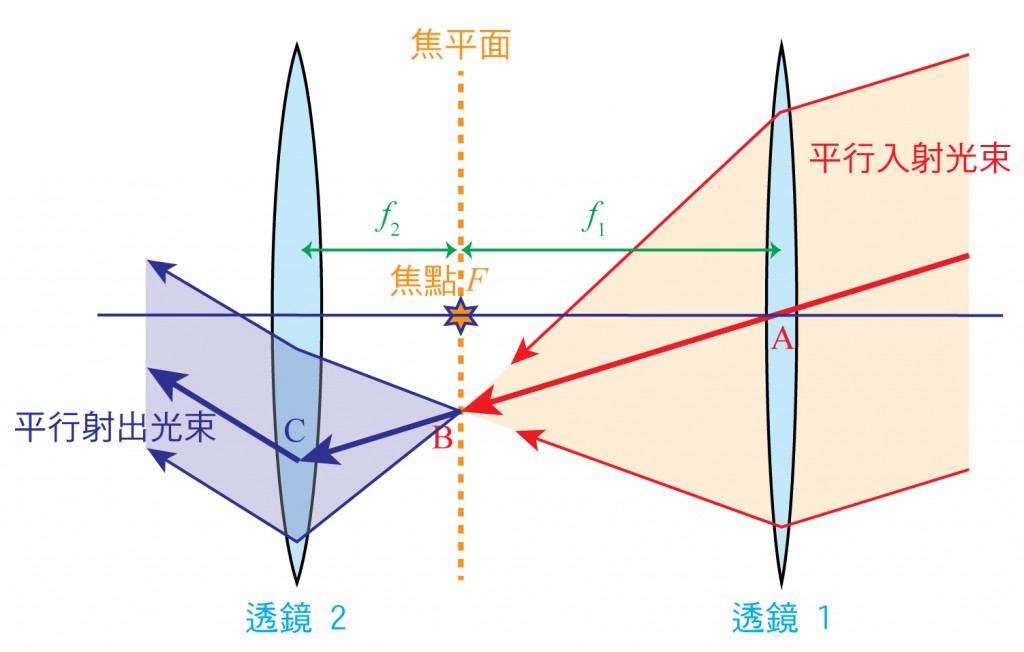
那要如何改進呢？在繼續討論之前，先做一點暖身操。在中學的物理課中我們都學過：一束平行光進入薄的凸透鏡後會在透鏡的焦平面上聚焦成像（圖 2，光束自右邊射入，聚焦在 $$B$$ 點）。此外，通過透鏡中心的任何光線（例如圖中的 $$AB$$）都不會被透鏡所偏折。所以，如果我們把焦距分別是 $$f_1$$ 以及 $$f_2$$ 的兩個薄透鏡平行擺放在一起，使它們之間的距離為 $$f_1+f_2$$（所以它們有共同的焦點和焦平面），接著以一束平行光斜向自透鏡 1 入射，則從透鏡 2 射出來的光線仍然會是平行光，只是它傾斜的角度改變了：除了角度的數值不同之外，你也會注意到原來往下方射入的光束現在卻變成往上方射出（圖2）。

圖二

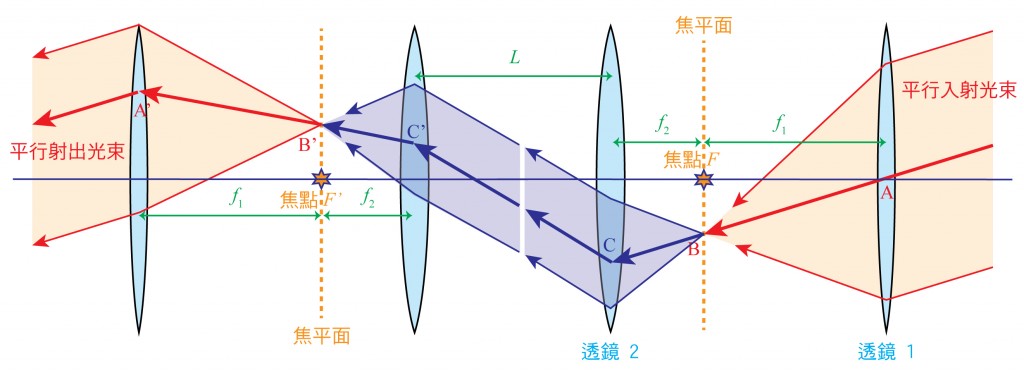
可以想見的，如果我們取來兩套相同的這種雙透鏡組，讓它們反向面對，然後重新做實驗，從第一個透鏡組射入一道平行光束，接著再讓射出來的光束通過第二個透鏡組，則最後射出來的不但仍然是平行光，而且這一回角度完全沒有改變。不僅如此，我們還可注意到：這個結果和兩組透鏡間的距離 $$L$$ 也完全無關（圖3）。

圖三

這麼大費周章，最後射出來的光線連傾斜角度都沒有改變、似乎只做了虛功，其目的何在？原來關鍵在透鏡組間的距離 $$L$$！從圖 3 中你一定注意到了：雖然調整 $$L$$ 完全不會改變射出光線的角度，但是卻會影響標示為粗線的那道光線在透鏡上的高低位置。

更明確地說，$$L$$ 越長，則 $$C’$$ 的位置越高，於是 $$A’$$ 的位置就越低。如果我們適當地調整 $$L$$ 值，使得 $$A’$$ 的位置剛好落在 $$ABC$$ 的延長線上，則對於透鏡組左方的觀察者來說，這整個透鏡組似乎沒有對原始光線動到任何手腳！可是我們明明知道，這光線在透鏡之間傳播時其實曾經被聚集在一起過(例如在兩個焦平面附近，光線其實是收攏在一起的)，因此，將一個物體插入這些區域，但牢記不要去遮蔽到真實光線的軌跡，則物體對觀察者來說就被遮掩住，於是隱形斗蓬的效果就發揮出來了。經過簡單的計算可以發現(參見附錄)，這個適當的 $$L$$ 值為：

$$\displaystyle L=2f_2\frac{(f_1+f_2)}{f_1-f_2}$$

雖然這個隱身術看起來很低科技，但是想一想，能夠從最簡單的物理現象中發掘出別人硬是沒有料到的奇招，這其實也是科學研究的樂趣所在。更何況，這樣一個隱身術不純粹只是具有娛樂效果而已。根據 Howell 教授的說法，未來我們說不定可以利用這種想法去發明出一種不會被手以及器械擋住視線的手術專用觀視鏡哩（換言之，手以及器械都被隱身了）！

附錄：（魔法透鏡的簡單數學推導）

兩組透鏡間的距離 $$L$$ 要取什麼數值才可以達到隱形的目標呢？以下利用簡單的幾何學進行推導。

圖四

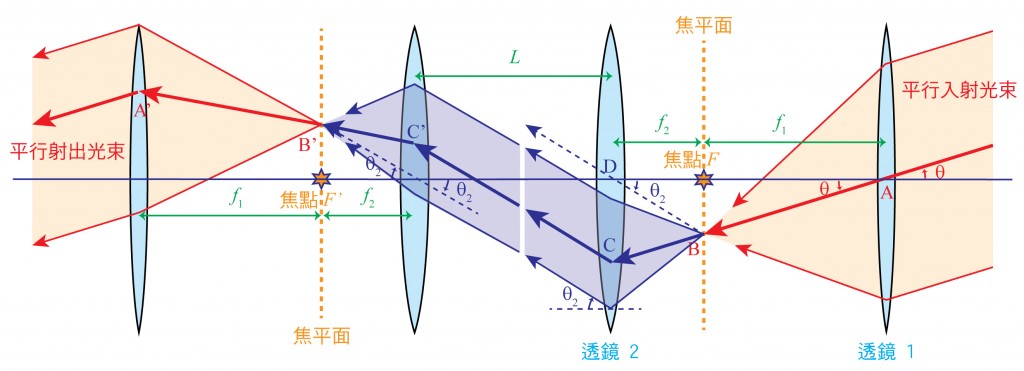
假設入射光線的傾斜角度 $$\theta$$ 並不大，則從透鏡2射出來的光線之傾斜角度 $$\theta_2$$ 可以透過下式來求得（參見圖4中的三角形 $$AFB$$ 及 $$DFB$$）：

$$\begin{array}{l}\overline{FA}\cdot \theta=\overline{FB}=\overline{FD}\cdot \theta_2\\ \Rightarrow f_1\theta=\overline{FB}=f_2\theta_2\Rightarrow \theta_2=\frac{f_1}{f_2}\theta\end{array}~~~~~~~~~(1)$$

此外，$$\overline{DC}=(f_1+f_2)\theta$$

亦即 $$C$$ 點的縱座標為 $$y_c=-(f_1+f_2)\theta$$。(負號是因為它在橫軸下方)
進一步，可以看出 $$C’$$ 點的縱座標為

$$y_{C’}=L\theta_2-\overline{CD}=L\frac{f_1}{f_2}\theta-(f_1+f_2)\theta~~~~~~~~~(2)$$式

若將 $$C’B’$$ 的傾斜角記成 $$\theta_3$$(圖4並未示出)，則

$$\theta_3=\frac{\overline{B’F’}-y_{C’}}{f_2}=\frac{f_2\theta_2-y_{C’}}{f_2}~~~~~~~~~(3)$$式

所以 $$A’$$ 點的縱座標為  $$y_{A’}=y_{C’}+(f_1+f_2)\theta_3~~~~~~~~~(4)$$式

把 $$(3)$$式、$$(2)$$式、和 $$(1)$$式的結果代入 $$(4)$$式，整理之後可得：

$$y_{A’}=\theta\frac{f_1}{f_2}[2(f_1+f_2)-\frac{f_1}{f_2}L]~~~~~~~~~(5)$$式

如果我們要求 $$A’$$ 點剛好落在 $$ABC$$ 的延長線上，則必定

$$y_{A’}=-\theta\{(f_1+f_2)+L+(f_1+f_2)\}~~~~~~~~~(6)$$式

令 $$(5)$$式 和 $$(6)$$式 相等，於是便可推導出

$$\displaystyle L=2f_2\frac{f_1+f_2}{f_1-f_2}$$

當然，你也可以利用中學物理學過的物距以及像距的公式

$$(1/$$物距$$)+(1/$$像距$$)=1/$$焦距

來推導出以上的結果。限於篇幅，我們就不在此贅述。

參考文獻

1. ‘Cloaking’ device uses ordinary lenses to hide objects across range of angles. — University of Rochester.
   http://www.rochester.edu/newscenter/watch-rochester-cloak-uses-ordinary-lenses-to-hide-objects-across-continuous-range-of-angles-70592/