算幾不等式的應用(1)

算幾不等式的應用(1)
國立臺南第一高級中學數學科教師 林倉億

本網站的文章中，屏東高中楊瓊茹老師的〈算幾不等式〉與蘭陽女中陳敏晧老師的〈算幾不等式的證明(Ⅰ)〉、〈算幾不等式的證明(Ⅱ)〉已詳細說明了何謂算幾不等式，並給出了多種證明。本文將舉幾例說明算幾不等式在高中數學中的應用，並提醒讀者在應用算幾不等式時常犯的錯誤。

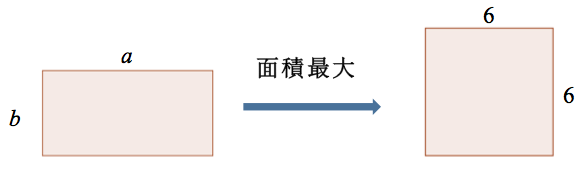
在高中數學中的算幾不等式最主要用於求最大、最小值。比如說，翰林版課本《普通高級中學數學1》中給的例子就是「使用一條 \(24\) 公分長的繩子圍一長方形，試求所有長方形中面積最大的長方形面積為何？並求此長方形的長、寬。」

此題只要假設長、寬分別為 \(a\)、\(b\)，得 \(a+b=12\)，再利用算幾不等式 \(6=\frac{a+b}{2}\le \sqrt{ab}\)，就可輕易求得面積的最大值為 \(36\)，且此時的長方形恰為邊長為 \(6\) 的正方形（參閱圖一）。

圖一（本文作者林倉億繪）

這類求幾何量的最大、最小值的應用，在高中數學科能力競賽中也經常出現。例如98學年度台灣省第一區的數學科能力競賽筆試（一）的題目中就有

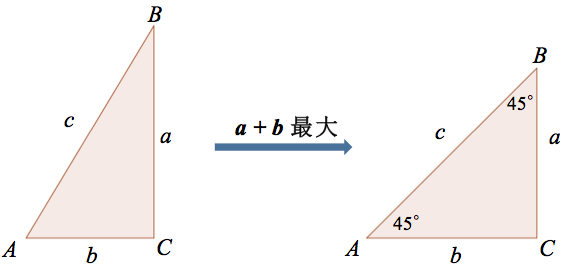
「在直角三角形 \(ABC\) 中，\(\angle C=90^\circ\)，\(\overline{AB}=c,\overline{BC}=a,\overline{CA}=b\)。
試證：\((1)c<a+b\le \sqrt{2}c\)；\((2)a+b=\sqrt{2}c\) 的充要條件為 \(a=b\)。」

此題只需要利用畢氏定理 \(c^2=a^2+b^2\)，再加上算幾不等式 \(a^2+b^2\ge 2\sqrt{a^2b^2}=2ab\)，

就可以得到 \((a+b)^2=a^2+b^2+2ab=c^2+2ab\le c^2+c^2=2c^2\)，

即 \(a+b\le \sqrt{2}c\)，同時也得知當 \(a+b=\sqrt{2}c\) 的充要條件就是三角形 \(ABC\) 為等腰直角三角形（參閱圖二）。

圖二（本文作者林倉億繪）

類似的例子亦可見於101學年度台灣省花蓮區的數學科能力競賽筆試（二）：

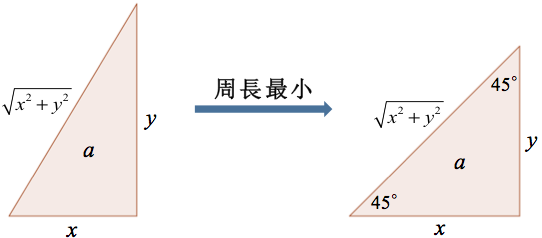
「已知直角三角形面積為 \(a\)，則其周長的最小值為________。」

我們可假設兩股為 \(x,y\)，斜邊為 \(\sqrt{x^2+y^2}\)，則 \(\frac{1}{2}xy=a\Rightarrow xy=2a\)，

再由算幾不等式可得

\(x+y\ge 2\sqrt{xy}=2\sqrt{2}\sqrt{a}\) 與 \(\sqrt{x^2+y^2}\ge \sqrt{2\sqrt{x^2y^2}}=\sqrt{2xy}=\sqrt{2}\sqrt{a}\)，

這兩者等號成立的充要條件都是 \(x=y\)，

因此，我們可以知道周長 \(x+y+\sqrt{x^2+y^2}\) 的最小值就是 \((2\sqrt{2}+2)\sqrt{a}\)，

也就是發生在等腰直角三角形的時候（參閱圖三）。

圖三（本文作者林倉億繪）

上述三個例子，都是利用算幾不等式，求出在特定條件之下，某個幾何量的最大或最小值，也就是算幾不等式在幾何中的應用。同時算幾不等式等號成立的條件，可幫助我們認識在最大或最小值發生時，該幾何圖形會有何特殊性質。特別值得注意的是，最大或最小值發生時的充要條件是算幾不等式的等號成立時；換句話說，當等號不成立時，所得之值就不會是最大或最小值了。

關於最大或最小值的說明，請先看一個簡單的例子：若 \(x\le 2\)，那顯然 \(2\) 就是 \(x\) 的最大值。不過，要是 \(x<2\)，那 \(x\) 的最大值還會是 \(2\) 嗎？既然 \(2\) 不會是 \(x\) 的值，那麼當然也就不會是 \(x\) 的最大值！事實上，在 \(x<2\) 的條件下，\(x\) 並沒有最大值，我們只能稱呼 \(2\) 是的上界中最小的上界，簡稱為「最小上界 (the least upper bound or supremum)」。

因此，等號成立與否，對最大、最小值有決定性的影響。下面這個例子筆者先提供常見的錯誤解法，讀者不妨先找找碴，再看正確的解法。解法中用到海龍公式，不熟悉此公式的讀者，可先參閱本網站蘭陽女中陳敏晧老師所寫之〈數學之旅：三角形面積公式(Ⅱ)〉。

周長為 \(24\) 的三角形，面積最大值為何？

【錯誤解法】：

設三邊長為 \(a,b,c,\displaystyle s=\frac{a+b+c}{2}=12\)，

由海龍公式知三角形面積\(=\sqrt{s(s-a)(s-b)(s-c)}\)，

利用算幾不等式可得\(\displaystyle \frac{s+(s-a)+(s-b)+(s-c)}{4}\ge \sqrt[4]{s(s-a)(s-b)(s-c)}\)，

左式\(=\displaystyle\frac{4s-(a+b+c)}{4}=6\)，

故三角形面積\(\sqrt{s(s-a)(s-b)(s-c)}\le 6^2=36\)，故最大值為 \(36\)。

【正確解法】：

設三邊長為 \(a,b,c,\displaystyle s=\frac{a+b+c}{2}=12\)，

由海龍公式知三角形面積\(=\sqrt{s(s-a)(s-b)(s-c)}\)，

利用算幾不等式可得\(\displaystyle \frac{(s-a)+(s-b)+(s-c)}{3}\ge \sqrt[3]{(s-a)(s-b)(s-c)}\)，

左式\(=\displaystyle\frac{3s-(a+b+c)}{3}=4\)，

故 \((s-a)(s-b)(s-c)\le 4^3\\\Rightarrow \sqrt{s(s-a)(s-b)(s-c)}\le \sqrt{4^3s}=\sqrt{4^3\cdot 12}=16\sqrt{3}\)

等號成立的充要條件為 \(a=b=c\)，即當三角形為正三角形時，面積有最大值 \(16\sqrt{3}\)。

兩相比較之下，讀者應不難發現「錯誤解法」中的等號是不可能成立的，也就是 \(s,s-a,s-b,s-c\) 是不可能相等的（除非 \(a=b=c=0\)，但這與 \(a,b,c\) 是邊長的假設矛盾）。

連結： 算幾不等式的應用(2)

參考文獻

1. 游森棚主編 (2015)。《普通高級中學數學1（乙版）》。台南市，翰林出版社。
2. 張海潮 (2014)。〈算幾不等式的虛應用〉。《數學頻道》第9期。台北市，三民書局。（網址：http://www.sanmin.com.tw/learning/science/highschool/math/%E6%95%B8%E5%AD%B8%E9%A0%BB%E9%81%93NO.9%20(2014.04).pdf）
3. 陳昭地 (1983)。〈「七十二學年度大學聯考數學試題」雜感〉，《數學傳播》第 7 卷第 3 期。台北市，中央研究院數學研究所。（網址：http://w3.math.sinica.edu.tw/math_media/d73/7330.pdf）
4. 潘政輝 (1983)。〈從一個聯考試題說起〉。《數學傳播》第 7 卷第 3 期。台北市，中央研究院數學研究所。（網址：http://w3.math.sinica.edu.tw/math_media/d73/7324.pdf）