母體變異數v.s.樣本變異數

母體變異數(\(\sigma^2\))v.s.樣本變異數(\(s^2\))
國立臺灣大學農藝學系 吳博雅

一、前言

每當收集完一筆資料後，可能會非常零亂、複雜，很難看出該筆資料的特性，那我們又如何整理這些資料呢？常常會畫圖表示資料的分布情形，也會計算其平均數 (mean)、中位數 (median)、眾數 (mode)…等來看該筆資料的中心位置，同時，還會計算全距 (range)、變異數 (variance)…等，來看該筆資料的分散程度，如此一來，資料收集者可以簡單敘述該資料的特性，讓有興趣者可以快速了解，取得所需的資訊，而這類的數據分析可統稱為敘述統計學 (Descriptive Statistics)。

今天我們要特別談論變異數，變異數在高中課本裡表示成：

\(\sigma^2=\displaystyle \sum_{i=i}^{N}\frac{(x_i-\mu)^2}{N}~~~~~~~~~(1.1)\)

其中 \(x_i\) 為各觀測值(一共 \(N\) 個觀測值，亦即族群中一共有 \(N\) 個觀測值)；\(\mu\)(讀作mu)為族群平均數，可表示成：

\(\mu=\displaystyle\frac{1}{N}(x_1+x_2+\cdots+x_N)=\frac{1}{N}\sum_{i=1}^{N}x_i~~~~~~~~~(1.2)\)

上述所提及的變異數為母體變異數，事實上還有樣本變異數，公式表示成：

\(s^2=\displaystyle\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n-1}~~~~~~~~~(1.3)\)

其中 \(x_i\) 為各觀測值(共 \(n\) 個觀測值)；\(\bar{x}\) 為樣本平均數。

\(\bar{x}=\displaystyle\frac{1}{n}(x_1+x_2+\cdots+x_n)=\frac{1}{n}\sum_{i=1}^{n}x_i~~~~~~~~~(1.4)\)

二、母體變異數v.s.樣本變異數

大家或許會很疑惑，為什麼會有母體變異數與樣本變異數呢？他們彼此間存在哪些差異呢？

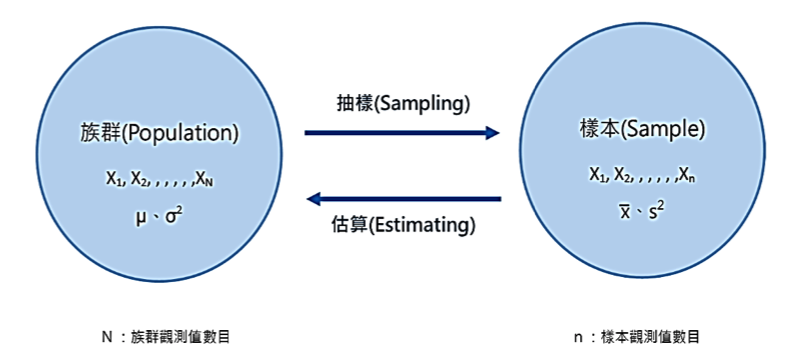
往往我們欲關注的族群資料量很大甚至是無限大，而且族群的平均數(\(\mu\))實際上常常無法知道，為了減少調查成本與增加效率，常常會藉由抽樣(sampling)取得樣本資料，希望能藉由樣本資料，獲得樣本平均數與樣本變異數，利用樣本平均數(\(\bar{x}\))來估計族群平均數(\(\mu\))，與利用樣本變異數(\(s^2\))來估計母體變異數(\(\sigma^2\))，進而了解整個族群的狀況(圖一)。至於怎樣才是好的抽樣，才能準確估計族群，請詳見其他章節，在此不加以著墨。

圖一 族群與樣本的關係(本文作者吳博雅製）

而以樣本資料求其變異數，稱之樣本變異數，又可稱為均方(mean square)，如式子1.3。

均方公式中在分子部分，我們稱之為平方和(sum of squares)，將每一個觀測值與樣本平均數之差予以平方再加總起來；均方在分母部分是 \(n-1\) 而不是 \(n\)，其原因為如果以 \(n\) 取代 \(n-1\) 會造成當以樣本變異數來估計母群體變異數時，會發生低估(underestimate)的現象^註一，而這裡的 \(n-1\) 在統計學上稱之自由度(degree of freedom) ^註二。在數理統計上可以證明以自由度作為除數所計算出來的均方，才是族群的無偏估值^註三，亦即 \(s^2\) 才是 \(\sigma^2\) 的良好估值。

• 註一：由於
  \(\begin{array}{ll}\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2&\displaystyle=\sum_{i=1}^{n}(x_i^2-2x_i\bar{x}+\bar{x}^2)=\sum_{i=1}^{n}x_i^2-n\bar{x}^2\\&=\displaystyle \sum_{i=1}^n(x_i-\mu)^2-n(\bar{x}-\mu)^2\end{array}\)
  \(\rightarrow\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2\le \sum_{i=1}^{n}(x_i-\mu)^2\)
  若以 \(\sum_{i=1}^{n}(x_i-\bar{x})^2/n\) 作為樣本的變異數，由上式可知會發生低估的現象。
• 註二：自由度是指樣本內獨立，且能夠自由變動的離均差 \((x_i-\bar{x})\) 之個數。例如：樣本中有四個觀測值，樣本平均為6，其中三個觀測值為4、8與10，最後一個觀測值一定是6*4-(4+8+10)=2。因此，當樣本大小為4(=n)時，只有3(=n-1)個離均差可以自由變動，此時自由度等於3。
• 註三：無偏估值的介紹，請詳見另篇文章。

而有時為了計算方便，我們也可以將樣本變異數的公式表示成：

\(\begin{array}{ll} s^2 &=\displaystyle \sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n-1}\\&=\displaystyle \frac{1}{n-1}\times(\sum_{i=1}^n x_{i}^2-2\sum_{i=1}^nx_i\bar{x}+n\bar{x}^2)\\&=\displaystyle \frac{1}{n-1}\times(\sum_{i=1}^nx_i^2-n\bar{x}^2)\end{array}\)

另外，母體變異數的正平方根，稱之為母體標準差(\(\sigma\))；樣本變異數的正平方根，稱之為樣本標準差(\(s\))。

例題：

A研究員想要了解某一地區20-30歲的女性之體重，但他的時間、經費有限，所以他決定在該地去隨機抽取12位20-30歲的女性，得知她們的體重55, 45, 60, 48, 43, 52, 48, 43, 50, 50, 48, 58(單位：kg)，請問這12位學生體重的樣本變異數為多少?

\(\begin{array}{ll}\bar{x} &=\displaystyle\frac{1}{n}\times\sum_{i=1}^{n}x_i\\&=\displaystyle\frac{1}{12}(55+45+60+48+43+52+48+43+50+50+48+58)\\&=50 \end{array}\)

\(\begin{array}{ll}s^2 &=\displaystyle\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n-1}=\frac{1}{12-1}(\sum_{i=1}^{12}x_i^2-12\bar{x}^2)\\&=\displaystyle\frac{1}{11}(30328-12\times 50^2)\\&=29.82 \end{array}\)

參考文獻

1. 沈明來 (2014) 生物統計學入門第六版。第三章-敘述統計學。
2. 郭寶錚、陳玉敏(2011) 生物統計學。第4章-資料集中趨勢及變異性的測度。
3. 江振東、政治大學統計系｜淺談自由度（樣本標準差公式中的分母為什麼要採用n-1）。http://mathcenter.ck.tp.edu.tw/Resources/Ctrl/ePaper/ePaperOpenFileX.ashx?autoKey=16