F分布

F分布 (F-distribution)
國立臺灣大學農藝所生物統計組碩士班 顏芷筠

• 前言

變異數同質性 (homogeneity of variance) 是許多假說檢定法需要遵守的前提假設。舉例來說，為了檢定不同品牌的燈泡的使用壽命是否有顯著的差異，我們從賣場購滿 A、B、C 三種品牌的燈泡各五顆，並實際將所有燈泡點亮、記錄燈泡壽命小時數。這個試驗有三組獨立的樣本、樣本大小各為 \(5\)，分別取自 A、B、C 三種品牌的三個母體。我們希望可以從檢定過程中，了解三個品牌燈泡壽命小時數的母體平均數之間是否有顯著差異，常用的方法為變方分析，可是此方法有前提假設如下列三項：

1. 獨立性 (independence)：觀測值來自彼此獨立的隨機樣本（例：三個燈泡品牌的樣本各自獨立）。
2. 常態性 (normality)：樣本必須隨機抽樣自服從常態分布的母體（例：三個燈泡品牌的壽命小時數服從常態分布）。
3. 變異數同質性 (homogeneity of variance)：各組樣本必須隨機抽樣自變異數相等的母體（例：三個燈泡品牌的壽命小時數的母體變異數相等）。

因此在進行母體平均數差異分析之前，必須先檢查各母體的變異數是否相同，此時就需用到 \(F\) 分布，如此可避免後續分析結論有誤。我們先介紹 \(F\) 分布進行兩母體變異數比較的假設檢定方法，再延伸至 \(F\) 分布的定義。

• 兩母體變異數比的假設檢定

假說檢定兩族群變異數 是否相同時，兩族群變異數並定是未知數（因此才需要檢定），需要利用兩樣本變異數(\(S^2_1,S^2_2\))來推論兩族群變異數是否相等（是否符合變異數同質性），若 \(S^2_1=S^2_2\) 或  \(S^2_1/S^2_2\) 比值接近 \(1\)，可以推斷 \(\sigma^2_1=\sigma^2_2\)。對應到假說檢定的步驟如下：

1. 建立虛無假說 \(H_0:\sigma^2_1=\sigma^2_2\)，兩族群變異數相同。
2. 建立對立假說 \(H_1:\sigma^2_1\ne\sigma^2_2\)，兩族群變異數不相同。
3. 定顯著水準 \(\alpha\) 值 \(=0.05\) 或 \(0.01\)。
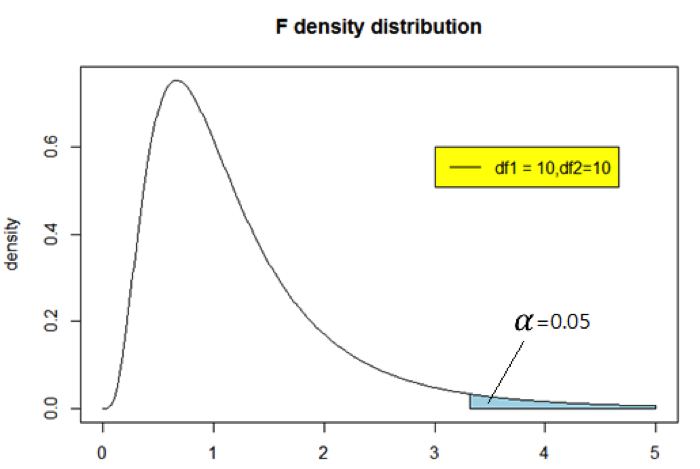
4. 假設 \(S^2_1>S^2_2\)，計算檢定統計量 \(F=S^2_1/S^2_2\)，若 \(F>F_{\alpha/2,n_1-1,n_2-1}\)，則可得結論為：拒絕虛無假說，表示兩族群變異數不相同；若 \(F<F_{\alpha/2,n_1-1,n_2-1}\) ，則可得結論為：不拒絕虛無假說，表示兩族群變異數相等。其中 \(F_{\alpha/2,n_1-1,n_2-1}\) 為 \(F\) 分布的 \(100(1-\alpha)\%\) 百分位數，亦即 \(F\) 分布由 \(F_{\alpha/2,n_1-1,n_2-1}\) 積分到無限大所得的結果為 \(\alpha\)（圖一標示的面積）。

圖一 F分布曲線圖。（本文作者顏芷筠繪）

• \(F\) 分布

\(F\) 分布與兩個卡方分布的比值有關係，若 \(U\) 隨機變數抽取自自由度為 \(r_1\) 的卡方分布，\(V\) 隨機變數抽取自自由度為 \(r_2\) 的卡方分布，且 \(U\) 與 \(V\) 互為獨立，則

\(\displaystyle\frac{U/r_1}{V/r_2}\) 為循一自由度為 \((r_1,r_2)\) 之 \(F\) 分布，記作 \(F(r_1,r_2)~~~~~~(1)\)

\(F\) 分布具有連續性、右偏性，但當兩個自由度接近無限大時，\(F\) 分布會趨近於常態分布，且 \(F\) 分布會隨著 \(\alpha\) 值及自由度之組合改變而有所不同。為了紀念首創該分布的 R. A. Fisher，故以 \(F\) 表示之。

如我們從一常態分布 \(N (\mu_1,\sigma^2_1)\) 的母體去隨機抽取 \(n_1\) 個樣本，並計算它們的樣本變異數 \(S^2_1\)，得統計值

\(\displaystyle \frac{(n_1-1)S^2_1}{\sigma^2_1}\)

服從自由度為 \((n_1-1)\) 的卡方分布。同理， \(\frac{(n_2-1)S^2_2}{\sigma^2_2}\) 服從自由度為 \((n_2-1)\) 的卡方分布，根據 \((1)\) 式的定義，

\(\displaystyle F=\frac{\frac{(n_1-1)S^2_1}{\sigma^2_1}\cdot\frac{1}{(n_1-1)}}{\frac{(n_2-1)S^2_2}{\sigma^2_2}\cdot\frac{1}{(n_2-1)}}=\frac{S^2_1}{S^2_2}\cdot\frac{\sigma^2_2}{\sigma^2_1}~~~~~~(2)\)

為循一自由度為 \((n_1-1,n_2-1)\) 之 \(F\) 分布，記作 \(F (n_1-1,n_2-1)\)。

欲檢定兩母體變異數是否相等時，\((2)\) 式在 \(H_0\)：兩族群變異數相等 \((\sigma^2_1=\sigma^2_2)\) 成立時，因為 \(\sigma^2_2/\sigma^2_1=1\)，可簡化為

\(\displaystyle F=\frac{S^2_1}{S^2_2}\sim F(n_1-1,n_2-1)\)（循一自由度為 \((n_1-1,n_2-1)\) 之 F 分布）

在計算 \(F\) 值時，常把較大的變異數置於分子，較小的變異數置於分母，因此如查詢 \(F\) 分配表，放入相對應的 \(\alpha\) 值及自由度，可發現其數值均大於 \(1\)，故此 \(F\) 值可僅與 \(F\) 分布的右尾百位數值比較。

參考文獻

1. 沈明來 (2014) 生物統計學入門。第十章-F分布與變方分析。九州圖書文物有限公司。
2. 楊惠齡, & 林明德 (2011) 生物統計學。第四章-機率分配。
3. Chih-Li Wang。第十章、兩母體之假設檢定｜銘傳應用統計系。http://www.mcu.edu.tw/department/management/stat/ch_web/etea/Statistics-3-net/chap1718.pdf。