無偏性、有效性及一致性

無偏性、有效性及一致性(Unbiasedness ,Efficiency and Consistency)
國立臺灣大學農藝學系 鍾秉元

一、前言

在統計中，推論統計是很重要的一個部分。當我們進行抽樣之後，期望以抽取出來的樣本，對母體的一些參數進行估計。點估計與區間估計是進行估計的兩種方法。當我們進行點估計時，我們會對樣本取得的數據進行統計量的計算，並且以計算出的統計量來估計母體的參數。但是這就面臨一個問題，我們應該如何知道我們所利用的統計量是否真的能夠推算出我們需要的母體參數呢？對於點估計來說，我們可以利用無偏性、有效性、一致性，三個性質作為判斷的依據。

二、無偏性

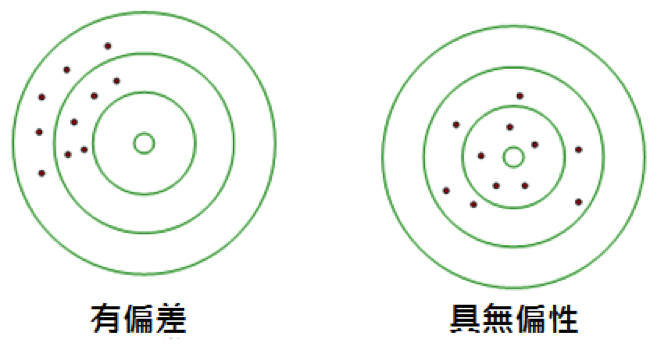
當我們在進行估計時，最重要的一點就是，我們所利用的統計值能夠準確推估出我們需要的參數，雖然每次抽樣所抽取出的樣本不同，可能會算出不同的統計量，但是這個統計量的期望值應當等於我們所要估計的母體參數。而這樣子的性質，即是無偏性 (unbiasedness) 也相當於準確度 (accuracy)。

圖一、無偏性示意圖。同心圓中心為欲估計的母體參數，紅色點為不同樣本計算所得之估計值。（本文作者鍾秉元繪製）

若我們想要估計的母體參數為 \(\theta\)，則 \(\theta\) 的無偏估計值應記為 \(\hat{\theta}\)，因此可得：

\(E(\hat{\theta})=\theta\)

即估計值之期望值會等於欲估計之母體參數。

舉例來說，如果母體的分布是常態分佈 \(N(\mu,\sigma^2)\) 。其中，母體平均為 \(\mu\)，母體變異數為 \(\sigma^2\)。在進行抽樣之後，我們可以得到在抽出 \(n\) 個樣本後，樣本的平均為 \(\overline{x}\)，以及樣本變異數為 \(S^2\)。若要進行母體平均值的估計的話，樣本平均數即為母體平均數的無偏估計值，證明如下。

\(\begin{array}{ll}E(\overline{x})&=\displaystyle E\left[\frac{1}{n}\left(\sum^n_{i=1}x_i\right)\right]&=\displaystyle\frac{1}{n} E\left(\sum^n_{i=1}x_i\right)\\&=\displaystyle \frac{1}{n}\left[\sum^n_{i=1}E(x_i)\right]&=\displaystyle\frac{1}{n}\left[\sum^n_{i=1}\mu\right]\\&=\displaystyle\frac{1}{n}(n\times \mu)&=\mu\end{array}\)

此外，用相同方法也能得知樣本變異數為母體變異數的無偏估計，證明如下。

\(\begin{array}{ll}E(S^2)&=\displaystyle E\left[\frac{1}{n-1}\sum^n_{i=1}(x_i-\overline{x})^2\right]\\&=\displaystyle\frac{1}{n-1} E\left[\sum^n_{i=1}x_i^2-2x_i\overline{x}+\overline{x}^2\right]\\&=\displaystyle \frac{1}{n-1}E\left(\sum^n_{i=1}x_i^2-n\overline{x}^2\right)\\&=\displaystyle\frac{1}{n-1}\left[\sum^n_{i=1}E(x_i^2)-nE(\overline{x}^2)\right]\\&=\displaystyle\frac{1}{n-1}\{n[Var(x_i)+E^2(x_i)]-n[Var(\overline{x})+E^2(\overline{x})]\}\\&=\displaystyle\frac{1}{n-1}\left[n\left(\sigma^2+\mu^2\right)-n\left(\frac{\sigma^2}{n}+\mu^2\right)\right]\\&=\displaystyle\frac{1}{n-1}(n\sigma^2-\sigma^2)=\sigma^2\end{array}\)

因此，藉由無偏性的證明，可以確保我們所利用的統計值能夠期望作為一個準確的估計值。

三、有效性

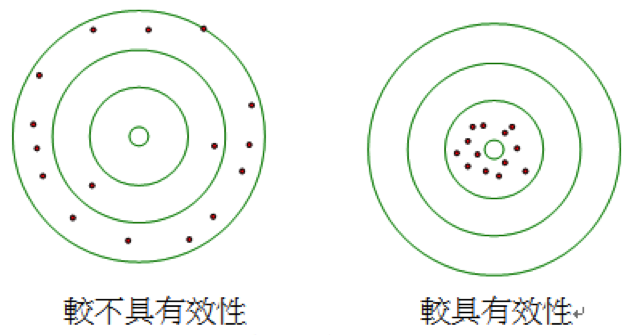
了解無偏性之後，在抽樣時，就算能夠確保估計值的期望值能夠符合所要估計之母體參數，但是每次估計時，根據抽取的樣本不同，估計出來的結果會不相同，因此我們希望每次估計時所得到的估計量都不要相差太遠，才能確保不會有相差太遠的極端值產生。也就是說估計值的變異數越小越好。變異數較小的估計值，即是較具有效性 (efficiency) 的估計值。有效性也相當於精密度 (precision)。

圖二、有效性示意圖。同心圓中心為欲估計的母體參數，紅色點為不同樣本計算所得之估計值。（本文作者鍾秉元繪製）

因此我們可以得知當 \(\theta\) 為我們欲估計之母體參數，而 \(\hat{\theta}\) 為其估計值時，\(Var(\hat{\theta})\) 越小，則該估計值越能準確表達出我們欲估計之母體參數。

四、一致性

根據大數法則，如果我們在抽樣時，抽出的樣本數越多，則估計值等於欲估計之母體參數的真值得機率會提高。而在抽出的樣本趨近無限多的情況下，估計值等於母體參數真值的機率應該要等於一，因為當樣本數趨近無限大時，可預期能夠抽出所有母體，因此估計值應當與母體參數真值相等。此性質即為一致性。

因此根據一致性的定義，當 \(\theta\) 為我們欲估計之母體參數，而 \(\hat{\theta_n}\) 為其在抽出 \(n\) 個樣本之下的估計值時，可得：

\(\displaystyle P(\lim_{n\to\infty}\hat{\theta_n}=\theta)=1\)

另一方面，在已知某個估計值為無偏估計值的情況下，當樣本數趨近無窮大時，該估計值的變異數等於 \(0\) 的話，也能說明該計值符合一致性。因為無偏性的性質說明此估計值的期望值會是母體參數，而變異數為 \(0\) 說明了沒有偏差，因此此估計值能夠等於母體參數真值。

舉例來說，樣本平均數是母體平均數的無偏估計值，而樣本平均數的變異數 \(V(\overline{x}_n)=\frac{\sigma^2}{n}\)在樣本數趨近無限大的情況下，可得：

\(\displaystyle \lim_{n\to\infty}V(\overline{x}_n)=\lim_{n\to\infty}\frac{\sigma^2}{n}=0\)

因此樣本平均數作為母體平均數的估計值，具有一致性。

五、例題

在符合常態分佈 \(N(\mu,\sigma^2)\) 的母體中抽出 \(10\) 個樣本，現在有兩個統計量用來估計母體平均數，如下

\(\displaystyle T_1=\frac{x_1+2x_{10}}{3}\)

\(\displaystyle T_2=\frac{1}{10}\sum^{10}_{i=1}x_i\)

試計算兩個統計量是否有無偏性？哪一個較具有有效性？

解：

\(\displaystyle E(T_1)=E\left(\frac{x_1+2x_{10}}{3}\right)=\frac{1}{3}[E(x_1)+2E(x_{10})]=\frac{1}{3}(\mu+2\mu)=\mu\)

\(T_1\) 具無偏性

\(\displaystyle E(T_2)=E\left(\frac{1}{10}\sum^{10}_{i=1}x_i\right)=\frac{1}{10}\sum^{10}_{i=1}E(x_i)=\frac{1}{10}(10\mu)=\mu\)

\(T_1\) 具無偏性

\(\displaystyle V(T_1)=V\left(\frac{x_1+2x_{10}}{3}\right)=\frac{1}{9}V(x_1)+\frac{4}{9}V(x_{10})=\frac{5}{9}\sigma^2\)

\(\displaystyle V(T_2)=V\left(\frac{1}{10}\sum^{10}_{i=1}x_i\right)=\frac{1}{100}\sum^{10}_{i=1}v(x_i)=\frac{1}{100}(10\sigma^2)=\frac{1}{10}\sigma^2\)

\(V(T_1)>V(T_2)\) 故 \(T_2\) 較具有效性

參考文獻

1. Probability and Statistical inference (2015), 9th edition by Hogg& Tanis & Zimmerman.
   chapter6 point estimation
2. 統計學:方法與應用 (四版)：林惠玲、陳正倉。第10章 統計估計- 點估計。