拉丁方設計介紹

拉丁方設計介紹(Introduction of Latin Square Design)
國立臺灣大學農藝學系 黃昭惠

一、原理

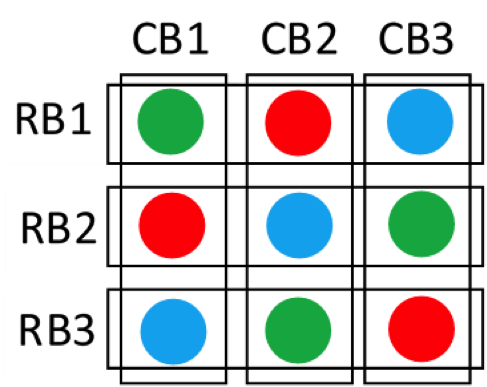
與《隨機完全區集設計介紹》一文所提及的 RCBD 隨機完全區集設計相同，拉丁方設計 (Latin Square Design, LSD) 也是一種與區集因子相關聯的設計方法，不同的是我們在中 RCBD 只有一個區集因子，稱為單向區集設計 (one-dimensional block)，而 LSD 可以同時控制兩個區集因子的影響，故屬於兩向區集設計 (two-dimensional block)，透過行區集與列區集的規劃（圖一），實驗者即可有效控制兩干擾因子的影響。

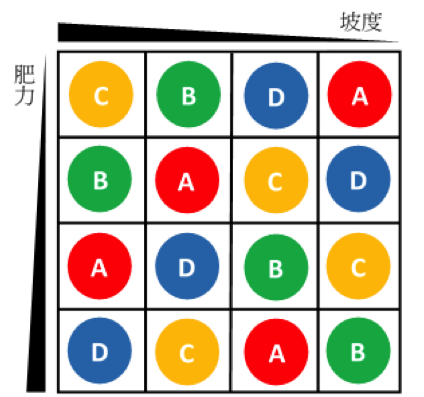
以坡地且肥力不同之牧草品種實驗為例，假設有 A、B、C、D 四種品種於坡地上進行比較試驗，每種品種四重複，其實驗目的為檢驗此四品種的牧草產量是否具有明顯的差異，已知坡度和肥力為兩個干擾因子，故我們可以使用 LSD 進行實驗的配置（圖二）。

LSD 能同時兼顧成本以及區集效應，不過在使用 LSD 進行實驗配置時，有幾個需要被遵守的規則：

1. 試驗單位須為異質性，並且能夠以兩向區集將干擾因子進行區分。
2. 參試處理數 = 行區集數 = 列區集數。
3. 參試處理在行、列區集中皆只能出現一次，並且需隨機排列於區集中。

二、分析方法

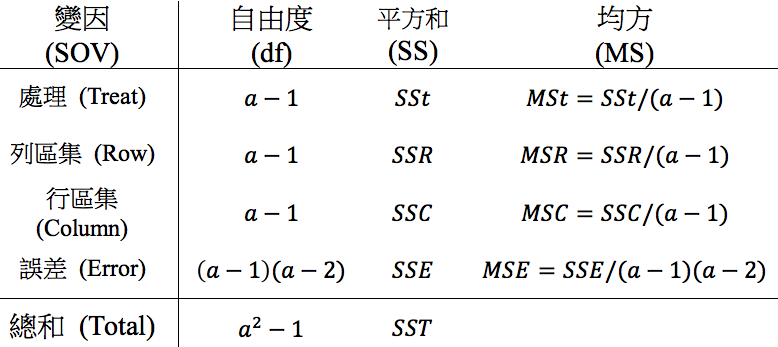
我們採用 ANOVA 變方分析表（表一）進行資料分析與判讀，

令 \(y_{ijk}\) 為第 \(j\) 區集、第 \(k\) 行集區之第 \(i\) 處理的觀測值 \((i=1,\cdots,a\)，\(j=1,\cdots,b\)，\(k=1,\cdots,a)\)，\(y_{i\cdot\cdot}\) 為第 \(i\) 處理所有觀測值的總和，\(y_{\cdot j\cdot}\) 為第 \(j\) 列區集內所有觀測值的總和，\(y_{\cdot\cdot k}\) 為第 \(k\) 行區集內所有觀測值的總和，\(y_{\cdot\cdot\cdot}\) 為所有觀測值的總和，則

\(\displaystyle SSt=\frac{1}{a}\sum^a_{i=1}y_{i\cdot\cdot}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2\)

\(\displaystyle SSR=\frac{1}{a}\sum^a_{j=1}y_{\cdot j\cdot}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2\)

\(\displaystyle SSC=\sum^a_{k=1}\sum^a_{j=1}y_{\cdot\cdot k}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2\)

\(\displaystyle SST=\sum^a_{i=1}\sum^a_{j=1}\sum^a_{k=1}y^2_{ijk}-\frac{1}{N}y^2_{\cdot\cdot\cdot}\)

\(\displaystyle SSE=SST-SSR-SSC-SSt\)

則考慮 \(F_t=\frac{MSt}{MSE}\)，若 \(F_t>F_{\alpha,a-1,(a-1)(b-1)}\)（查表），則表示拒絕 \(H_0\) 的假說，至少有一項的處理效應不為 0。

三、例題

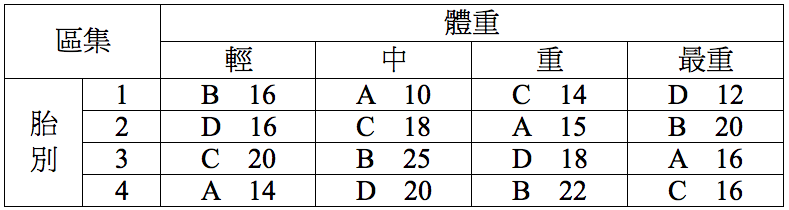
今有 A、B、C、D 四種飼料，欲檢驗不同飼料對豬隻體重輕重的影響，分別以四胎小豬，以及初始體重輕重做為行、列區集，記錄體重增加量，進行 LSD 試驗（表二），設信心水準 = 0.05。

資料分析：

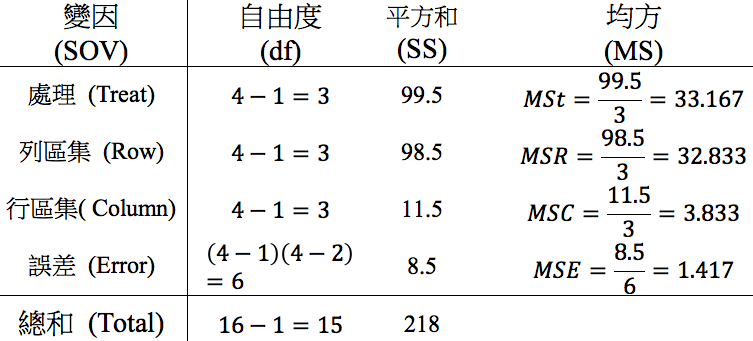
ANOVA 變方分析結果如表三。

\(\displaystyle SSt=\frac{1}{a}\sum^a_{i=1}y_{i\cdot\cdot}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2=99.5\)

\(\displaystyle SSR=\frac{1}{a}\sum^a_{j=1}y_{\cdot j\cdot}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2=98.5\)

\(\displaystyle SSC=\sum^a_{k=1}\sum^a_{j=1}y_{\cdot\cdot k}^2-\frac{1}{N}y_{\cdot\cdot\cdot}^2=11.5\)

\(\displaystyle SST=\sum^a_{i=1}\sum^a_{j=1}\sum^a_{k=1}y^2_{ijk}-\frac{1}{N}y^2_{\cdot\cdot\cdot}=218\)

\(\displaystyle SSE=SST-SSR-SSC-SSt=8.5\)

由於 \(F_t=23.4118>F_{0.05,3,6}\)，故拒絕 \(H_0\) 假說，飼料對豬隻體重具影響力。

---

參考文獻

1. 沈明來 (2012)。試驗設計學（第四版）。第八章-拉丁方設計。九州。
2. Montgomery, D. C. (2013). Design and Analysis of Experiments (eighth edition). Chapter 4.Experiments with Blocking Factors. John Wiley & Sons.