【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數

【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數
蕭維翰

連結：【物理世界】量子霍爾效應（一）：塵埃中洗滌出的整數

在前一篇筆者討論了整數的量子霍爾效應，也就是實驗中測得電導率的xy分量為電荷平方除以普朗克常數的整數倍。我們雖然沒有篇幅涵蓋實驗上所看到現象的所有必要物理概念，但至少有一個很概略的圖像：整個系統像一個公寓，公寓的樓層叫蘭道階，愈底層的公寓房租（能量）愈低，所有的電子便從第一層公寓築起，並且電子遵循庖立不相容原理（Pauli exclusion principle）所以一間房間只能住一個電子，實驗上這些整數對應到住滿的蘭道階的階數。[1]

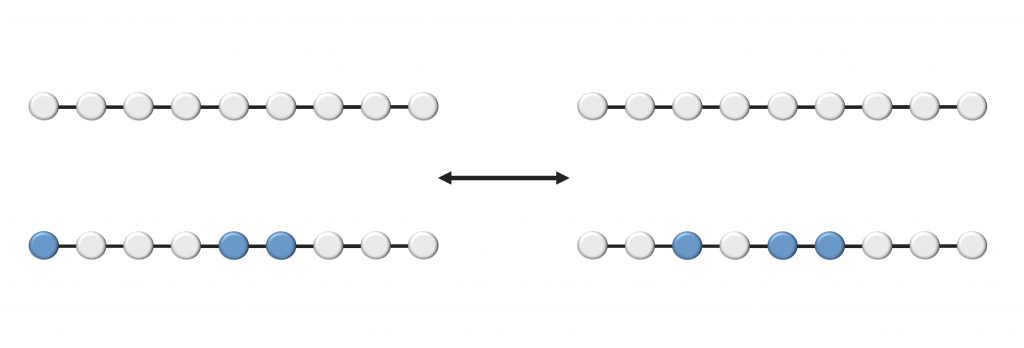
圖一：在整數霍爾效應中蘭道階的填滿狀況可以用這個卡通來示意。藍色表示有人住的房間，灰白色表示空房。即便在省略交互作用時，依舊可以想像為何電子們形成均勻流體，以及整個系統為何是個絕緣體（從所謂整個塊材的觀點）。

儘管不是很完全，但這樣的圖像已經能解釋一些現象，比如說這些電子總體看來是有均勻密度的不可壓縮流體，是一個穩定態。讀者可以想像成在住滿的蘭道階每個房間都有電子[2]，因而有均勻的密度 ; 而因為每一個蘭道階之間都有一個有限的能量差，要激發這一團電子必須克服這一個差距，也就是說某個角度而言，這個系統是一個絕緣體（insulator）。

從這個觀點看，就不難理解隔年人們發現前面的數字不一定得是整數，還可以是 \(\frac{1}{3}\) 時或其他分數時有多驚訝。拿 \(\frac{1}{3}\) 當例子，這表示第一層蘭道階只住滿了 \(\frac{1}{3}\)，那麼先驗上其實沒有理由去干涉這些電子怎麼住，今天這傢伙想住陽臺邊，明天另一個人想住家門口，沒有一個規範空間分佈的法則 ; 另外因為蘭道階不是滿的，表示當這些電子在同一個蘭道階換房間的時候，房東整體收到的房租沒有差別，與之前相比，沒有能階需要克服。

圖二：另一方面，在部分填滿的情況下，如果依舊沒有交互作用，則左右兩個狀況的總能量是一樣的，而且沒有規則去指導這些電子要怎麼分佈。

即便只有這兩件事，蘭道階都不夠用了，從理論的觀點，需要更多元素來反映或解釋，至少以下這兩點：1. 整個多體系統有均勻密度。2. 整個多體系統從最低能量到第一個激發態需要有個有限的能階差。

人們很快就想到，所謂的「蘭道問題」基本上還是一個單電子問題，我們解完單電子的蘭道階，就開始一個一個房間塞電子，而沒有考慮電子間的庫侖交互作用[3]。然而，當磁場很大所有電子都困在第一層蘭道階時，電子可視為沒有動能，這時沒有理由去忽略靜電力的影響，分數量子霍爾效應可以說是：在某些填滿的比例底下，比如說 \(\frac{1}{3},~\frac{2}{5},~\frac{3}{7}…\)，靜電交互作用規範了電子的分佈狀況，從千萬個可能的組態中選出了一個最低能量態，使它是密度均勻、不可壓縮、且具備有限的能量差。

不過物理不能止步於說說故事，在兩段之前我們提出問題，上一段發想出可能的因素，接下來就該動手做髒活，也就是做計算去看看這個點子發揮得怎麼樣了。要進行量子力學層次的物理量計算，原則上需要有這個系統的波函數，但很多個電子侷限在最低蘭道階的波函數是什麼？其實到今天都不算完全被解答。R. Laughlin 在 1982 年首先解了 2 個和 3 個電子薛丁格方程式，並在之後將結果推廣到多電子的狀況[4]。雖然這個所謂 Laughlin 波函數（Laughlin wave function）不是真正庫侖問題的解，但在數值方面獲得了極大的成功，在電腦上與真正的波函數有很大的相似，並看到能階差。除此之外，更令人驚豔的是 Laughlin 利用數學形式的類比，將利用此波函數計算的密度轉換成另外一個古典的電漿（one-component plasma ）問題，間接說明這個波函數描述的流體具有均勻的密度，還能藉此論證分數量子霍爾效應中的準粒子（quasi-particle）帶有分數電荷，比如說 \(\frac{1}{3}\) 或 \(\frac{1}{5}\) 的電子電量。

這些工作帶給了 Laughlin 1998 年的諾貝爾獎，但還不是完整的故事，譬如他無法解釋 \(\frac{2}{5}\)、\(\frac{3}{7}\) 這些分數，也留給了其他高手大鳴大放的空間。

連結：【物理世界】量子霍爾效應（三）：複合費米子

參考資料：

1. B. Laughlin, Fractional Quantization, Nobel lecture.
2. B. Laughlin, Quantized motion of three two-dimensional electrons in a strong magnetic field, Phys. Rev. B 27, 3383 (1983).
3. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations, Phys. Rev. Lett. 50, 1395 (1983).

註解：

[1] 實驗上當然不可能剛剛好「住滿」，這也就是我強調我沒有解釋所有物理的原因之一。

[2] 原則上蘭道階指的是能量上的量子化，一般而言能量的量子化跟波函數、也就是電子的空間分佈沒有絕對關係，但剛好在這個蘭道問題裡，整個材料在物理空間中被區分成很多個小房間，每個房間都有兩個號碼，一個是樓層數（蘭道階數），一個是房號（動量或角動量量子數）。

[3] 事實上我們解析原子也是這樣開始的，所以高中化學才會有一堆能量上的修正跟例外。

[4] 白話一點就是猜答案，這在物理上並不是太少見的技巧，而且通常是高手才猜得到好的答案。