密碼學的反擊

Posted on 2020/02/13 in 人工智慧, 倫理, 隱私與資訊安全 with 沒有迴響 2,803 views

密碼學的反擊
編譯／王昊謙

雖然距離商業或日常使用仍有一段距離，但量子電腦的出現威脅了現今被廣泛使用的RSA加密演算法，因此密碼學家找到了數種可能成為下一代加密方式的選擇，例如網格加密與McEliece密碼系統。

單向函數

RSA加密演算法（Rivest–Shamir–Adleman，三位創始人的姓氏）的原理是每個使用者產生一對公鑰（public key）和私鑰（private key），透過公鑰加密的訊息可以且只能透過私鑰來解密，但很難從公鑰推得私鑰。因此，若Alice要將一則訊息傳給Bob，它只需要將此訊息用Bob的公鑰加密，Bob就可以用自己的私鑰解密。竊聽者Eve即便獲得訊息，也無法只透過Bob的公鑰直接解密或推算私鑰。

公鑰與私鑰的產生方式如下：由使用者選擇兩個極大的質數\( \mathbf{p} \)和\( \mathbf{q} \)，計算兩者的積（\( N=pq \)）後，利用\( \mathbf{N} \)、\( \mathbf{p} \)、\( \mathbf{q} \)來產生公鑰和私鑰。其中\( \mathbf{N} \)伴隨公鑰發布（加密過程需要用到），\( \mathbf{p} \)和\( \mathbf{q} \)則在公鑰和私鑰產生後銷毀。理論上，Eve若可以將\( \mathbf{N} \)質因數分解成\( \mathbf{p} \)和\( \mathbf{q} \)，就可以從公鑰回推私鑰；但實際上之所以很難達成，是因為目前並沒有一個可以在有限時間內完成大數質因數分解的演算法，因此只要\( \mathbf{N} \)夠大，RSA加密是幾乎不可能被破解的。

利用某些難以反向計算的函數（例如難以從公鑰回推私鑰），我們得以利用「陷門單向函數」（trapdoor one-way function）達到加密的目的。然而一些傳統的加密演算法因為量子電腦的出現而變得不再可靠，例如麻省理工學院數學家Peter Shor於1994年所提出的演算法便可在量子電腦上破解RSA加密。密碼學家於是開始尋找後量子時代的替代方案，以下簡單介紹其中兩個候選選項──網格加密（lattice-cryptography）與錯誤校正碼（error correcting code）。

網格加密

格加密是利用連量子電腦都無法有效解決的網格問題（Lattice problem）。所謂網格，是由一組互相獨立的向量（稱為「基底」，basis），透過整數倍的線性組合所張開的空間。例如下圖中每個綠色格點都可以基底向量整數倍的線性組合表示。同一網格的基底並不唯一，如下圖的網格可以以\( \vec{b_1} \)與\( \vec{b_2} \)為基底，也可以是\( \vec{b’_1} \)與 \( \vec{b’_2} \)，然而某些基底向量（如左圖，可作為私鑰）比較容易推算出網格點的位置，例如左圖原點O到橘色箭頭處的向量，我們可以很直覺地看出是1倍\( \vec{b_1} \)與1倍\( \vec{b_2} \)的和；但對於其他基底而言（如右圖幾乎相互平行，可作為公鑰），這項任務便沒有那麼簡單了！尤其在實際運用時，網格空間動輒500個維度以上。

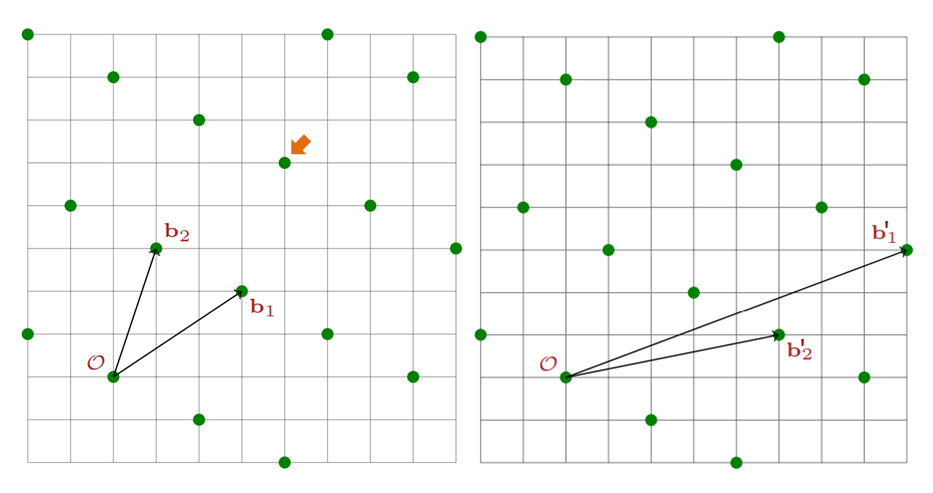
（圖片來源：改自C. Peikert, 2019.）

當Alice要傳送訊息時，先將訊息轉換成位元串（bit string），接著以向量代表每個位元，若與最靠近的格子點的幾何距離小於與周圍格子點中間的幾何距離，則代表0；反之，若該向量不靠近任何一個格子點，位於周圍格子點的中間，則代表1。Alice根據Bob的公鑰，利用這種方法將訊息加密成一系列的的座標，並傳送給Bob。Bob可以透過自己較單純的基底向量來解密，但Eve即便有量子電腦，也難以透過複雜的公鑰來解密。

McEliece密碼系統

另一種後量子加密方式則是錯誤校正碼，例如McEliece加密系統。錯誤校正碼是在欲傳遞的訊息上附加的多餘訊息，原本是用來避免原始訊息因意外導致部份的0變成1，或1變成0而導致傳遞錯誤，常見的方法有漢明碼（Hamming code）等。

其中，若錯誤校正碼的產生方式是透過一個線性變換（\( \vec{x} \mapsto \mathbf{G}\vec{x} \)），我們稱之為線性的錯誤校正碼。其中，\( \vec{x} \)是訊息，可以寫成一個向量，而矩陣\( \mathbf{G} \)則稱為這個錯誤校正碼的生成器（generator）。當然，\( \mathbf{G} \)必須滿足一些條件才能在解密時獲得唯一且正確的訊息。

在1970年代，密碼學家證明這類的方法同時具有加密的功能。McEliece加密系統就是一種利用錯誤校正碼的特性來加密的系統。Bob首先先生成一個最多允許\( \mathbf{k} \)個錯誤的校正碼生成器\( \mathbf{G} \)、一個存在反矩陣的隨機矩陣\( \mathbf{S} \)以及一個隨機的置換矩陣（permutation matrix）\( \mathbf{P} \)。接著，它計算\( \hat{\mathbf{G}} = \mathbf{SGP} \)，並將\( \left( \hat{\mathbf{G}} , t \right) \)公佈作為公鑰，\( (\mathbf{S}, \mathbf{G}, \mathbf{P}) \)則作為私鑰。Alice加密訊息\( \vec{m} \)時，則計算\( \vec{c}’ = \hat{\mathbf{G}} \vec{m} \)，並隨機選擇\( \mathbf{k} \)個\( \vec{c}’ \)的位元改變其值，最後發送訊息。如此Bob收到訊息時，可以透過\( \mathbf{P}^{-1} \)\( \mathbf{S}^{-1} \)以及原本校正解密法回推原始的訊息。Eve則因為公鑰\( \hat{\mathbf{G}} \)經過兩個隨機矩陣\( \mathbf{S} \)、\( \mathbf{P} \)打亂而難以回推私鑰\( \mathbf{G} \)，也就難以推算\( \mathbf{G} \)所對應的解密方式而獲得原始訊息。

展望

大多數的後量子加密演算法都是使用更長的金鑰，或者尋找比現今演算法所需的計算量還多的演算法，來防止量子電腦的破解。然而，荷蘭拉德堡德大學的密碼學家Simona Samardjiska與他的團隊則正在發展基於二次方程組而不需要更長的金鑰的演算法，未來或可應用於網頁的電子簽證。

然而，目前並沒有人證明以上的方法對於量子電腦是完全無法破解，甚至對於傳統電腦也是（例如若有人能提出新的、更有效率的演算法，就有可能破解相關的加密方式）。因此，微軟的密碼學家Brian LaMacchia認為：目前發展的後量子演算法應會暫時與現今的演算法同時使用，而非完全取代。美國國家標準技術研究所（National Institute of Standards and Technology，NIST）最快可能在2022年時公佈二到三種標準的加密演算法以及數位簽證。NIST的數學家Sustim Moody表示，若有人成功地破解某種加密系統，我們仍有其他演算法可供使用。LaMacchia則表示，過去30年來，密碼學歷經四到五次的重大變革，「然而這次在性質上完全不同，且複雜的多。」

編譯來源

A. Cho, “Cryptographers scramble to protect the internet from attackers armed with quantum computers“, Science, 2019.

參考資料