點到直線的距離

平面上點到直線距離（三） (The distance from a point to a line in the plane Ⅲ）
臺北市立和平高中教師黃俊瑋

連結：平面上點到直線距離（二）

本文承〈平面上點到直線距離(一)〉與〈平面上點到直線距離(二)，繼續提出三類平面上點到直線距離的解法以及相關討論與連結。而本文中的各類解法，主要在直線上任取一點或兩點，造出新向量，所延伸出的方法。

方法5：在直線上任取一點，再利用平行與垂直性質

本類方法主要是引入直線上的一點後，充份利用直線的法向量與方向向量，輔以平行與垂直相關性質與關係，求得投影點與距離。

方法5-1：在直線上任取一點，再利用平行與垂直相關性質

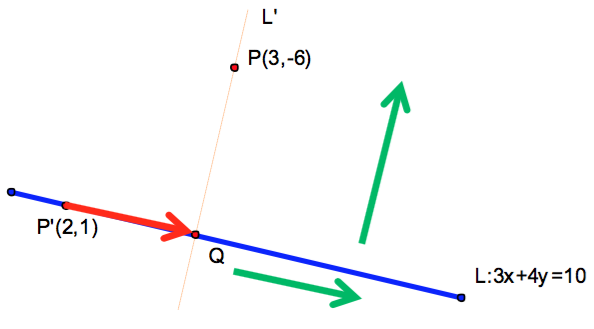
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\) ，
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點，\(\vec{P’Q}\) 與直線之方向向量平行，可設為 \(\vec{P’Q}=t(4,-3)\)。

接下來，可發展出兩種方法，分別利用直線的法向量或方向向量，搭配平行與垂直關係進行解題：

5-1-1

則 \(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 平行直線 \(L:3x+4y=10\) 的法向量
分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\)，可得 \(4(1-4t)=3(-7+3t)\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

5-1-2

\(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 垂直直線 \(L:3x+4y=10\) 的方向向量
內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求(參考圖一所示)。

圖一 在直線上任取一點，再利用平行與垂直性質(一)