導帶

導帶 (Conduction Band)
國立臺灣大學化學系 葉德緯

我們對於金屬材料的認識，最廣為人知的模型就是金屬原子間由金屬鍵 (metallic bond) 所形成的電子海 (electron sea) 模型了。電子海模型對金屬材料的導電性有不錯的解釋，不過若要對於金屬材料內部的電子能量分佈有更多的描寫，以及對於非導體材料例如半導體、絕緣體等有更好的解釋，通常都會引入能帶理論 (band theory)。

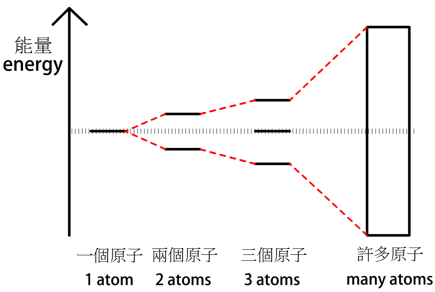
當兩個原子靠近產生交互作用而結合成分子時，他們各自的原子軌域也會交互作用形成分子軌域 (molecular orbital)，如圖一，縱軸為能量，而每條黑色橫線代表軌域，橫線所在位置對到縱軸即該軌域的能階 (energy level)。而當越多的原子結合成分子的時候，參與混成的軌域越多，產生的分子軌域也會越多，而分子軌域的能階分佈也會從一開始的不連續，逐漸形成一個近似連續的能帶 (band)。

圖一、分子軌域與能帶示意圖。（本文作者葉德緯繪）

一般來說，晶體的能帶可以分為價帶 (valence band) 以及導帶 (conduction band)，若兩個能帶沒有重疊，價帶的最高能階跟導帶的最低能階的能量差稱為能隙 (energy gap)，能隙的大小會依據不同的元素以及鍵結方式而異，金屬性越大的元素所形成的晶體，能隙會越小，甚至沒有能隙存在。相對於低能量的價帶，導帶具有較高能量，使得導帶中的電子可以脫離單一原子的束縛，成為非定域電子 (delocalized electron)。這些非定域電子具有導電性質，我們可以想像它們能夠穿梭於原子晶體之間，作為電荷載子 (charge carrier) 而傳遞電流。

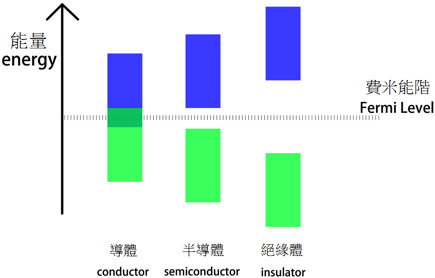
費米能階 (Fermi level) 是金屬在絕對零度 (absolute zero) 時，電子依據遞建原理 (aufbau principle) 從低能量的能階往上填滿，所能填到的最高能階。而在非絕對零度時，電子會因為熱的緣故，而有機會出現在更高的能階裡，這時費米能階會對應到電子遵守費米-狄拉克分佈 (Fermi-Dirac distribution) 時，分佈機率為 50% 的區域。對於金屬而言，導帶和價帶之間有重疊（如圖二，縱軸為能量，上方藍色為導帶，下方綠色為價帶，虛線為費米能階），而費米能階落在導帶內部，也就是導帶此時是部分填有電子的情況，因此金屬具有導電性。

圖二、導體、半導體、絕緣體的能帶分佈。（本文作者葉德緯繪）

而對於半導體以及絕緣體而言，導帶與價帶之間沒有重疊，兩者之間有能隙，而費米能階此時可以延伸其定義，以能隙中點作為費米能階，這時費米能階沒有對應到真正的能階，為一假想能階，但仍是費米-狄拉克分佈為 50% 的區域。於絕對零度時，電子只填在價帶內部。對於半導體而言，能隙較小，非絕對零度時，電子有機會因為熱的緣故而克服能隙分佈到價帶，因此溫度上升時，能夠存在於價帶的電子也越多，半導體的導電性也會上升。但是絕緣體的能隙太大，電子難以分佈到價帶，因此絕緣體不能導電。

參考文獻

1. Conduction band — Wikipedia.http://en.wikipedia.org/wiki/Conduction_band
2. Band theory for solid — Hyperphysics.http://hyperphysics.phy-astr.gsu.edu/hbase/solids/band.html
3. Fermi level — Wikipedia.http://en.wikipedia.org/wiki/Fermi_level
4. Housecroft, C. E. & Sharpe, A. G. (2012). Inorganic Chemistry, 4th edition (pp. 183-185). Pearson Education Limited.