AI的表現好嗎？十種常見的評估指標

AI的表現好嗎？十種常見的評估指標
撰文／陳育婷

有許多方式可以評估一AI是否有效，以分類器為例，常用的指標便有準確率、精確度、召回率等。但是，某項評估指標數值高，就代表分類器表現好嗎？如何正確選擇評估指標，才能真實反映AI效能呢？以下將以常見的二元分類器為例，討論如何藉由資料特性、評估目的及對評估指標的了解，正確選擇合適的評估指標。

常見評估指標

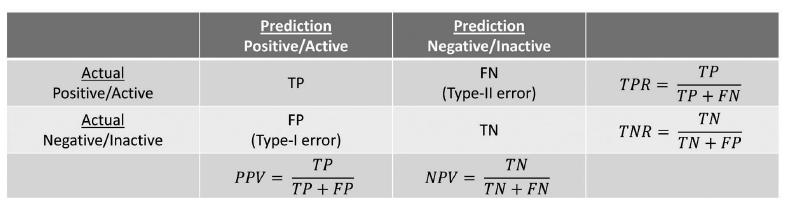
生活中有許多屬於「二元分類」的問題，例如：應該核准或駁回貸款申請？信用卡發卡與否？是否罹患某一疾病？工廠產品是否有瑕疵？涵蓋範圍之廣，跨及各行各業。AI二元分類器的效能，便可藉由分類（預測）結果與實際情形的差距來評估。我們常以混淆矩陣（confusion matrix）列舉可能的情形：

表一、二元分類的混淆矩陣。

上表中，橫列為實際情形，直行為預測結果。「陽性」（positive）代表所關注的類別，如「核准」貸款、「有」罹患疾病；「陰性」（negative）則代表與關注類別相對的另一方。TP（true positive，真陽性）與TN（true negative，真陰性），代表預測結果與實際情形相符的案例；相對的，FP（false positive，偽陽性；又稱第一型誤差，Type I Error）與FN（false negative，偽陰性；又稱第二型誤差，Type II Error），則是預測結果與實際情形不符的情況。由上表便可衍伸出常用的十大評估指標：

• 準確率（Accuracy Rate，ACR）

分類器預測正確的筆數佔所有樣本的比例。這是最常被選用的指標，尤其在沒有特別的關注類別，只是想盡量提升模型預測能力時。公式為：

\[ ACR= \dfrac{TP+TN}{TP+FP+FN+TN(N總樣本個數)} \]

• 真陽性率（True Positive Rate，TPR）& 真陰性率 （True Negative Rate，TNR）

前者衡量陽性類別中被正確預測為陽性的比例，又稱召回率（Recall）；後者則相反，衡量陰性樣本的預測準確率，又稱明確度（Specificity）。若相較於整體準確率，你特別重視陽性樣本的預測好壞，真陽性率會是關鍵。例如：醫生會希望盡量將確實罹病的患者篩選出來（以「確實罹患」為陽性）、銀行希望能降低核准貸款予無償還能力者的可能性（以「無償還能力之人」為陽性）。公式如下：

\[ TPR= \dfrac{TP}{TP+FN}\]

\[TNR= \dfrac{TN}{FP+TN} \]

• 偽陽性率（False Positive Rate，FPR）& 偽陰性率（False Negative Rate，FNR）

與前者相對，此項在評估各類別預測錯誤的比率，與真陽性率與真陰性率有互補關係。前者是評估陰性樣本中被預測為陽性的比率，後者則相反。

\[ FPR= \dfrac{FP}{FP+TN}=1-TNR\]

\[FNR= \dfrac{FN}{TP+FN}=1-TPR \]

• 陽性預測值（Positive Predictive Value，PPV）& 陰性預測值（Negative Predictive Value，NPV）

此兩指標不是以實際類別為分母，而是預測類別，也就是表格中的直行為分母。其中PPV又稱為精確度（Precision），用意在衡量預測陽性的樣本中，有多少比例實際亦為陽性；後者意義相同，但為陰性。

\[ PPV= \dfrac{TP}{TP+FP} \]

\[ NPV= \dfrac{TN}{TN+FN} \]

• F1

目的在衡量真陽性率（TPR）與陽性預測值（PPV）間的平衡。

\[ F1= \dfrac{2 \cdot (PPV \cdot TPR)}{PPV+TPR} \]

此指標只有在TPR與PPV相當（平衡）的情況下才會高；若其中一個表現好，另一個表現極差，F1值則會小很多。例如：當實際陽性與陰性比為10：90時，若僅有1樣本被預測為陽性且預測正確，餘下99個樣本皆預測為陰性（但其中僅90例實際為陰性）。此時PPV=100%， TPR＝10%，F1僅0.18；相較於PPV=50%、TPR=50%的情況（F1=0.5），F1值小很多。

• 幾何平均評估指標 （Geometric Mean，GM）

目的在衡量真陽性率（TPR）與真陰性率（TNR）兩指標間的平衡。

\[ GM=\sqrt{TPR \cdot TNR} \]

當TPR與TNR的值相當且高，GM值會達到高峰；反之，若其中一值高、另一值低，則GM偏低。

• 接收者特徵操作曲線（Receiver Operating characteristic Curve，ROC）& 曲線下方面積（Area Under the Curve，AUC）

通常，分類器會給每個樣本一個分數，分數高代表屬於陽性的機率高，反之則相反。我們可以藉由決定不同的切割點（閾值）來劃分陽性與陰性，不同閾值會有不同的表現；與前述所有指標不同，此指標不限於單一閾值的表現，而是描繪在不同閾值下，偽陽性率（FPR）與真陽性率（TPR）的關係。

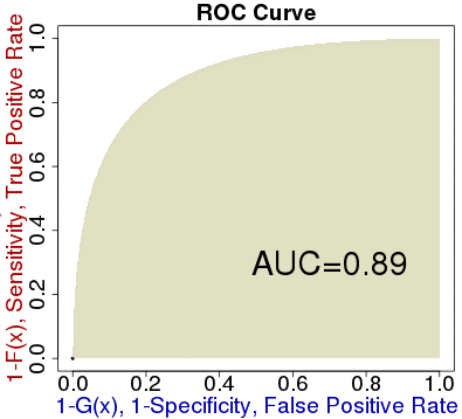
圖二、ROC曲線與AUC示意圖。橫軸為FPR，縱軸為TPR。

圖二中，左下區域代表隨著閾值提高，幾乎沒有樣本被分類為陽性，FPR與TPR皆低；反之，右上區域，隨著閾值降低，幾乎所有樣本都被歸類為陽性，兩指標值皆高。通常我們會用AUC–ROC底下的區塊面積來衡量分類器的好壞：越高代表分類器效果越好。AUC本身也帶有意義，代表：隨機抽取一個陽性樣本Ａ跟陰性樣本Ｂ後，分類器給前者（Ａ）的分數會大於後者（B）分數的機率，所以自然是越高越好。

當資料分布不均

只是，當資料中陽性與陰性案例的比例不均（一般陽性較少，因為會特別關注的通常是如罹病、瑕疵、違約等少數情況），而分類演算法亦未隨之調整，分類器將難以抓住陽性與陰性之間的特徵差異、辨認屬於少數類別的樣本。此外，評估指標的選擇也至關重要，否則可能高（低）估分類器的實際效能，誤導大眾。例如：當95%的資料為陰性時，一律猜測所有樣本皆為陰性，分類器的準確率可達95%；然而，若你關注的類別是陽性，此分類器其實毫無效用。如何改善呢？有以下三個方向。

1. 選擇受資料分布影響較小的評估指標

有些評估指標不受資料類別不平衡的影響，例如ROC-AUC，由於它衡量的是 FPR = P ( Classified = 陽性｜True class = 陰性 ) 以及 TPR = P ( Classified = 陽性｜True class = 陽性 ) 的關係，是已知真實情況下的條件機率，而不是 P(陽性) 及 P(陰性) ，所以在資料類別分布改變時，ROC-AUC並不會改變。另外，因為F1、GM是在最大化兩個不同指標的平衡，雖仍會受到資料分布影響，不過程度相對較小。

2. 調整資料比例

若要讓資料類別分布從不平衡到平衡，也可以直接透過隨機抽樣調整。有兩種抽樣方式，一種針對少數類別做過取樣（oversampling），增加該類別個數；一種則是對多數類別做降取樣（undersampling），目的都是要讓資料陽性與陰性樣本比例為1：1。

3. 調整分類規則

可以透過調整分類閾值的方式，讓陽性樣本較容易被偵測出來。一般的決策閾值是0.5；但是，在不平衡資料情況下，閾值可以更改為「只要陽性樣本的分數高於它在資料中佔的比例（陽性為少數類別的情況中，閾值會小於0.5），就分為陽性」。換言之，假設陰性與陽性的比例為a：b，若​\( P(+|x)> \dfrac{b}{a+b} \)​即判定為陽性，否則為陰性。當然，也可以自行設定成本係數，帶到分類規則中。

正確選擇評估指標

綜合上述可以得知，要正確評估分類器的效能，不能只從單方面切入，還必須同時考量分類目的、對資料的了解以及評估指標的特性。舉例來說，若資料分布不均，則應試圖以上述方法改進分類過程；此外，若你的目的是盡量讓陽性樣本被正確地辨識出來，便應該選擇最能突顯陽性樣本分類效果的真陽性率、精確度、以及衡量兩者平衡的F1等指標；最後，你也必須清楚哪些指標不會受資料分布不均影響，將其列入候選指標。

相反的，我們也不應單憑單一指標的數值妄下結論、誤判系統優劣，而應參酌前述三項條件。此篇僅簡單闡述評估指標間的相關性以及受資料分布影響的程度，在選擇評估指標前，若能閱讀相關論文或網站，對各指標的用意與限制有更多了解，才能避免誤判分類器效能。

參考資料

1. N. Seliya, T. M. Khoshgoftaar, and J. V. Hulse, “A Study on the Relationships of Classifier Performance Metrics,” in 2009 21st IEEE International Conference on Tools with Artificial Intelligence, 2009, pp. 59-66.
2. J. B. Brown, “Classifiers and their Metrics Quantified,” Molecular Informatics, vol. 37, no. 1-2, p. 1700127, 2018.

(本文由教育部補助｢AI報報─AI科普推廣計畫」執行團隊編譯)