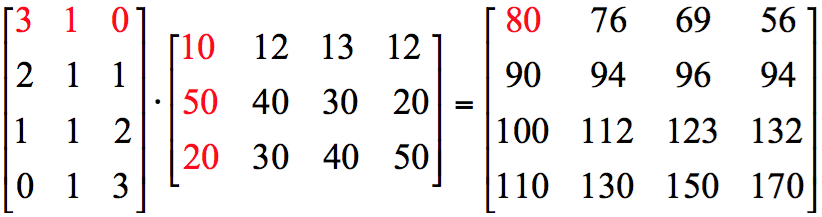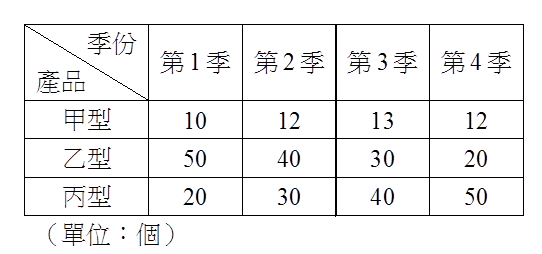線性代數
二階方陣的凱萊─漢米爾頓定理(The Cayley-Hamilton Theorem for 2×2 Matrices)
二階方陣的凱萊─漢米爾頓定理(The Cayley-Hamilton Theorem for 2×2 Matrices)
國立臺南第一高級中學數學科林倉億老師
二次方程式 \(ax^2+bx+c=0\) 求解對我們來說一點都不困難,公式解 \(x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\)
想必不少人都能夠琅琅上口。現在讓我們將方程式的想法,推廣應用到矩陣,會不會有什麼美妙的事情發生呢?直觀來看,若將未知數 \(x\) 看成 \(1\times 1\) 階方陣,結論並沒什麼不同。
但若將未知數 \(x\) 換作其他階的方陣,那結果可就很有趣囉!讓我們先看看二階方陣的例子。
一題有趣的矩陣試題(An Interesting Question of Matrix)
一題有趣的矩陣試題(An Interesting Question of Matrix)
國立臺南第一高級中學數學科林倉億老師
「設 \(A=\begin{bmatrix} 1 &4\\3 & 2\end{bmatrix}\) ,且二階方陣 \(X\)、\(Y\) 滿足 \(X+Y=I\) 且 \(XY=O\),
其中 \(I=\begin{bmatrix} 1 &0\\0 & 1\end{bmatrix}\) 、 \(O=\begin{bmatrix} 0 &0\\0 & 0\end{bmatrix}\) 。若存在實數 \(a>b\) 使得 \(A=aX+bY\),
求 \(a\)、\(b\) 之值。」
上面這個題目曾多次出現在不同的考試之中(敘述略有出入),而無論是哪一份試卷,絕大多數的考生都是被考倒的。以下提供四種不同層次的解法,供讀者參考。
解法一:(努力計算)
\(\begin{cases} X+Y=I\\aX+bY=A\end{cases}\Rightarrow\) 解聯立得 \(\begin{cases} X=\frac{A-bI}{a-b}\\Y=\frac{A-aI}{b-a}\end{cases}\),因為 \(XY=O\),
故 \(\begin{bmatrix} 0 &0\\0 & 0\end{bmatrix}=\displaystyle\frac{1}{-(a-b)^2}\begin{bmatrix} 1-b &4\\3 & 2-b\end{bmatrix}\begin{bmatrix} 1-a & 4\\ 3 & 2-a\end{bmatrix}\Rightarrow b=3-a\)
代入 \((1-b)(1-a)+12=0\Rightarrow a^2-3a-10=0 \Rightarrow (a,b)=(5,-2) or (-2,5)\)
又 \(a>b\) ,故 \((a,b)=(5,-2)\) 。
上述解法就是將 \(X\)、\(Y\) 用 \(A\) 表示後,再利用 \(XY=O\) 解出 \(a\)、\(b\) 。
基本上都是在做計算,看不出此題背後的數學結構為何。
矩陣(Matrix)
矩陣(Matrix)
國立臺南第一高級中學數學科林倉億老師
摘要:本文介紹何謂矩陣及矩陣的相等。
我們經常將許多資料以表格的方式呈現,不僅易於掌握資料,也利於後續的分析。如右表是某家工廠每一季銷售甲、乙、丙三型產品的數量,從表格中我們不僅可以知道每一季的銷售總量,更可以很快地掌握到甲型產品不會受到季節性因素的影響,銷售量大抵上都是10個左右;至於乙、丙型的產品,顯然就與季節性因素有很大的關聯,一個是逐季遞增,另一個恰好相反,是逐季遞減。如果這種銷售趨勢在不同的年度不會有太大的改變,那工廠負責人就可以據此來準備生產所需的零件,甚至是工廠工人的工作時數等等。
矩陣的運算(Operations of Matrices)
矩陣的運算(Operations of Matrices)
國立臺南第一高級中學數學科林倉億老師
摘要:本文介紹矩陣的加法、減法、係數積,以及如何操作矩陣的乘法。
矩陣的加法與減法
當兩個矩陣的列數相等,行數也相等時,我們就稱它們為「同階矩陣」。
例如 $$M = \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right]$$ 與 $$N = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]$$ 同為 $$2\times 3$$ 階矩陣。
同階矩陣我們才能做加法與減法,方法很直觀,就是相同位置的元相加或相減,例如:
$$\begin{array}{ll}M + N &= \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right] + \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{1 + }}1{\rm{0}}}&{{\rm{2 + }}2{\rm{0}}}&{{\rm{3 + }}3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{4 + }}4{\rm{0}}}&{{\rm{5 + }}5{\rm{0}}}&{{\rm{6 + }}6{\rm{0}}} \end{array} \end{array} \right]\\&= \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{1}}}&{2{\rm{2}}}&{3{\rm{3}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{4}}}&{5{\rm{5}}}&{6{\rm{6}}} \end{array} \end{array} \right]\end{array}$$
$$\begin{array}{ll}M – N &= \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right] – \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{1}} – 1{\rm{0}}}&{{\rm{2}} – 2{\rm{0}}}&{{\rm{3}} – 3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{4}} – 4{\rm{0}}}&{{\rm{5}} – 5{\rm{0}}}&{{\rm{6}} – 6{\rm{0}}} \end{array} \end{array} \right] \\&=\left[ \begin{array}{l} \begin{array}{*{20}{c}} {\; – \;{\rm{9}}}&{ – {\rm{18}}}&{ – {\rm{27}}} \end{array}\\ \begin{array}{*{20}{c}} { – {\rm{36}}}&{ – {\rm{4}}5}&{ – {\rm{54}}} \end{array} \end{array} \right]\end{array}$$
用符號來表示就是 $$A = {\left[ {{a_{ij}}} \right]_{m \times n}}$$,$$B = {\left[ {{b_{ij}}} \right]_{m \times n}}$$,
則 $$A+B = {\left[ a_{ij}+b_{ij} \right]_{m \times n}}$$,$$A-B = {\left[ a_{ij}-b_{ij} \right]_{m \times n}}$$。
行列式的故事(The Story of Determinants)
行列式的故事(The Story of Determinants)
國立中央大學數學系單維彰副教授/國立中央大學數學系單維彰副教授
摘要:描述「行列式」的多元歷史,順便藉以闡述,數學並非好似有個明確目標直向前進的發展,而有許多重複和呼應。
當我們由後期的觀點來看數學史或科學史,特別是受限於篇幅和深度的時候,經常營造出一種假象,好像歷代(甚至不同種族、不同地域的)學者們都朝著一個共同而明確的目標前進,有如接力賽似地一棒傳一棒,而造就出今天教科書裡的內容。而真相並非如此。只要能夠多用一點篇幅,並且多引入一些數學內容,就能表現出更多的真相。
矩陣的故事
矩陣的故事 (The Story of Matrices)
國立中央大學數學系單維彰副教授/國立中央大學數學系單維彰副教授責任編輯
摘要:簡介「矩陣」觀念的發生,說明其英文字的緣由,闡述矩陣相乘的意涵。
數學史大約已經認定英國數學家凱萊(Arthur Cayley, 1821-95)是開創矩陣理論的人。凱萊本人卻在文章中指出矩陣之觀念由來已久,而且「matrix」這個字是席維斯(James Sylvester, 1814-97)建議的。正如現在大家所知,矩陣是以矩形排列的一組數。雖說是「矩」陣,但早期的數學家其實僅討論「正方形」矩陣,也就是 \(n\times{n}\) 矩陣或 \(n\) 階方陣,簡稱方陣。
線性方程組的討論(On system of linear equations)
線性方程組的討論(On system of linear equations)
國立新竹高級中學數學科洪誌陽老師/國立臺灣師範大學數學系洪萬生退休教授責任編輯
一般在討論二元一次聯立方程組:
$$(\divideontimes)\left\{\begin{array}{ll}{{a}_{1}{x}+{b}_{1}{y}={c}_{1}}\\{{a}_{2}{x}+{b}_{2}{y}={c}_{2}}\end{array}\right.~~~\mbox{,} {{a}_{i}^2+{b}_{i}^2 \neq 0}~~~\mbox{,} {i}=1\mbox{,} 2$$
其一是利用加減或代入消去法,將原方程式化為:
- 1
- 2