倍角公式(II) (Double-angle Formulas)

倍角公式(II) (Double-angle Formulas)
國立蘭陽女中數學科陳敏晧老師

連結：倍角公式(I)

三角函數中的倍角公式，主要有兩類，一類是二倍角公式，一類是三倍角公式，其中二倍角公式主要有：

1. \(\sin 2\theta= 2\sin \theta \cos \theta\)
2. \(\cos 2\theta= {\cos ^2}\theta- {\sin ^2}\theta= 2{\cos ^2}\theta- 1 = 1 – 2{\sin ^2}\theta\)
3. \(\displaystyle\tan 2\theta= \frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }}\)

這些公式的證明主要是利用正弦與餘弦的和差角公式：

\(\sin \left( {\alpha+ \beta } \right)= \sin \alpha\cos \beta+ \cos \alpha \sin \beta \\\cos \left( {\alpha+ \beta } \right) = \cos \alpha \cos \beta- \sin \alpha \sin \beta\)

若 \(\alpha=\beta=\theta\)，則 \(\sin 2\theta= \sin \theta \cos \theta+ \cos \theta \sin \theta= 2\sin \theta \cos \theta\)，

\(\begin{array}{ll}\cos 2\theta &= \cos \theta \cos \theta- \sin \theta \sin \theta\\&= {\cos ^2}\theta- {\sin ^2}\theta= {\cos ^2}\theta- (1 – {\cos ^2}\theta ) \\&= 2{\cos ^2}\theta- 1 = 2(1- {\sin ^2}\theta ) – 1 = 1 – 2{\sin ^2}\theta\end{array}\)

至於 \(\displaystyle\tan 2\theta= \frac{{\sin 2\theta }}{{\cos 2\theta }}= \frac{{2\sin\theta\cos\theta}}{{{{\cos}^2}\theta- {{\sin }^2}\theta }}= \frac{{2\left( {\frac{{\sin \theta }}{{\cos \theta }}}\right)}}{{1- {{\left( {\frac{{\sin \theta }}{{\cos \theta }}}\right)}^2}}}= \frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }}\)。

而三倍角公式主要有：

1. \(\sin 3\theta=3\sin\theta-4\sin^3\theta\)
2. \(\cos 3\theta=4\cos^3\theta-3\cos\theta\)
3. \(\displaystyle\tan 3\theta=\frac{3\tan\theta-\tan^3\theta}{1-3\tan^2\theta}\)

這些公式的證明主要是利用正弦與餘弦的二倍角公式：

\(\begin{array}{ll}\sin 3\theta&= \sin \left( {2\theta+ \theta } \right) = \sin 2\theta \cos \theta+ \cos 2\theta \sin \theta\\&= \left( {2\sin \theta \cos \theta } \right)\cos \theta+ (1 – 2{\sin ^2}\theta )\sin \theta\\&= 2\sin \theta (1 – {\sin ^2}\theta )+ \sin \theta- 2{\sin ^3}\theta\\&= 3\sin \theta- 4{\sin ^3}\theta\end{array}\)

\(\begin{array}{ll}\cos 3\theta&= \cos \left( {2\theta+ \theta } \right)= \cos 2\theta \cos \theta -\sin 2\theta \sin \theta\\&= \left( {2{{\cos }^2}\theta- 1} \right)\cos \theta- (2\sin \theta \cos \theta )\sin \theta\\&= 2{\cos ^3}\theta- \cos \theta- 2\cos \theta (1 – {\cos ^2}\theta ) \\&= 4{\cos ^3}\theta- 3\cos \theta\end{array}\)

這個公式若以台語發音，會得到一個會心一笑的結果：角三等於四角三減去三角。(其中\(\theta\)不發音)，正弦函數與餘弦函數的三倍角在證明星形線 \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=r^{\frac{2}{3}}\)時派上用場，有興趣的讀者可以自行試試看。

至於正切的三倍角公式則利用正切的和差角公式與二倍角公式推導：

\(\begin{array}{ll}\displaystyle\tan 3\theta&=\displaystyle\tan (2\theta+\theta ) = \frac{{\tan 2\theta+ \tan \theta }}{{1 – \tan 2\theta \tan \theta }}\\&= \frac{\displaystyle{\frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }} + \tan \theta }}{{1 – \left(\displaystyle{\frac{{2\tan \theta }}{\displaystyle{1 – {{\tan }^2}\theta }}} \right)\tan \theta\displaystyle}} =\displaystyle\frac{{3\tan \theta- {{\tan }^3}\theta }}{{1 – 3{{\tan }^2}\theta }}\end{array}\)

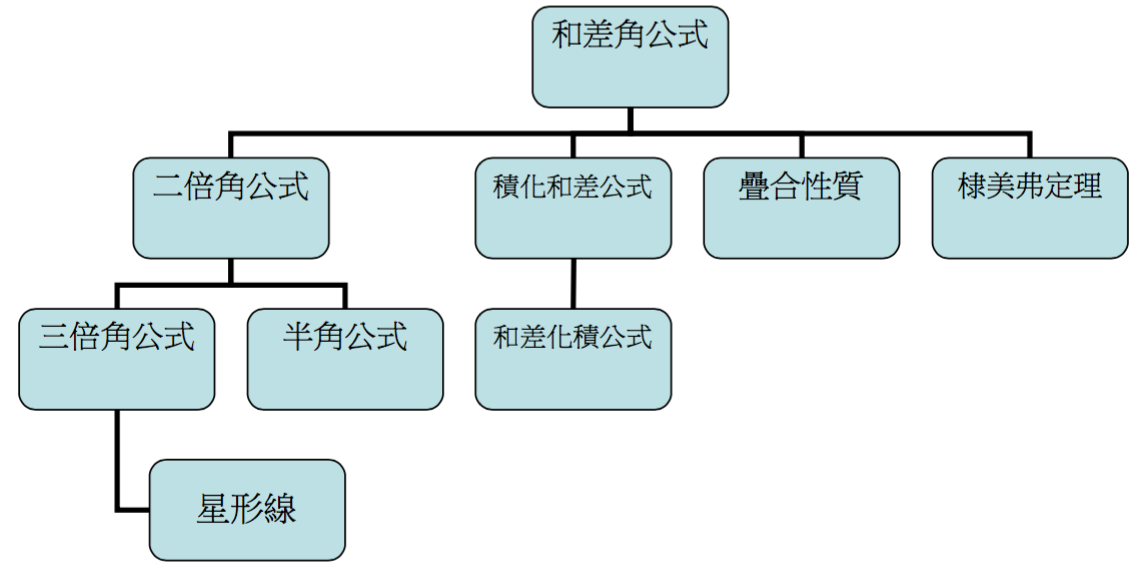
下圖為三角函數公式推論流程圖，可見二倍角公式所處的樞紐地位：

正弦函數與餘弦函數的 \(n\) 倍角公式如下：

\(\sin n\theta= {\cos ^n}\theta- C_2^n{\cos ^{n- 2}}\theta {\sin ^2}\theta+ …\)

\(\cos n\theta= C_1^n{\cos ^{n – 1}}\theta \sin \theta- C_3^n{\cos ^{n – 3}}\theta {\sin ^3}\theta+ …\)

上述的結果比較繁瑣，因此，在教學中可做為有研究精神同學的作業。

至於正切函數的 \(n\) 倍角公式就具有規律性：

\(\tan\theta=\tan\theta\)

\(\displaystyle\tan 2\theta= \frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }} = \frac{{C_1^2\tan \theta }}{{C_0^2 – C_2^2{{\tan }^2}\theta }}\)

\(\displaystyle\tan 4\theta= \frac{{4\tan \theta- 4{{\tan }^3}\theta }}{{1- 6{{\tan }^2}\theta+ {{\tan }^4}\theta }}= \frac{{C_1^4\tan \theta- C_3^4{{\tan }^3}\theta }}{{C_0^4 – C_2^4{{\tan }^2}\theta+ C_4^4{{\tan }^4}\theta }}\)

\(\begin{array}{ll}\displaystyle\tan 5\theta&=\displaystyle \frac{{5\tan \theta- 10{{\tan }^3}\theta+ {{\tan }^5}\theta }}{{1 – 10{{\tan }^2}\theta+ 5{{\tan }^4}\theta }} \\&=\displaystyle \frac{{C_1^5\tan \theta- C_3^5{{\tan }^3}\theta+ C_5^5{{\tan }^5}\theta }}{{C_0^5 – C_2^5{{\tan }^2}\theta+ C_4^5{{\tan }^4}\theta }}\end{array}\)

觀察可得正切函數的 \(n\) 倍角公式：

\(\begin{array}{ll}\tan n\theta &=\displaystyle \frac{{C_1^n\tan \theta- C_3^n{{\tan }^3}\theta+ C_5^n{{\tan }^5}\theta- …}}{{C_0^n – C_2^n{{\tan }^2}\theta+ C_4^n{{\tan }^4}\theta- …}} \\&=\displaystyle \frac{{{\mathop{\rm Im}\nolimits} (\sum\limits_{k = 0} {{i^{2k + 1}}C_{2k + 1}^n{{\tan }^{2k + 1}}\theta } )}}{{{\mathop{\rm Re}\nolimits} (\sum\limits_{k = 0} {{i^{2k}}C_{2k}^n{{\tan }^{2k}}\theta } )}}\end{array}\)

。其中 \(\mathrm{Im}(z)\) 代表複數 \(z\) 的虛部，\(\mathrm{Re}(z)\) 代表複數z的實部。

參考資料：

1. 毛爾(Eli Maor)，鄭惟厚譯，《毛起來說e》，台北：天下遠見出版社，2000。
2. 毛爾(Eli Maor)，胡守仁譯，《毛起來說三角》，台北：天下遠見出版社，2000。
3. 朱建正編撰，《數學問題百則》，台北 : 中央研究院數學研究所，1998，頁48-50。