點到直線的距離公式
點到直線的距離公式 (The Formula of the distance from a point to a line)
臺北市立第一女子中學數學科蘇俊鴻老師
99課綱中將圓與直線的單元放在平面向量之前,進而討論圓與直線的關係時,特別強調運用圓與直線的聯立方程式之解的形態(相等實根、兩相異實根,及沒有實根) 的「代數判定」方法。儘管此法的使用具有一般性,但計算通常較為繁雜。因此,老師通常還會介紹點到直線的距離公式,利用圓心與直線的距離來判斷兩者的關係。
然而,此距離公式的介紹常借助向量方法進行證明,使得許多老師倡議將圓與直線與平面向量兩個單元互換。不過,僅僅為了一個公式的證明大費周章,並且,更動後也涉及平面上直線的向量表示和直線方程式之間的調整問題。本文中提出幾個在99課綱中無須調動次序,也可達到證明點到直線的距離公式之目標的證法。
證法一:(過 \(P\) 點作直線 \(L\) 的垂線,找垂足 \(H\))
如右圖,作 \(\overline{PH}\) 垂直 \(L\) 於 \(H\),
則直線 \(PH\) 方程式為 \(bx-ay=bx_0-ay_0\)
解聯立方程式 \(\left\{ \begin{array}{l} ax + by + c = 0\\ bx – ay = b{x_0} – a{y_0} \end{array} \right.\),
即得 \(\displaystyle H(\frac{{{b^2}{x_0} – ab{y_0} – ac}}{{{a^2} + {b^2}}},\frac{{ – ab{x_0} + {a^2}{y_0} – bc}}{{{a^2} + {b^2}}})\)
進而 \(\begin{array}{ll} d(P,L) &=\displaystyle \overline {PH}= \sqrt {{{({x_0} – \frac{{{b^2}{x_0} – ab{y_0} – ac}}{{{a^2} + {b^2}}})}^2} + {{({y_0} – \frac{{ – ab{x_0} + {a^2}{y_0} – bc}}{{{a^2} + {b^2}}})}^2}}\\&=\displaystyle\sqrt {\frac{{{{(a{x_0} + b{y_0} + c)}^2}}}{{{a^2} + {b^2}}}}= \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
此法概念簡單,直接硬算,但整體過程不算複雜,可鼓勵學生嘗試。
證法二:(若 \(A\) 為直線 \(L\) 上任一點,則 \(\overline{AP}\) 的最小值\(=\)點 \(P\) 到直線 \(L\) 的距離)
令 \(A(x,y)\) 為直線 \(L\) 上任一點,則 \(ax + by + c = 0 \Rightarrow y = \frac{{ – 1}}{b}(ax + c)\)
\(\begin{array}{ll}\displaystyle{\overline {AP} ^2} &=\displaystyle {(x – {x_0})^2} + {(y – {y_0})^2} = {(x – {x_0})^2} + \frac{1}{{{b^2}}}{(ax + c – {y_0})^2} \\&=\displaystyle\frac{1}{{{b^2}}}[({a^2} + {b^2}){x^2} + 2( – {b^2}{x_0} + ab{y_0} + ac)x + {b^2}{x_0}^2 + {(b{y_0} + c)^2}]\end{array}\)
利用二次函數的性質,當 \(\displaystyle x =\frac{{{b^2}{x_0} – ab{y_0} – ac}}{{{a^2} + {b^2}}}\) 時,有最小值。
此時,\(\displaystyle x = \frac{{{b^2}{x_0} – ab{y_0} – ac}}{{{a^2} + {b^2}}}\)
故 \(\begin{array}{ll} d(P,L) &=\displaystyle \sqrt {{{(\frac{{{b^2}{x_0} – ab{y_0} – ac}}{{{a^2} + {b^2}}} – {x_0})}^2} + {{(\frac{{ – ab{x_0} + {a^2}{y_0} – bc}}{{{a^2} + {b^2}}} – {y_0})}^2}} \\&=\displaystyle \sqrt {\frac{{{{(a{x_0} + b{y_0} + c)}^2}}}{{{a^2} + {b^2}}}}=\frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
事實上,發生最小值的 \(A\) 點即為證法一所求出的垂足 \(H\)。利用兩點距離的最小值來求點到直線距離的作法具有一般性,也是空間中解決點到直線距離的主要方法。
證法三:(利用三角形面積)
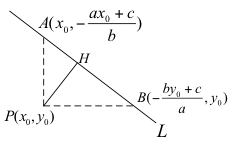
如右圖,過點 \(P(x_0,y_0)\) 分別作鉛直線和水平線交直線 \(L\)
於 \(A({x_0}, – \frac{{a{x_0} + c}}{b})\)、\(B(-\frac{{b{y_0}+c}}{a},{y_0})\)
\(\Delta APB\text{的面積} = \frac{1}{2}\overline {PA}\times \overline {PB}= \frac{1}{2}\overline {AB}\times\overline{PH}\)
又
\(\overline {PA}\displaystyle= \left| {{y_0} – ( – \frac{{a{x_0} + c}}{b})} \right| = \left| {\frac{{a{x_0} + b{y_0} + c}}{b}} \right|\\\overline {PB}\displaystyle= \left| {{x_0} – ( – \frac{{b{y_0} + c}}{a})} \right| = \left| {\frac{{a{x_0} + b{y_0} + c}}{a}} \right|\\\overline {AB}=\displaystyle\sqrt {{{({x_0} + \frac{{b{y_0} + c}}{a})}^2} + {{({y_0} + \frac{{a{x_0} + c}}{b})}^2}}= \sqrt {{a^2} + {b^2}} \left| {\frac{{a{x_0} + b{y_0} + c}}{{ab}}} \right|\)
因此,\(d(P,L)=\displaystyle\overline{PH}=\frac{\overline{PA}\times\overline{PB}}{\overline{AB}}=\frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
利用三角形面積的高來求距離,也是另一種常見的作法。
證法四:(利用三角函數)
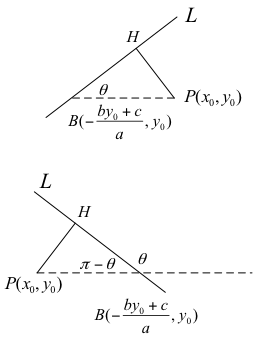
如右圖,過點 \(P(x_0,y_0)\) 作水平線交直線 \(L\) 於
\(\displaystyle B( – \frac{{b{y_0} + c}}{a},{y_0})\) 且 \(L\) 與 \(x\) 軸的正向夾角為 \(\theta\)。
直線 \(L:ax+by+c=0\) 的斜率 \(m=-\frac{a}{b}=\tan\theta\)
則 \(\displaystyle\sin \theta= \sin (\pi-\theta)=\frac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
則 \(\begin{array}{ll}\displaystyle\overline {PH}&=\displaystyle\overline {PB} \sin \theta\\&=\displaystyle \left| {\frac{{a{x_0} + b{y_0} + c}}{a}} \right|\frac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2}} }}\\&=\displaystyle \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
此一證法運用學生剛學過的三角函數,也說明了正切函數 \((\tan\theta)\) 與斜率之間的關係,用來證明點到直線的距離恰到能呼應99課綱的安排,此法最早見於內壢高中林協億老師寫於數學學科中心電子報第60期〈九九課綱中,點到直線距離公式的詮釋〉一文。
上述所提四種證法都能避開向量的使用,同時,所運用的證明概念也具有一般性,老師們在介紹點到直線的距離公式時或可一試!
參考資料:
- 林協億,〈九九課綱中,點到直線距離公式的詮釋〉,數學學科中心電子報第60期(http://mathcenter.ck.tp.edu.tw/Resources/ePaper/Default.aspx?id=60)。
- 郭慶章,〈也談點與直線的距離公式〉。



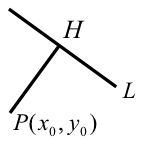
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2)) 

太棒了