半角公式(Half-Angle Formulas)

半角公式(Half-Angle Formulas)
臺北市立第一女子中學數學科蘇俊鴻老師

一般說來，半角公式的推導常是透過倍角公式。由於

\(\cos 2\alpha= {\cos ^2}\alpha- {\sin ^2}\alpha= 2{\cos ^2}\alpha-1=1-2{\sin^2}\alpha\)

因此，

\({\sin^2}\alpha=\frac{{1 – \cos 2\alpha}}{2},{\cos^2}\alpha=\frac{{1+\cos 2\alpha}}{2}\)

令 \(\theta=2\alpha\Rightarrow \alpha=\frac{\theta}{2}\) 代入，即得

\(\sin \frac{\theta }{2} =\pm\sqrt {\frac{{1 -\cos\theta}}{2}} ,\cos\frac{\theta}{2} = \pm\sqrt{\frac{{1 + \cos \theta}}{2}} \)

其中 \(\pm\) 依 \(\frac{\theta}{2}\) 所在的象限決定。至於倍角公式，則是由和角公式推得。
換言之，公式推導的順序是和角公式→倍角公式→半角公式。

然而，當我們檢視托勒密天文學集大成的著作《The Almagest》，他在為製作弦表所提出的一系列命題中，半角公式竟然比和角公式還要更早提出！一起來看看托勒密是如何證明。

如圖一，給定半圓，\(\overline{AC}\) 為直徑，\(D\) 為 \(BC\) 弧的中點。

從 \(D\) 點作 \(\overline{DE}\) 垂直 \(\overline{AC}\) 於點 \(E\)，在 \(\overline{AC}\) 取點 \(F\)，使得 \(\overline{AF}=\overline{AB}\)，

連接 \(\overline{BD}\)，\(\overline{CD}\) 及 \(\overline{DF}\)。

如果令 \(\angle BAC=\theta \)，則 \(\overline{BD}\) 為 \(\theta\) 所對應的弦長，而 \(\overline{CD}\) 為 \(\frac{\theta}{2}\)所對應的弦長。

圖一

首先，\(\overline {CE}= \frac{1}{2}\overline {CF}= \frac{1}{2}(\overline {AC}- \overline{AF}) = \frac{1}{2}(\overline{AC}- \overline{AB})\)，又 \(\Delta ACD\sim\Delta DCE\)，

所以 \(\frac{{\overline {AC}}}{{\overline {CD}}} = \frac{{\overline {CD}}}{{\overline{CE}}} \Rightarrow {\overline {CD}^2} = \overline {AC}\times \overline{CE} \)。

若 \(\overline{AC},\overline{BC}\) 已知，由畢氏定理可得 \(\overline{AB}\)，因而 \(\overline{CE}\) 可知，所以 \(\overline{CD}\) 可求。

進一步，如果令 \(\overline{AC}=1\) ，則 \(\overline{BD}=\sin \theta,\overline{AC}=\cos \theta\)，

那麼 \({\sin ^2}\frac{\theta }{2} = {\overline {CD} ^2} = \frac{1}{2}(1 – \cos \theta ) \Rightarrow \sin \frac{\theta }{2} = \sqrt {\frac{{1 – \cos \theta }}{2}} \)，

就是現在所熟知的半角公式。

事實上，我們也能利用另一個在高中課程中經常出現的問題來證明半角公式。

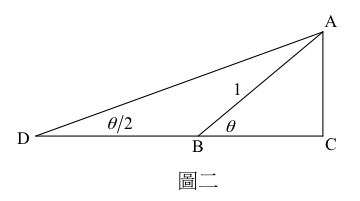
如圖二，給定一直角三角形 \(ABC\)，在 \(\overline{CB}\) 上延長取 \(\overline{BD}=\overline{AB}\)，則 \(\angle ADC = \frac{1}{2}\angle ABC\)。

若 \(\overline{AB}=1\)，\(\angle ABC = \theta \)，則 \(\overline {AC}= \sin \theta,\overline {BC}= \cos \theta\)，

且 \(\begin{array}{ll}\overline {AD}&= \sqrt {{{\sin }^2}\theta+ {{(1 +\cos\theta )}^2}}\\&=\sqrt {{{\sin}^2}\theta+ {{\cos}^2}\theta+ 2\cos\theta+ 1} =\sqrt {2(1 +\cos\theta)}\end{array}\)

因此 \(\sin \frac{\theta }{2} = \frac{{\overline {AC} }}{{\overline {AD} }} = \frac{{\sin \theta }}{{\sqrt {2(1 + \cos \theta )} }} = \frac{{\sqrt {1 – {{\cos }^2}\theta } }}{{\sqrt {2(1+\cos\theta)} }} = \sqrt {\frac{{1 -\cos\theta}}{2}} \)

\(\cos \frac{\theta }{2} = \frac{{\overline {CD} }}{{\overline {AD} }} = \frac{{1 + \cos \theta }}{{\sqrt {2(1 + \cos \theta )} }} = \sqrt {\frac{{1 + \cos \theta }}{2}} \)

換言之，半角公式的證明，除了代數的方法外，亦可運用幾何的方式，有興趣的讀者，不妨自己嘗試看看。