海龍公式的各種證明（上）

Posted on 2011/06/07 in 三角函數, 函數, 數學 with 沒有迴響 14,364 views

海龍公式的各種證明（上）(The Various Proofs of Heron’s FormulaⅠ)
臺北市立第一女子中學數學科蘇俊鴻老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要：本文介紹海龍公式的各種證明。

現行有關高級中學教材的安排，海龍公式出現在三角函數的學習脈絡中，被當成熟練餘弦定律的典範例（以99 課綱來說在高二上學期）。它的證明過程涉及了教師在三角函數教學會強調的知識與技巧。比如：透過平方關係轉換正餘弦；餘弦值與邊長的關係 \((\cos A=\frac{b^2+c^2-a^2}{2bc})\)；乘法公式的使用。

然而，這樣的安排卻也造成對海龍公式認知上的侷限。教師很少進一步討論：海龍公式為何會被提出？在海龍公式中，\(s-a\)，\(s-b\)，\(s-c\) 有什麼幾何意義？有沒有其他證明海龍公式的方法？是否只能在三角函數的脈絡下，介紹及證明海龍公式？

本文中將介紹海龍、梅文鼎 (1633-1721)、李善蘭 (1810 -1882) 及美國羅密士 (E. Loomis, 1811-1889) 等四人的證明，試圖由教學的觀點，說明這些證明中所呈現的特色。就由海龍的原始證明看起。

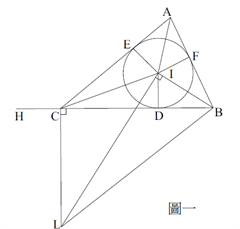
對於西元一世紀的海龍來說，他並沒有今天這樣簡潔有力的符號代數及規則可供其運用，他在《Metric》所提出的證明是純幾何式的。為了便於說明，令 \(\overline{BC}=a\)，\(\overline{AC}=b\)，\(\overline{AB}=c\)。見圖一，下列的幾何性質是海龍是熟悉的：\(\overline{AE}=\overline{AF}=s-a\)，\(\overline{BF}=\overline{BD}=s-b\)，\(\overline{CE}=\overline{CD}=s-c\) 及 \(s=(s-a)+(s-b)+(s-c)\)，其中，\(s=\displaystyle\frac{1}{2} (a+b+c)\)。

證明一開始，便明白地說明他的出發點：由於△ABC面積 \(=\displaystyle\frac{1}{2} (a+b+c)\times r=s \times r\)，其中 \(r\) 是內切圓半徑。因此延伸 \(\overline{CH}=s-a\)，使得 \(\overline{BH}=s\)。

我們只要得出比例式：

\(\displaystyle \frac{s^2}{s(s-a)}=\frac{(s-b)(s-c)}{r^2}\)

接著

\(s^2r^2=s(s-a)(s-b)(s-c)\)

則海龍公式的正確性就大功告成了。

筆者曾在課堂上向學生介紹過此一證明，雖說其證明過程有些關鍵步驟（如相似三角形的選取）很難重現海龍的想法從何而來，但整個證明可以向學生展現其國中所習得之幾何性質的綜合運用，對於學生重新審視與評價所學習到的平面幾何學的相關知識，是有其教學上的價值。

梅文鼎與海龍的出發點相同，先延伸 \(\overline{CH}=s-a\)，使得 \(\overline{BH}=s\)。但不同於海龍，梅文鼎所求出的比例式為：

\(\displaystyle\frac{s-b}{s}=\frac{r^2}{(s-a)(s-c)}\)

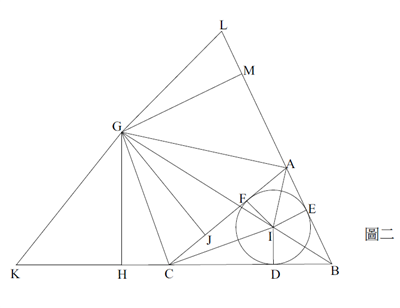
見圖二，梅文鼎用來建立比例式的相似三角形為△BID與△BGH。從教學的觀點來看，這組相似三角形關係的建立是比較容易引導學生觀察。由於相似，可得：

\(\displaystyle\frac{\overline{BD}}{\overline{BH}}=\frac{\overline{ID}}{\overline{GH}}=\frac{\overline{ID}\times\overline{ID}}{\overline{GH}\times\overline{ID}}\)

接著，將 \(\overline{GH}\times\overline{ID}\) 換成 \(\overline{CH}\times\overline{CD}\)，整個證明就告完成。為達此目的，再利用 △CGH 與 △ICD 相似，則：

\(\displaystyle\frac{\overline{GH}}{\overline{CD}}=\frac{\overline{CH}}{\overline{ID}}\Rightarrow\overline{GH}\times\overline{ID}=\overline{CH}\times\overline{CD}\)

然而，如何證明△CGH 與 △ICD 相似呢？這是梅文鼎這個證明最大的挑戰，梅氏透過 △GKC、△GAL 與 △GAC 三者全等，推得 \(\overline{GJ}\) 與 \(\overline{CJ}\) 垂直，進而導出 △CGH 與 △ICD 相似。不過，如何證明 △CGH 與 △ICD 相似，是此證明的困難所在，這也是梅文鼎的圖形比海龍的圖形複雜許多的原因。