海龍公式的各種證明（下）

海龍公式的各種證明（下）(The Various Proofs of Heron’s FormulaⅡ)
臺北市立第一女子中學數學科蘇俊鴻老師/國立臺灣師範大學數學系許志農教授責任編輯

連結：海龍公式的各種證明（上）

摘要：本文介紹海龍公式的各種證明。

接著來看李善蘭在《天算或問》中的證法，主要是論述等式 \((s-a)(s-b(s-c)=sr^2\)，成立。然後兩邊再同乘 \(s\)，即得 \(s^2r^2=s(s-a)(s-b)(s-c)\)。

首先，

李善蘭當然清楚 \(\overline{AE}=\overline{AF}=s-a\)，\(\overline{BF}=\overline{BD}=s-b\)，\(\overline{CE}=\overline{CD}=s-c\)，

這是採取幾何方式論證的必備條件。

不過，李善蘭他卻出人意表地先做出任一邊的高，

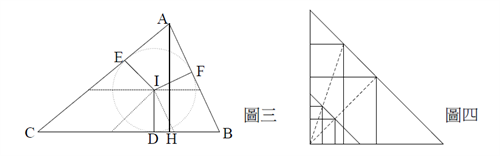
論證比例 \(\displaystyle\frac{\overline{CD}}{{\overline{AC}+\overline{CH}}}=\frac{\overline{BD}}{{\overline{AB}+\overline{BH}}}=\frac{h}{r}\) 的成立 （見圖三），其中 \(\overline{AH}=h\) 為高。

則 \(\displaystyle\frac{\overline{CD}}{{b}+\overline{CH}}\times\frac{\overline{BD}}{{c}+\overline{BH}}=\frac{h^2}{r^2}\)，

又 \(h^2=c^2-\overline{CH}^2=b^2-\overline{BH}^2\Rightarrow (c-\overline{CH})(c+\overline{CH})=(b-\overline{BH})(b+\overline{BH})\)，

且 \(\displaystyle\frac{{c}+\overline{CH}}{{b}-\overline{BH}}=\frac{{b}+\overline{BH}}{{c}-\overline{CH}}=\frac{s}{s-a}\) （見圖四）。

故：

\(\displaystyle \overline{AH}^2=c^2-x^2=b^2-(a-x)^2\Rightarrow x=\frac{c^2+a^2-b^2}{2a}\)

李善蘭的證明讓人印象深刻，他並不是利用這些相關的邊長，設法尋求比例關係。

反倒是將三角形剖分成兩個句股形，利用 \(\overline{AC}+\overline{CH}:\overline{AB}+\overline{BH}=\overline{CD}:\overline{BD}\) 所成的比例關係。此外，李善蘭在比例關係的推導上不像前述海龍與梅文鼎的證明那麼依賴圖形，想要弄懂他們兩人的證明，必須完全掌握證明中所描繪的圖形才行。

反觀李氏的證明中，當他試圖說明比例式 \(\frac{{c}+\overline{CH}}{{b}-\overline{BH}}=\frac{{b}+\overline{BH}}{{c}-\overline{CH}}=\frac{s}{s-a}\) 為何成立時，他所利用的圖形如圖四，與原本用以論述的圖三不同。換言之，對李善蘭而言，比例式 \(\frac{{c}+\overline{CH}}{{b}-\overline{BH}}=\frac{{b}+\overline{BH}}{{c}-\overline{CH}}=\frac{s}{s-a}\) 的成立具有一般性，不侷限在圖三所呈現的三角形而己。

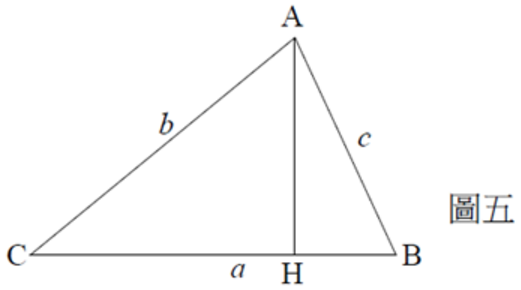
最後，介紹清末曾被教會學校廣泛採用的的數學教科書之一，《八線備旨》一書中的證法（共四卷），此書為美國羅密士  (E. Loomis, 1811-1889) 所著，由傳教士潘慎文 (A. P. Parker, 1850-1924) 翻譯。如圖五，此一證明運用幾何命題：

\(\overline{AC}^2=\overline{AB}^2+\overline{BC}^2-2\overline{BC}\times\overline{BH}\)，推得 \(\displaystyle\overline{BH}=\frac{c^2+a^2-b^2}{2a}\)

再由 \(\displaystyle\overline{AH}^2=\overline{AB}^2-\overline{BH}^2=c^2-\frac{(c^2+a^2-b^2)^2}{4a^2}=\frac{4a^2c^2-(c^2+a^2-b^2)^2}{4a^2}\)

因此，三角形面積 \(=\displaystyle\frac{\overline{BC}\times\overline{AH}}{2}=\frac{1}{4}\sqrt{4a^2c^2-(c^2+a^2-b^2)^2}\)

化簡得海龍公式 \(\sqrt{s(s-a)(s-b)(s-c)}\)，\(\displaystyle s=\frac{1}{2}(a+b+c)\)

事實上，證明所引用的幾何命題 \(\overline{AC}^2=\overline{AB}^2+\overline{BC}^2-\overline{BC}\times\overline{BH}\)

圖五可知，若將 \(\overline{BH}\) 改寫成 \(c\cos B\)，則上述命題即是 \(b^2=a^2+c^2-2ac\cos B\)，

因此，此一命題可以看成是餘弦定律的「幾何版」。不過，我們設 \(\overline{BH}=x\)，由畢氏定理可知：

\(\displaystyle \overline{AH}^2=c^2-x^2=b^2-(a-x)^2\Rightarrow x=\frac{c^2+a^2-b^2}{2a}\)

如果想要向國中生介紹海龍公式的證明，這個證明相當適合在國中實施。

我們由教學觀點去分析海龍公式各個版本證明的特色，並非為了給出一個高低差異的評價，而是為了豐富教師自身的教學內容知識 (PCK)。這也是數學史融入數學教學 (HPM)重要的功能之一。透過各個版本的特色分析，讓教師在教學方法有所比較，也能截長補短。

參考文獻

1. 蘇俊鴻主編 (2006).《海龍公式專輯》，《HPM 通訊》第九卷第四期。可參考 http://math.ntnu.edu.tw/~horng/