平面上點到直線距離（三）

平面上點到直線距離（三） (The distance from a point to a line in the plane Ⅲ）
臺北市立和平高中教師黃俊瑋

連結：平面上點到直線距離（二）

本文承〈平面上點到直線距離(一)〉與〈平面上點到直線距離(二)，繼續提出三類平面上點到直線距離的解法以及相關討論與連結。而本文中的各類解法，主要在直線上任取一點或兩點，造出新向量，所延伸出的方法。

方法5：在直線上任取一點，再利用平行與垂直性質

本類方法主要是引入直線上的一點後，充份利用直線的法向量與方向向量，輔以平行與垂直相關性質與關係，求得投影點與距離。

方法5-1：在直線上任取一點，再利用平行與垂直相關性質

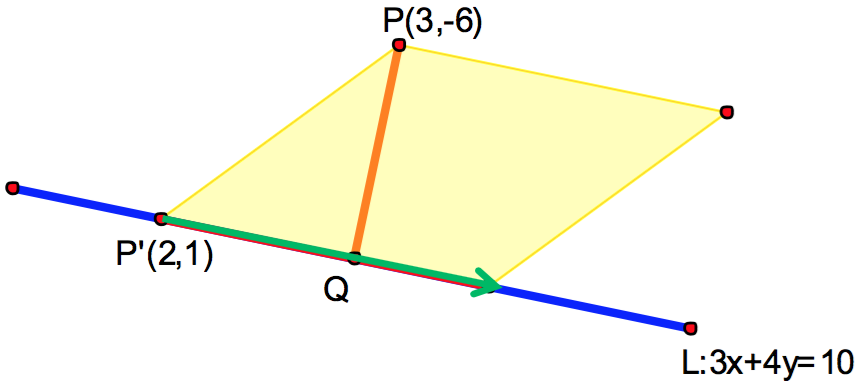
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\) ，
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點，\(\vec{P’Q}\) 與直線之方向向量平行，可設為 \(\vec{P’Q}=t(4,-3)\)。

接下來，可發展出兩種方法，分別利用直線的法向量或方向向量，搭配平行與垂直關係進行解題：

5-1-1

則 \(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 平行直線 \(L:3x+4y=10\) 的法向量
分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\)，可得 \(4(1-4t)=3(-7+3t)\)，解之可得 \(t = 1\)，
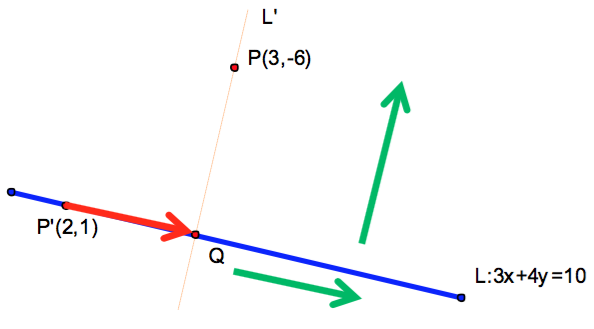
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

5-1-2

\(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 垂直直線 \(L:3x+4y=10\) 的方向向量
內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求(參考圖一所示)。

圖一 在直線上任取一點，再利用平行與垂直性質(一)

方法5-2：在直線上任取一點，再利用平行與垂直相關性質

在 \(L:3x+4y=10\) 上任取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\)，
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點，
\(\vec{PQ}\) 與直線之法向量平行，可設為 \(\vec{PQ}=t(3,4)\)。

接下來，同樣可發展出兩種方法，分別利用直線的方向向量或法向量，搭配平行與垂直關係進行解題：

5-2-1

因為 \(\vec{P’P}+\vec{PQ}=(1+3t,-7+4t)\) 與直線 \(L:3x+4y=10\) 的方向向量平行，
分量成比例 \(\frac{{1 + 3t}}{{ – 7 + 4t}} = \frac{4}{{ – 3}}\)，因此可得 \(4 (-7+4 t) = -3 (1+3t)\)，解之可得 \(t = 1\)，
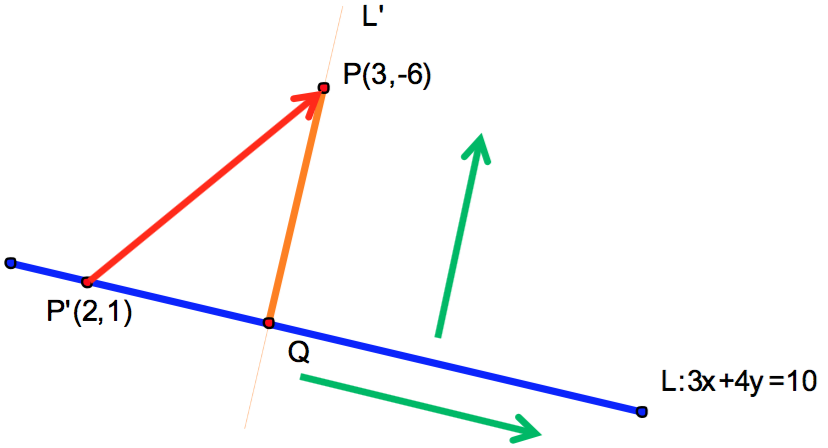
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

5-2-2

\(\vec{P’Q}=\vec{P’P}-\vec{QP}\) 與直線 \(L:3x+4y=10\) 的方向向量垂直，
內積為 \(4(1 – 3t) + ( – 3)( – 7 – 4t) = 0\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\)即為所求。(參考圖二)

評析：以上方法5所需先備知識為《第三冊》第3章－向量的加法、減法、向量平行與垂直之關係、直線的法向量與方向向量。此類方法較方法2來得複雜，相關方法可推廣用於空間中，求點到直線與點到平面距離問題。

圖二 在直線上任取一點，再利用平行與垂直性質(二)

方法6利用向量夾角公式與三角函數

本方法主要是引入直線上一點，造出新向量後，利用與餘弦相關的向量夾角公式來解題。

方法6-1：利用向量夾角公式與正弦

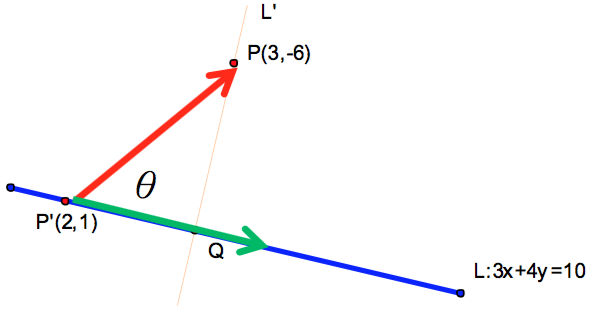
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\)，
\(\vec{P’P}=(1,-7)\) 與直線 \(L\) 方向向量 \((4, -3)\) 之夾角為 \(\theta\)，則 \(\cos\theta=\frac{1}{\sqrt{2}}\)
則 \(\overline {PP’} |\sin \theta | = \sqrt {50} \frac{{25}}{{\sqrt {50}\cdot 5}} = 5\)，即為所求（如圖三所示）。

圖三 利用向量夾角與正弦

方法6-2：利用向量夾角公式與餘弦

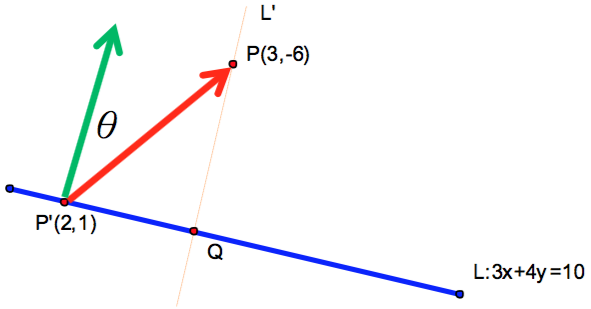
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\)，
\(\vec{P’P}=(1,-7)\) 與直線 \(L\) 法向量 \((3, 4)\) 之夾角為 \(\theta\)，則 \(\cos\theta=\frac{1}{\sqrt{2}}\)
則 \(\overline {PP’} |\cos \theta | = \sqrt {50} \frac{{25}}{{\sqrt {50}\cdot 5}} = 5\)，即為所求（如圖四所示）。

評析：以上方法6所需先備知識為《第三冊》第1章－正弦與餘弦的意義、第3章－兩向量求夾角之餘弦，以及兩向量所張成之三角形面積公式。此方法分別可推廣至空間中，求點到直線距離問題與點到平面距離。但過程中無法求出投影點。

圖四 利用向量夾角與餘弦

方法7：引入一點或兩點利用三角形面積公式

方法7-1：引入一點，利用三角形面積公式或平行四邊形面積公式

在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\)，
又直線的法向量可取 \(\vec{L}=(4,-3)\)，
則，由 \(\vec{P’P}=(1,-7)\) 與 \(\vec{L}=(4,-3)\) 所張平行四邊形面積為 \(|\left| {\begin{array}{*{20}{c}} 4&{ – 3}\\ 1&{ – 7} \end{array}} \right|| = 25\)，
因為平行四邊形的底為 \(|\vec{L}|=5\)，則可求得平行四邊形的高為 \(5\)，即為所求。（如圖五所示）

圖五 引入一點，利用平形四邊形（或三角形）面積公式求高 \(PQ\)

方法7-2：引入兩點，三角形面積公式或平行四邊形面積公式

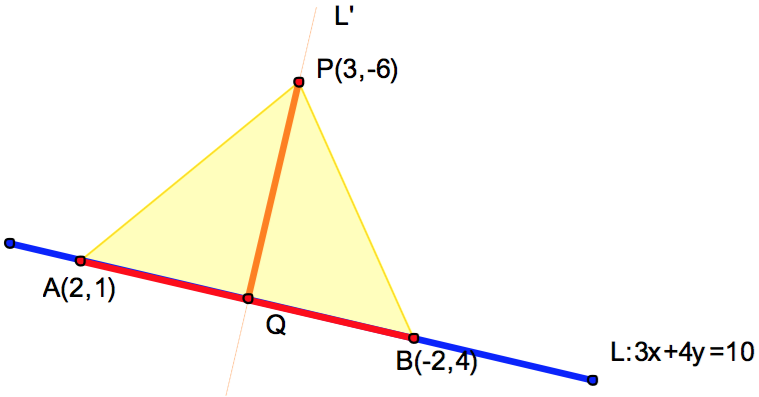
在直線 \(L:3x+4y=10\) 上任取 \(2\) 點 \(A(2,1)\) 與 \(B(-2,4)\)，
可得向量 \(\vec{PA}=(-1,7)\) 與向量 \(\vec{PB}=(-5,10)\)，
這時，可利用各種相關面積公式，計算出三角形 \(PAB\) 的面積為 \(\frac{25}{2}\)。
由於三角形面積等於 \(\frac{1}{2}\cdot\overline{PQ}\cdot\overline{AB}= \frac{1}{2}\cdot\overline{PQ}\cdot 5\)。（如圖六所示）
可求得 \(d(P,L)\) 即為所求距離為 \(5\)。

評析：這個方法所需先備知識為《第三冊》第3章－兩向量所張成之三角形或平行四邊形面積公式。此兩方法皆可推廣至空間中，求點到直線距離問題。但過程中無法求出投影點。

圖六 引入兩點，利用三角形面積公式求高 \(PQ\)

以上，與平面上點到直線距離相關的三篇文章裡，筆者提供了與高中課程相關的多種方法，一方面，供有興趣的讀者趣味一下，同時，也藉此將上述各種解法與想法，與空間中點、線、面求距離問題作一連結。