電磁波的能量

電磁波的能量 (Energy carried by electromagnetic waves)
國立臺灣大學數學系101年高尉庭

在靜電磁學中，我們知道電場與磁場會儲存能量，而單位體積所儲存的能量稱之為「能量密度」(energy density)。在真空中，能量密度與電磁場的關係為：

$$u=\frac{1}{2}(\varepsilon_0E^2+\frac{B^2}{\mu_0})$$

其中 $$u$$ 為能量密度，$$\varepsilon_0$$ ­為真空電容率，$$\mu_0$$ 為真空磁導率。

不過在一般的電磁學下，電磁場不僅能儲存能量，還能夠傳遞能量，而描述電磁場的能量、能量傳遞與帶電粒子做功的關係的定理是坡印廷定理(Poynting’s theorem)。此定理可看成一種在電磁場中的能量守恆的敘述，在數學上與流體力學中所謂的連續方程式(continuity equation)相似。

坡印廷定理：在一封閉曲面 $$S$$ 所圍出的空間 $$V$$ 中，電磁場單位時間對此空間中的電荷所作的總功，加上單位時間中在空間 $$V$$ 電磁場所儲存的能量的變化，會等於能量密度流(坡印廷向量)進入曲面 $$S$$ 的總通量。寫成數學式為：

$$\displaystyle\int_V \vec{J}\cdot \vec{E}\mathrm{d}V+\frac{\partial}{\partial t}\int_V u\mathrm{d}V=\oint_S \vec{S}\cdot \mathrm{d}\vec{a}$$

其中向量 $$J$$ 是電流密度，向量 $$E$$ 為電場，$$u$$ 為能量密度，

向量 $$S$$ 為坡印廷向量(Poynting vector)，在真空中，$$\vec{S}=\frac{1}{\mu_0}\vec{E}\times \vec{B}$$

(註：可能有人會困惑為何電磁場單位時間所作功會是電流密度與電場內積後再積分，
其原因如下：電磁場對此空間中的電荷所作的功，
電磁場對電荷作功所施的力為勞倫茲力 $$\vec{F}=q(\vec{E}+\vec{v}\times \vec{B})$$，
而功率為 $$\frac{\mathrm{d}W}{\mathrm{d}t}=\vec{F}\cdot\vec{v}=(q\vec{v})\cdot\vec{E}$$ ，所以磁場並不會對電荷作功，
故若將電荷表示成電荷密度 $$q\vec{v}\rightarrow \rho\vec{v}\mathrm{d}\tau\rightarrow\vec{J}\mathrm{d}\tau$$ ，則 $$\frac{\mathrm{d}W}{\mathrm{dt}}=\int\vec{J}\cdot\vec{E}\mathrm{d}\tau$$ )

可以注意的是，坡印廷定理的推導只用到了作功的定義、馬克士威方程式與勞倫茲力，所以坡印廷向量是在推導公式的過程中所得到的，其意義仍待進一步詮釋。

不過當我們從物理的角度來看此公式，我們把空間 $$V$$ 中的總力學能設為 $$U_1$$，空間 $$V$$ 中所儲存的電磁場能量設為 $$U_2$$，則此系統的總能量 $$U$$ 就是 $$U_1+U_2$$，所以由坡印廷定理，這空間單位時間能量增加的量，會等於坡印廷向量進入曲面 $$S$$ 的總通量，若我們相信能量守恆是對的，則我們可以把坡印廷向量看成是一種能量密度流(單位時間通過單位面積的能量)，而其向量所指的方向就是能量流的方向，想像成一系統所增加的總能量，就是單位時間有多少能量從(曲面 $$S$$)外面流進來。

圖一 （陳義裕 繪）

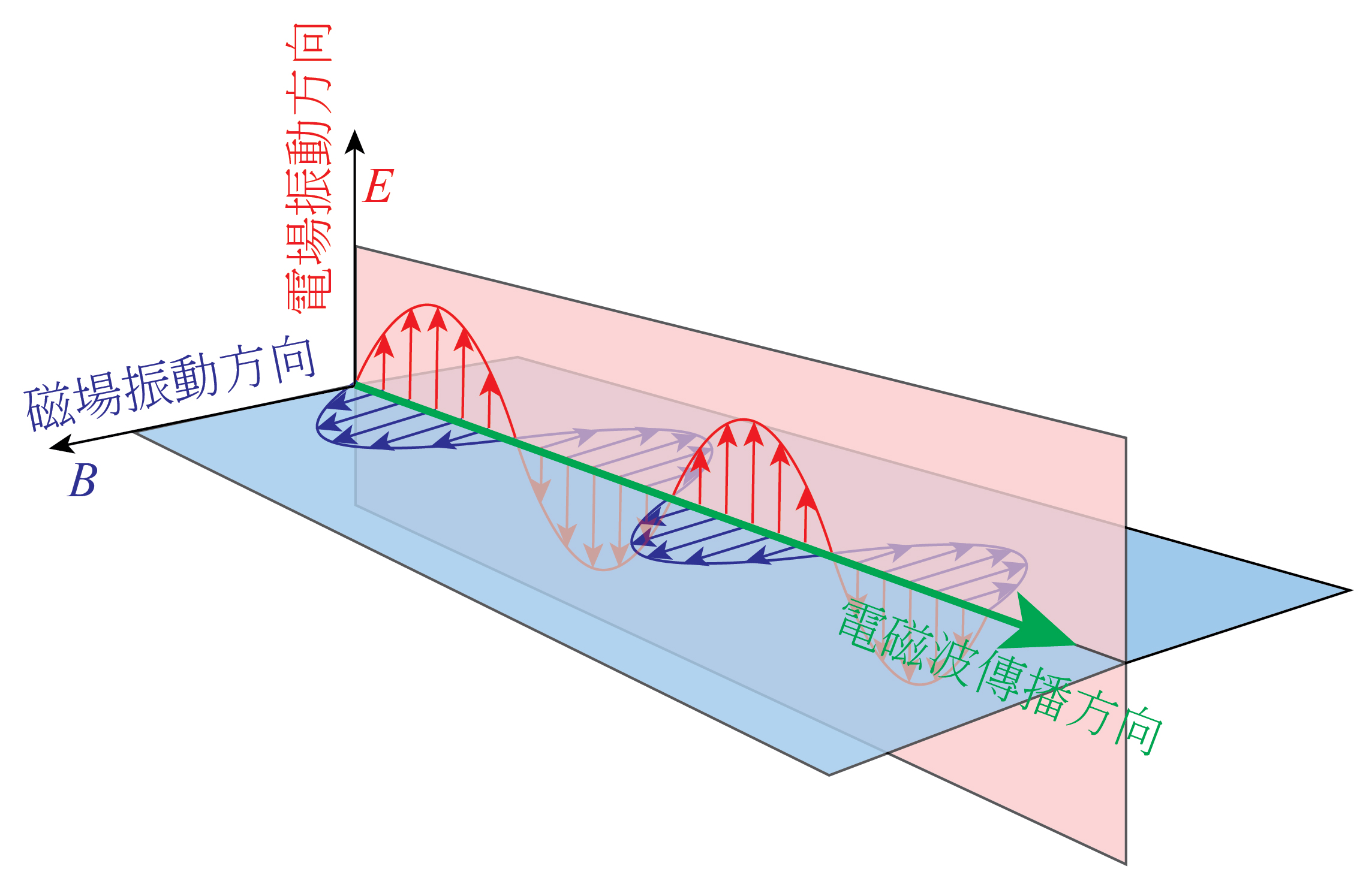
了解坡印廷定理後就能理解為何電磁波可以傳遞能量。先考慮在真空中最簡單的電磁波(圖一)，由上面所述真空中坡印廷向量的公式，我們可以發現坡印廷向量所指的方向，就是電磁波前進的方向，所以我們知道電磁波在前進時會傳送能量。

從另外一個角度去看，我們知道電磁場會儲存能量，所以我們可以預期電磁波中是有儲存能量的，當電磁波以光速 $$c$$ 向前傳遞時，求通過一截面的能量有兩個方式，一個是用坡印廷向量去求，另一個是看多少的能量流通過此截面，當然，這兩種算法所得到的答案是一樣的。

以上述的電磁波為例，設電磁波是往 $$x$$ 軸方向移動，且電磁場大小為

$$E=E_0\sin{(kx-\omega t)},B=E/c$$

則 $$\mathrm{d}t$$ 時間通過 $$x=x_0$$­ 此截面單位面積的能量為

$$\begin{array}{ll} uc\mathrm{d}t&=\epsilon_0cE_0^2\sin^2{(kx_0-\omega t)}\mathrm{d}t\\&=\displaystyle\sqrt{\frac{\epsilon_0}{\mu_0}}E_0^2\sin^2{(kx_0-\omega t)}\mathrm{d}t\end{array}$$

而若用坡印廷向量，$$\mathrm{d}t$$ 時間通過 $$x=x_0$$­ 此截面單位面積的能量為

$$\begin{array}{ll} \left|\vec{S}\right|\mathrm{d}t &=\displaystyle\frac{1}{\mu_0c}E_0^2\sin^2{(kx_0-\omega t)}\mathrm{d}t\\&=\displaystyle\sqrt{\frac{\epsilon_0}{\mu_0}}E_0^2\sin^2{(kx_0-\omega t)}\mathrm{d}t\end{array}$$

從上述可知，兩者所算出來的能量是一樣的。

光是電磁波的一種，因此從生活上，我們也能體會出光是具有能量的，譬如我們能感受到熱輻射，過強的光線會傷害眼睛等。

參考文獻

1. 維基百科. Poynting’s theorem  http://en.wikipedia.org/wiki/Poynting%27s_theorem
2. 維基百科. Poynting vector http://en.wikipedia.org/wiki/Poynting_vector
3. Griffiths, D. J. (1999). Introduction to electrodynamics, 3rd edition. Addison Wesley.