平方關係或畢達哥拉斯三角恆等式 (Pythagorean Trigonometric Identity)

平方關係或畢達哥拉斯三角恆等式 (Pythagorean Trigonometric Identity)
國立蘭陽女中數學科陳敏晧老師

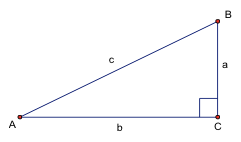
在 \(\Delta ABC\) 中，若 \(\angle ACB=90^\circ\) 且令 \(\theta=\angle BAC\)，如下圖一所示，根據三角函數的定義， 則 \(\sin\theta=\frac{a}{c}\)，\(\cos\theta=\frac{a}{c}\)，\(\tan\theta=\frac{a}{b}\)，\(\cot\theta=\frac{b}{a}\)，\(\sec\theta=\frac{c}{b}\)，\(\csc\theta=\frac{c}{a}\)。

圖一：現行高中數學教科書，銳角三角函數的定義是建立在直角三角形上。

透過直角三角形的畢氏定理關係：\(a^2+b^2=c^2\)，

若將左右兩式同除 \(c^2\)，得 \({\left( {\frac{a}{c}} \right)^2} + {\left( {\frac{b}{c}} \right)^2} = {\left( {\frac{c}{c}} \right)^2}\)，即 \(\sin^2\theta+\cos^2\theta=1\)；

若將畢氏定理關係左右兩式同除 \(b^2\)，得 \({\left( {\frac{a}{b}} \right)^2} + {\left( {\frac{b}{b}} \right)^2} = {\left( {\frac{c}{b}} \right)^2}\)，即 \({\tan ^2}\theta+ 1 = {\sec ^2}\theta\)；

若將畢氏定理關係左右兩式同除 \(a^2\)，得 \({\left( {\frac{a}{a}} \right)^2} + {\left( {\frac{b}{a}} \right)^2} = {\left( {\frac{c}{a}} \right)^2}\)，即 \(1+{\cot^2}\theta= {\csc ^2}\theta\)，

這三個三角函數的恆等式 \(\sin^2\theta+\cos^2\theta=1;\)\({\tan ^2}\theta+ 1 = {\sec ^2}\theta;\)\(1 + {\cot ^2}\theta= {\csc ^2}\theta\) 就是三角函數的平方關係，值得注意的是符號的表徵形式，\((\sin\theta)^2\) 通常以 \(\sin^2\theta\) 表示，而非 \(\sin\theta^2\)。

由於平方關係所產生的理論是根據畢氏定理，因此，三角函數的平方關係又稱為畢達哥拉斯三角恆等式。這三個平方關係是三角函數中最基本的性質，其重要性很類似實數的平方公式：

\({(a + b)^2} = {a^2} + 2ab + {b^2};{(a – b)^2} = {a^2} – 2ab + {b^2}\)

只要熟練這些基本性質，給定任何一個三角函數值，不必根據定義，其餘五個皆可迎刃而解，

例如：已知 \(\sin\theta\) 值， 則 \(\cos\theta=\pm \sqrt {1 – {{\sin }^2}\theta };\)

\(\tan\theta=\pm\displaystyle\frac{{\sin \theta }}{{\sqrt {1 – {{\sin }^2}\theta}}};~~~\)\(\cot\theta=\pm\displaystyle\frac{{\sqrt {1 – {{\sin }^2}\theta } }}{{\sin \theta }};~~~\)

\(\sec\theta=\pm\displaystyle\frac{1}{{\sqrt {1 – {{\sin }^2}\theta } }};~~~\)\(\csc\theta=\displaystyle\frac{1}{{\sin \theta }}\)。

這三個平方關係不論在恆等式的證明或計算方面的運用都極為廣泛，

例如：在三角函數恆等式證明：\(\displaystyle\tan\theta+\cot\theta=\frac{1}{{\sin \theta\cdot\cos\theta }}\)，

就必須借助於第一個平方關係 \(\sin^2\theta+\cos^2\theta=1\)，

即 \(\displaystyle\tan\theta+\cot \theta= \frac{{\sin \theta }}{{\cos \theta }}+\frac{{\cos \theta }}{{\sin \theta }}= \frac{{{{\sin }^2}\theta+ {{\cos }^2}\theta }}{{\sin \theta\cdot \cos \theta }}= \frac{1}{{\sin \theta\cdot \cos\theta}}\)。

第二個恆等式證明例子為 \(\displaystyle\frac{{1+\cot\theta }}{{1 – \cot \theta }}+\frac{{1-\cot\theta }}{{1+\cot \theta }}=- 2\sec 2\theta\)。

此例題除了必須運用第三個平方關係 \(1 + {\cot ^2}\theta= {\csc ^2}\theta\) 外，

還必須引進二倍角公式 \({\cos ^2}\theta- {\sin ^2}\theta= \cos 2\theta\)， 過程如下：

\(\begin{array}{ll}\displaystyle\frac{{1+\cot\theta }}{{1-\cot \theta}}+\frac{{1-\cot \theta }}{{1+\cot\theta }}&=\displaystyle\frac{{{{(1 + \cot \theta )}^2} + {{(1 – \cot \theta )}^2}}}{{(1 – \cot \theta )(1 + \cot \theta )}} = \frac{{2(1 + {{\cot }^2}\theta )}}{{1 – {{\cot }^2}\theta }}\\&=\displaystyle\frac{{2{{\csc }^2}\theta }}{{1 -\displaystyle\frac{{{{\cos }^2}\theta }}{{{{\sin }^2}\theta }}}} \\&=\displaystyle\frac{2}{{{{\sin }^2}\theta- {{\cos}^2}\theta}}=\frac{2}{{-\cos 2\theta }} \\&=- 2\sec 2\theta\end{array}\)

在計算方面，例如化簡 \(2\left( {{{\sin }^6}x+ {{\cos }^6}x} \right)- 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right)\) 式子，如果沒有平方關係的概念， 就無法得出正確答案 \(-1\)。

美國數學競試(American Mathematics Competition, AMC)在1999年第12年級測驗中第15題：

已知 \(x\) 為實數，且 \(\sec x-\tan x=2\) ，則 \(\sec x+\tan x=?\)
\((A)~0.1~~~(B)~0.2~~~(C)~0.3~~~(D)~0.4~~~(E)~0.5\)

解法：這個題目就是在測試考生對於三角函數平方關係的了解程度。

根據平方關係 \({\tan ^2}\theta+ 1 = {\sec ^2}\theta ,\therefore\left( {\sec \theta- \tan \theta } \right)(\sec \theta+ \tan \theta ) = 1\)，

且 \(\sec x-\tan x=2\) ， 則 \(\sec x+\tan x=0.5\)，所以，正確的選項為 \((E)\)。

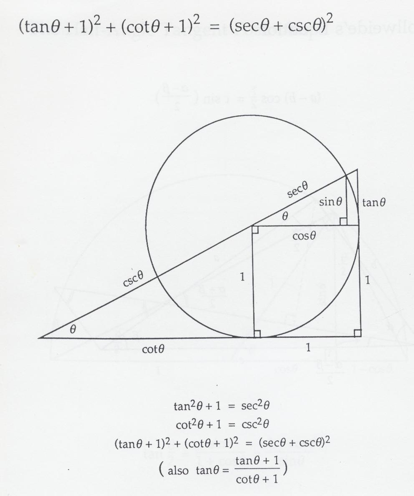
另外，William Romaine在 Proof without Words: Exercise in Visual Thinking 發表有趣的恆等式， 其不言而喻的證明過程中所利用的關係式，即是平方關係的 \(\tan^2\theta+1=\sec^2\theta\) 與 \(1+\cot^2\theta=\csc^2\theta\)。 如圖二所示：

圖二：William Romaine的恆等式

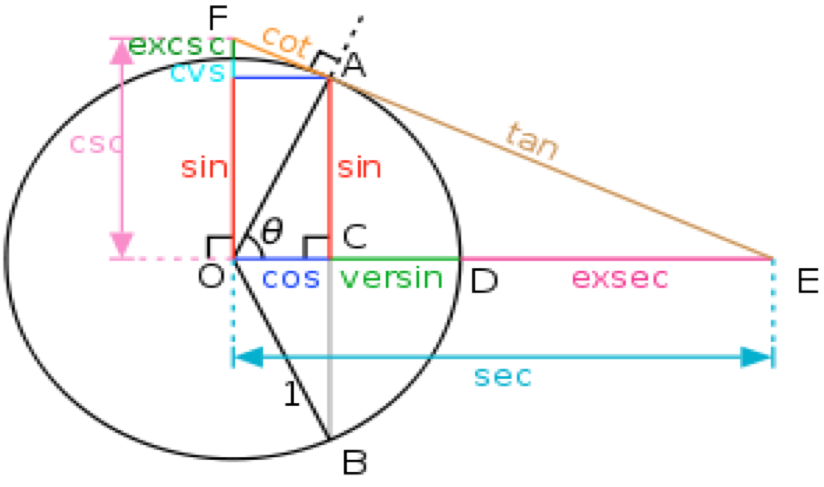
此外，在三角函數的運用範疇中，這些平方關係式除了在有些三角函數需要簡化的時候是很有用外，另一個重要應用 出現在三角函數的積分：一個常用技巧是首先使用三角函數的代換規則，再利用平方關係，即可順利求得積分。

圖三：三角函數平方關係圖

上圖三中的 \(\Delta OAC,\Delta OAE,\Delta OAF\) 蘊含有三個畢達哥拉斯三角恆等式，您是否已經看出端倪呢？

參考資料

1. Roger B. Nelsen (1993). Proof without Words: Exercise in Visual Thinking, Washington D.C.：The Mathematical Association of America, p. 37.
2. http://zh.wikipedia.org/zh-tw/%E4%B8%89%E8%A7%92%E6%81%92%E7%AD%89%E5%BC%8F