另一個重要的無理數：e （Another important irrational number：e）

另一個重要的無理數：e （Another important irrational number：e）
臺北市立和平高中教師黃俊瑋

現今高中一年級課程中的〈數與式〉單元裡，簡單地討論了數系家族中的各個成員。其中，無理數最令一般人感到陌生、無法捉摸。教材中除了介紹諸如 \(\sqrt{n}\) 以及 \(a+\sqrt{b}\) 類的常見無理數外，也介紹了大家熟知的無理數－圓周率 \(\pi\)。

然而，我們也知道，實數線上密密麻麻地佈滿了無窮多個無理數。換句話說，浩瀚的實數世界裡，除了上述常見無理數之外，想必尚有其它忝為人知的成員。除了 \(\pi\) 之外，另一個著名的成員為自然對數的底數 \(e\)。至於 \(e\) 是什麼東東呢？以下我們說分明。

由於 \(e\) 總喜歡藏身自然與生活中，所以我們先來考慮一個與複利有關的問題：假設本金為 \(1\) 單位，並以複利的方式計算。

若利率為 \(100\%\)，那麼 \(1\) 年後本利和為 \((1+1)^1=2\)。

若改成半年支付一次利息，則利率減半為 \(\frac{1}{2}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{2})^2=\frac{9}{4}=2.25\)

若改成四個月支付一次利息，則利率變為 \(\frac{1}{3}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{3})^3=\frac{64}{27}\approx 2.370…\)

若改成三個月支付一次利息，則利率變為 \(\frac{1}{4}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{4})^4=\frac{625}{256}\approx 2.441…\)

\(\cdots\)

以此類推，當利率變成原本的 \(\frac{1}{n}\)，支付次數變成 \(n\) 次，則 \(1\) 年後本利和為：\((1+\frac{1}{n})^n\)

如此，我們可或得一個數列〈\((1+\frac{1}{n})^n\)〉，其中 \(n\) 為自然數。 

計算並觀察數列的前四項後可發現：\(a_1=2,~a_2=2.25,~a_3=2.370…,~a_4=2.441…\)

也許你會猜測，這個數列各項越來越大，但它有可能無止盡地變大增加嗎？

若我們再繼續計算下去，可以發現下列近似值：

\(n\)	10	100	1,000	10,000	100,000	1,000,000
\((1+\frac{1}{n})^n\)	2.59374	2.70481	2.71692	2.71815	2.71827	2.71828

眼尖的讀者可能會發現，它成長「變大」的趨勢越來越緩慢，當 \(n\) 很大時，它幾乎快要「不動」了。接著，讀者可能個然聯想到下一個問題：它是否有上界？再者，更進一步地，它是否收斂呢？若收斂，它的極限值又為何呢？以下，我們分析一些與此數列有關的性質，引出自然對數的底數 \(e\)，最後證明它為無理數。

為了證明此數列的極限值存在，我們引入一個與實數完備性有關常用的判別定理。

定理：設無窮數列 \(<a_n>\) 遞增且有上界，則此數列收斂。

因此，我們需證明：(1)此數列遞增，(2)此數列且有上界。
依據上述定理，即可由這2個結果獲得此數列收斂的結論。

證明：

(1) 此數列遞增

要證明數列遞增，不難想像需要證明它的後項大於等於前項，亦即證明對所有的自然數 \(n\)，皆滿足 \(a_n\le a_{n+1}\)。常用的方法就是「直接比大小」，怎麼比呢？可以拿後項減前項 \(a_{n+1}-a_n\)，並證明其值恆為正或 \(0\)。又或者，拿後項除前項 \(\frac{a_{n+1}}{a_n}\)，並證明其值恆大於等於 \(1\)。

可惜的是，針對 \(<(1+\frac{1}{n})^n>\) 這個數列而言，以這兩種方法並不易行（有興趣的讀者可自行嘗試看看！）。因此，這裡需要新的比法：「間接比大小」。

我們轉個彎，利用二項式定理，分別將 \(a_n\) 與 \(a_{n+1}\) 給「打開」，再作比較。
展開與比較方式如下：

\(\begin{array}{ll}{a_n} &= {(1 + \frac{1}{n})^n} = C_0^n + C_1^n(\frac{1}{n}) + C_2^n{(\frac{1}{n})^2}+\cdots+ C_n^n{(\frac{1}{n})^n}\\&= 1 + n(\frac{1}{n})+\frac{{n(n – 1)}}{{2!}}{(\frac{1}{n})^2}+\frac{{n(n – 1)(n – 2)}}{{3!}}{(\frac{1}{n})^3} +\cdots+ \frac{{n!}}{{n!}}{(\frac{1}{n})^n}\\&= 1 + 1 + \frac{1}{{2!}}(1 – \frac{1}{n}) + \frac{1}{{3!}}(1 – \frac{1}{n})(1 – \frac{2}{n})+\cdots+ \frac{1}{{n!}}(1 – \frac{1}{n})(1 – \frac{2}{n}) \cdots (1 – \frac{{n – 1}}{n})\end{array}\)

\(\begin{array}{ll}{a_{n + 1}} &= {(1 + \frac{1}{{n + 1}})^{n + 1}}\\&= 1 + 1 + \frac{1}{{2!}}(1 – \frac{1}{{n + 1}}) + \frac{1}{{3!}}(1 – \frac{1}{{n + 1}})(1 – \frac{2}{{n + 1}}) +\cdots+ \frac{1}{{n!}}(1 – \frac{1}{{n + 1}})(1 – \frac{2}{{n + 1}}) \cdots (1 – \frac{{n – 1}}{{n + 1}}) + \frac{1}{{(n + 1)!}}(1 – \frac{1}{{n + 1}})(1 – \frac{2}{{n + 1}}) \cdots (1 – \frac{n}{{n + 1}}) \end{array}\)

接著，比較 \(a_n\) 與 \(a_{n+1}\) 前 \(n\) 項，可知：

\(\frac{1}{{k!}}(1 – \frac{1}{k})(1 – \frac{2}{k}) \cdots (1 – \frac{{k – 1}}{k}) \le \frac{1}{{k!}}(1 – \frac{1}{{k + 1}})(1 – \frac{2}{{k + 1}}) \cdots (1 – \frac{{k – 1}}{{k + 1}})\)

，\(\forall k=1,2,…,n\)

尚不然加上 \)a_{n+1}\( 的最後一項，我們即證明了對所有的自然數，\)a_n\le a_{n+1}\(。

(2) 此數列有上界

欲證明此數列有上界即是證明存在某個「夠大的數」，使得數列的每一項都比這個數（上界）它來得小。這裡我們同樣利用上述二項式定理展開後的結果。首先，因為：

\(\begin{array}{ll}{(1 + \frac{1}{n})^n} &= 1 + 1 + \frac{1}{{2!}}(1 – \frac{1}{n}) + \frac{1}{{3!}}(1 – \frac{1}{n})(1 – \frac{2}{n}) +\cdots+ \frac{1}{{n!}}(1 – \frac{1}{n})(1 – \frac{2}{n}) \cdots (1 – \frac{{n – 1}}{n})\end{array}\)

不難看出：\(2 < {(1 + \frac{1}{n})^n} < 2 + \frac{1}{2} + \frac{1}{4} +\cdots+ \frac{1}{{{2^{n – 1}}}} < 3\)

因此，數列 \(<(1+\frac{1}{n})^n>\) 每一項的值的確被限制於 \(3\) 這個數之下。

由(1)與(2)可知數列 \(<(1+\frac{1}{n})^n>\) 遞增且有上界，故其收斂，因此 \(\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\) 存在。於是，我們便把此極限值定為 \(e\)，它亦被稱為自然對數的底數。接著，利用數列 \(<(1+\frac{1}{n})^n>\) 便可計算出其近似值：

\(e = 2.7182818284 59…\)

至於它為何是無理數，稍後作說明。

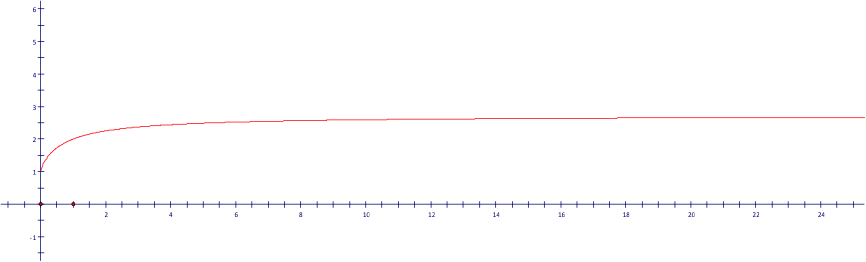
下圖一為函數 \(f(x)=(1+\frac{1}{x})^x\) 的圖形。取 \(x\) 為整數時，便是上述的數列 \(<(1+\frac{1}{n})^n>\)。
從圖中亦可看出隨著 \(x\) 變大，它的函數值也不斷變大，只是一開始上升的速度較快，但慢慢地便開始趨緩了，甚至當 \(x\) 大於 \(10\) 之後，從圖形看起來已接近水平線了。從圖中也可以發現，函數的值皆在 \(2\) 與 \(3\) 之間。

本文一開始，我們從複利的例子得到了數列 \(<(1+\frac{1}{n})^n>\)，
並證明了它遞增且有上界，\(\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\) 存在，並把此極限值定為 \(e\)。
另一方面，讀者可能會在某些書中發現，我們也會把「\(e\)」定義成：

\({\rm{e}}=\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}= \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} + \frac{1}{{4!}} +\cdots+ \frac{1}{{n!}} +\cdots\)

看到這裡，讀者可能會好奇，究竟這是怎麼一回事？不是說 \(e\) 是無理數嗎？怎麼它可以寫成一長串有理數之和？這裡，我們進一步分析無窮級數 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\) 相關性質。首先，我們同樣證明它收斂，接著，證明它恰等於前面提到的 \(\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\)，並證明它為無理數。

收斂性證明如下：

考慮由前 \(n\) 項和形成的數列 \(<\sum\limits_{k = 0}^n {\frac{1}{{k!}}} >\)，\(n=1,2,3,…\)

(1)因為原數列各項皆正，因此，數列 \(<\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}>\) 顯然遞增。

(2)再者，\(\begin{array}{ll}\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}&= \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} + \frac{1}{{4!}} + \frac{1}{{5!}} +\cdots\\&\le 1 + \frac{1}{1} + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}} +\cdots= 1 + \frac{1}{{1 – {\textstyle{1 \over 2}}}} = 3\end{array}\)

由(1)(2)以及前文提到的收斂判別定理
可知 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}= \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots\frac{1}{{n!}} +\cdots\)的極限值存在。

至於怎麼證明 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\) 與 \(\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\) 相等呢？

只要能分別證明 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\le \mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\) 以及 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\ge \mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\)，

即能證明 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\) 與 \(\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\) 相等。

首先，我們先證 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\ge \mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}\)。

我們拿\(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\) 前 \(n\) 項和所形成的數列 \(<\sum\limits_{k = 0}^n {\frac{1}{{k!}}}>\) 與無窮數列 \(<{(1 + \frac{1}{n})^n}>\) 作比較。

同樣利用二項展式定理，展開整理後可得：

\(\begin{array}{ll}{(1 + \frac{1}{n})^n} &= C_0^n + C_1^n(\frac{1}{n}) + C_2^n{(\frac{1}{n})^2} +\cdots+ C_n^n{(\frac{1}{n})^n}\\&=1 + n(\frac{1}{n}) + \frac{{n(n – 1)}}{{2!}}{(\frac{1}{n})^2} + \frac{{n(n – 1)(n – 2)}}{{3!}}{(\frac{1}{n})^3} +\cdots+ \frac{{n!}}{{n!}}{(\frac{1}{n})^n}\\&\le 1 + 1 + \frac{{{n^2}}}{{2!}}{(\frac{1}{n})^2} + \frac{{{n^3}}}{{3!}}{(\frac{1}{n})^3} + \frac{{{n^4}}}{{3!}}{(\frac{1}{n})^4} +\cdots+ \frac{{{n^n}}}{{n!}}{(\frac{1}{n})^n}\\&=1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\end{array}\)

即 \({(1 + \frac{1}{n})^n}\le\sum\limits_{k = 0}^n{\frac{1}{{k!}}}\)

另一方面，我們也可證明 \(\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}\le\mathop {\lim }\limits_{n\to\infty }{(1 + \frac{1}{n})^n}\)，這部份的證明留作習題，留待讀者自行嘗試。

綜合上述結果，由於 \({(1 + \frac{1}{n})^n}\le\sum\limits_{k=0}^n {\frac{1}{{k!}}}\) 且 \(\mathop {\lim }\limits_{n\to\infty}{(1 + \frac{1}{n})^n}\ge\sum\limits_{k=0}^n {\frac{1}{{k!}}}\)，可推得：

\(\mathop {\lim }\limits_{n \to \infty }{(1 +\frac{1}{n})^n}=\sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}= 1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}}+\cdots\)

因此，可得：

\({\rm{e}} =\mathop {\lim }\limits_{n \to \infty }{(1 + \frac{1}{n})^n} = 1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\)

證明了上述結果後，我們便可用之證明 \(e\) 為無理數。回想高中教材（第一冊的附錄）中，證明 \(\sqrt{2}\) 為無理數時，利用了歸謬證法。依此靈感與經驗，這裡我們同樣利用歸謬證法來證明 \(e\) 為無理數。

證明：

首先，假設 \({\rm{e}} = 1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\) 為有理數，

令其為 \(\frac{p}{q}\)，其中 \(p\) 與 \(q\) 皆為互質的正整數。

由 \(\frac{p}{q} = \sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}= 1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\)

可知：\(0 < \frac{p}{q} – (1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{q!}}) \le \frac{1}{{(q + 1)!}}[1 + \frac{1}{{q + 1}} + {(\frac{1}{{q + 1}})^2} +\cdots] = \frac{1}{{(q + 1)!}}\frac{{q + 1}}{q} = \frac{1}{{q \cdot q!}}\)

同乘以 \(q{!}\) 可得：\(0 < q![\frac{p}{q} – (1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{q!}})] \le q!\frac{1}{{q \cdot q!}} = \frac{1}{q} < 1\)

然而，\(q![\frac{p}{q} – (1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{q!}})] \\= q!(\frac{p}{q}) – q!(1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{q!}})\)

其中，\(q{!}(\frac{p}{q})\) 與 \(q!(1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{q!}})\) 皆為自然數。

但是，並不存在介於 \(0\) 與 \(1\) 之間的自然數，因此導致了矛盾。而造成此矛盾的原因，是因為我們假設 \(e\) 為有理數，於是 \(e\) 當為無理數才是，證明完成！

綜合本文內容，我們提出幾個與 \(e\) 有關的結論：

1. \({\rm{e}} = \sum\limits_{k = 0}^\infty{\frac{1}{{k!}}}= \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\)。
2. \({\rm{e}} = \mathop {\lim }\limits_{n \to \infty }{(1 + \frac{1}{n})^n}\)。
3. \(e\) 為無理數。
4.  \(2<e<3\)。

除了上述範圍外，實際上我們也可利用數列 \(<{(1 + \frac{1}{n})^n}>\)
或利用 \(1 + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} +\cdots+ \frac{1}{{n!}} +\cdots\) 來計算其近似值：

\(e = 2.718281828459…\)

此即為圓周率之外，另一個重要的無理數。其小數點後的數字無窮無盡，不循環亦無規律，藏身大自然。以其所造出的指數函數 \(e^x\) 亦為常見且重要的函數。