伯努力試驗與二項分布
伯努力試驗與二項分布 (Bernoulli Trial and Binomial Distribution)
國立成功大學統計系/東吳大學財務工程與精算數學系專任統計助教 杜柏毅
在生活中,有很多的事情都只有兩種結果 (outcome),例如考試是否及格、明天是否下雨、丟擲銅板並觀察其結果。當一個試驗只有兩種可能結果(成功與失敗),且兩個結果出現之機率為固定(若成功機率為 \(p\),則失敗機率為 \(1-p\)),我們稱這樣的試驗為伯努力試驗 (Bernoulli trial)。當我們重複進行多次相同的伯努力試驗(如丟擲一相同硬幣數次),且已知這些試驗之間的結果互相獨立(即這次試驗的結果不影響下次試驗的結果),則稱為二項實驗 (binomial experiment)。
舉例來說,本季罰球命中率約為九成的 NBA 球星 Stephen Curry 連罰 \(3\) 球(對運動員來說,連罰 \(3\) 球並不會有體力上的耗損)即是一個實驗次數為 \(3\),成功機率為 \(0.9\) 的二項實驗。若我們觀察這個二項實驗中成功的次數,則稱此成功次數為一個符合二項分配 (binomial distribution) 的隨機變數,以“\(+\)”代表進球,“\(-\)”表示未進球,其可能的結果以隨機變數及其發生的機率以表一所示:
表一、Stephen Curry 連罰 3 球的結果、隨機變數及其發生的機率。
| 結果 S | 隨機變數 X:三次罰球的總進球數 x | 機率 f(x) |
| +++ | x = 3 | \(0.9^3\) |
| ++- +-+ -++ |
x = 2 | \(C^3_20.9^2(1-0.9)^1\) |
| +-- -+- --+ |
x = 1 | \(C^3_10.9^1(1-0.9)^2\) |
| --- | x = 0 | \(0.1^3\) |
表一中第一欄的結果為隨機實驗的樣本空間(定義為 \(S\)),而第二欄隨機變數的結果則是透過一個隨機變數(定義為 \(X\)),將樣本空間的結果轉換由實數 \(\{x: 0,~1,~2,~3\}\)。第三欄表述隨機變數的結果之發生機率(記為 \(f(x)\),\(f\) 為機率函數)。觀察進球數 \(x\) 與發生機率 \(f(x)\) 的關係,我們可將不同進球數的機率,以一個函數表達:
\(f(x)=C^3_x0.9^x(1-0.9)^{3-x},~~~~~~x=0,~1,~2,~3\)
此時我們可以說隨機變數 \(X\) 屬於「實驗次數 \(n = 3\),成功機率 \(p = 0.9\) 的二項分配」,記為
\(X\sim B(3,0.9)\)
若推廣至實驗次數為 \(n\),成功機率為 \(p\),則機率分配為
\(f(x)=C^n_xp^x(1-p)^{n-x},~~~~~~x=0,~1,…,~n\)
若有一隨機變數 \(X\) 屬於此分配,則記為
\(X\sim B(n,p)\)
接著,我們要討論二項分配的平均數(代表分配的集中趨勢)與變異數(代表分配的離散程度)。若有一隨機變數 \(X\sim B(n,p)\),我們可將 \(X\) 視為 \(n\) 個成功機率為 \(p\),且互相獨立的白努力分配 \((X_i\sim B(1,p))\) 的總和。
\(X=X_1+X_2+…+X_n\)
透過期望值的運算,可以得知其中任何一個伯努力分配的平均數為
\(E(X_i)=\sum\limits^1_{x=0}xp^x(1-p)^{1-x}=p\)
變異數為
\(Var(X_i)=E(X^2_i)-[E(X)]^2=\sum\limits^1_{x=0}x^2p^2(1-p)^{1-x}-p^2=p(1-p)\)
由於原隨機變數 \(X\) 中的所有 \(X_i\) 均為互相獨立的隨機變數,基於期望值與變異數的可加性,我們可知原隨機變數 \(X\) 的平均值與變異數為
\(E(X)=E(X_1+X_2+…+X_n)=E(X_1)+E(X_2)+…+E(X_n)=np\)
\(Var(X)=Var(X_1+X_2+…+X_n)=Var(X_1)+Var(X_2)+…+Var(X_n)=np(1-p)\)
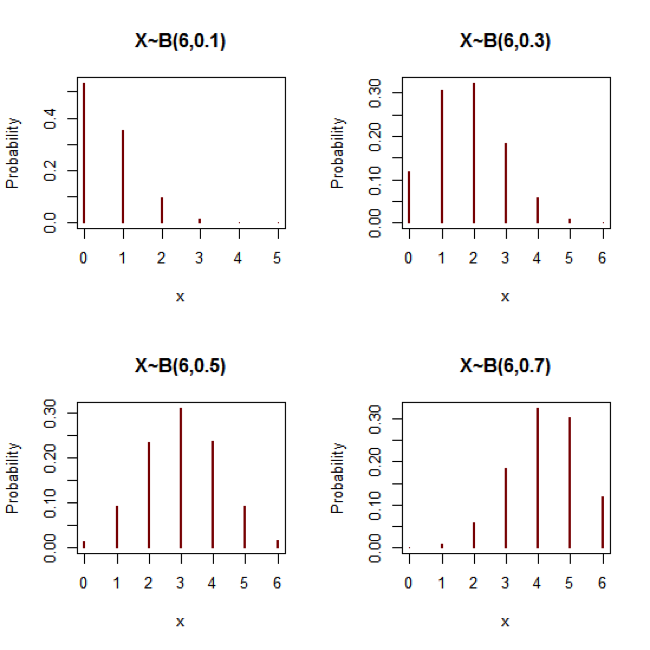
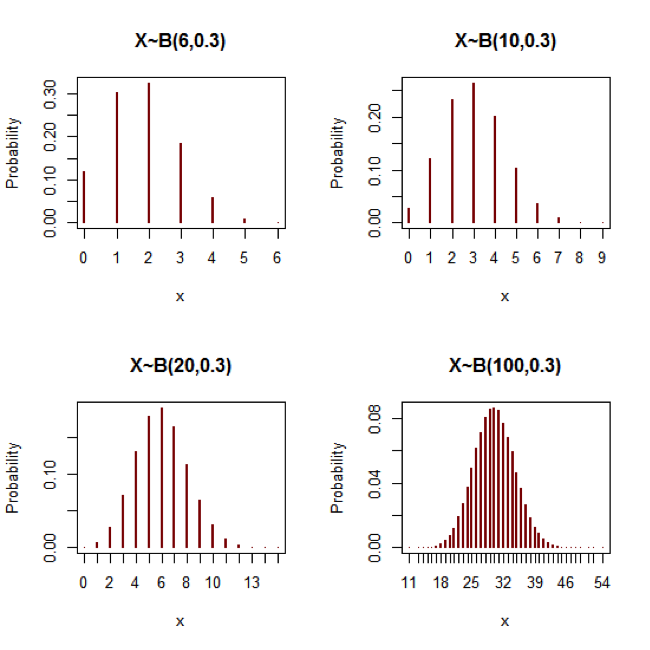
二項分配在不同實驗次數,及不同成功機率的分配圖形如圖一和圖二。
另外,二項分配之所以被稱為二項分配,是因為分配的機率值是二項式定理的二項係數。二項式定理與二項分配之機率總和:
二項式定理:\(\sum\limits^n_{x=0}C^n_xa^xb^{n-x}=(a+b)^n\)
二項分配之機率總和:\(\sum\limits^n_{x=0}f(x)=C^n_xp^x(1-p)^{n-x}=[p+(1-p)]^n=1\)
參考文獻
- Hogg, R. V., & Craig, A. T. (1970). introduction to mathematical statistics. 7th Ed. p.11
- Hogg, R. V., Tanis, E., & Zimmerman, D. (2014). Probability and statistical inference. 9th Ed. p.49


 前一篇文章
前一篇文章 下一篇文章
下一篇文章 海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題 
