四方連塊的正方形拼圖遊戲

四方連塊的正方形拼圖遊戲 (The Puzzle of Tetrominoes)
國立臺中女中數學科賴信志老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要：多方塊的矩形拼圖（Tiling the rectangle）是一個有趣而常見的拼圖遊戲，它的基本規則是：每一種等面積的多方連塊至少都用一個來拼一個矩形。「四方連 塊」（tetrominoes）是指四個單位正方形以邊與邊相連接而成，並扣除圖形旋轉、鏡射，所形成之五種不同形狀的幾何平面圖形。本文探討四方連塊的 拼圖問題。

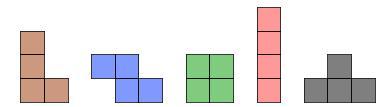
多方塊的矩形拼圖（Tiling the rectangle）是一個有趣而常見的拼圖遊戲，它的基本規則是：每一種等面積的多方連塊至少都用一個來拼一個矩形。「四方連塊」（tetrominoes）是指四個單位正方形以邊與邊相連接而成，並扣除圖形旋轉、鏡射，所形成之五種不同形狀的幾何平面圖形，如下圖所示，分別為 L 型、Z 型、O 型、I 型、T 型。

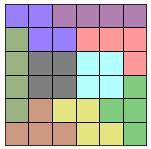
在四方連塊的拼圖遊戲中，我們已經知道：若每個四方連塊恰用一個並無法拼出一個面積為 $$20$$ 單位的矩形；若是每種四方連塊恰用二個，我們可以拼出 $$5\times 8$$ 和 $$4\times 10$$ 的矩形。然而能否拼出恰用 $$9$$ 個四方連塊組成最小可能的 $$6\times 6$$ 正方形？這個問題的答案顯然是肯定的，只要嚐試著動手拼拼看，應該馬上可以得到很多種不同的拼法，下圖為 O 型、I 型、T 型、Z 型 各 $$2$$ 個和 $$1$$ 個 L 型的例子：

幾次嚐試之後，我們一直無法拼出一個最極端狀況的拼法，也就是：是否能用 $$5$$ 個同一型的四方連塊和其他四型的四方連塊各 $$1$$ 個來拼成 $$6\times 6$$ 正方形？這個問題的解答可以藉由一個拼多方塊常用的手法加以解決，首先將 $$6\times 6$$ 正方形塗成黑白相間的棋盤（如下圖），

而將這五個類型的四方連塊放在此棋盤上時， L 型、Z 型、O 型、I 型恰各覆蓋 $$2$$ 黑格和 $$2$$ 白格，但 T 型只可能覆蓋 $$1$$ 黑格、$$3$$ 白格或是 $$3$$ 黑格、$$1$$ 白格，由於 $$6\times 6$$ 正方形棋盤上黑、白格數相同，所以若要能將此棋盤蓋滿，T 型四方連塊的個數必需為偶數，因此不可能用 $$5$$ 個同一型的四方連塊和其他四型的四方連塊各 $$1$$ 個來拼成 $$6\times 6$$ 正方形。藉此我們也可以知道這個拼圖遊戲中的 T 型個數只可能是 $$4$$ 個或 $$2$$ 個。

在諸多四方連塊拼成 $$6\times 6$$ 正方形的方法中，我們可以發現有一些拼法可以將 $$6\times 6$$ 正方形分割成兩個較小的矩形，下圖為其中一個例子（$$6\times 4$$、$$6\times 2$$）：
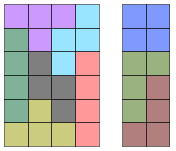在這個例子中，可以透過將 $$6\times 4$$ 和 $$6\times 2$$ 矩形旋轉 $$180^\circ$$、水平及鉛直鏡射來重新組合成 $$6\times 6$$ 的正方形，扣除組合成大正方形後本身圖形可由旋轉、鏡射變換而成的相同圖形，共可組合出 $$8$$ 種不同拼法。所以當我們進一步想求出用四方連塊拼出  $$6\times 6$$ 正方形的所有可能拼法數時，可把可能的拼法分成兩類，一類的拼法是可以將 $$6\times 6$$ 正方形拆成更小的兩個矩形，另一類則是不行。若要將 $$6\times 6$$ 的正方形拆成兩個矩形，這兩個小矩形的面積必定是 $$4$$ 的倍數，故只可
能拆成 $$6\times 4$$、$$6\times 2$$（或 $$6\times 2$$、$$6\times 4$$）兩個矩形，而 $$6\times 2$$ 的矩形的拼法只有如下 $$4$$ 種（將旋轉、鏡射後相同的圖形視為同一種）：

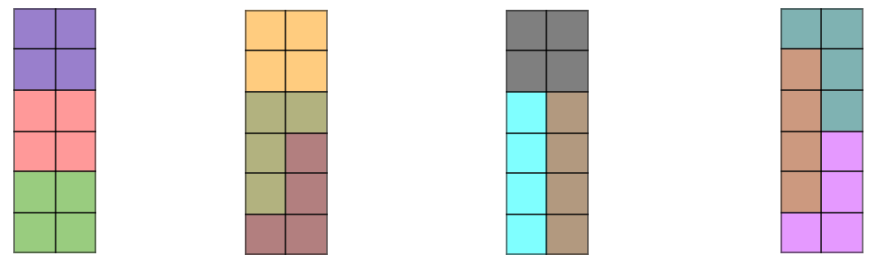由左至右分別為：$$3$$ 個 O 型、$$1$$ 個 O 型 $$2$$ 個 L 型、$$1$$ 個 O 型 $$2$$ 個 I 型、$$1$$ 個 I 型 $$2$$ 個 L 型

上面的 $$4$$ 種 $$6\times 2$$ 的矩形中皆不含 T 型和 Z 型，所以 $$6\times 4$$ 的矩形可依包含的四方連塊種類分成：只含 T,Z, L 型、T,Z,I 型、T,Z,O 型、T,Z,L,I 型、T,Z,L,O 型、T,Z,I ,O 型及T,Z,I,O,L 型；而這七個種類不一定都會存在，經檢驗可知只含 T,Z,O 和只含 T,Z,I,O 的 $$6\times 4$$ 矩形是不可能存在的，而在剩下 $$5$$ 種 $$6\times 4$$ 矩形中，有一些又可再拆成兩個更小的矩形，討論可能的拆法有：拆成  $$5\times 4$$ 和 $$1\times 4$$、$$4\times 4$$ 和 $$2\times 4$$、$$3\times 4$$ 和 $$3\times 4$$，在需要含 T 型和 Z 型的條件下，可構成小矩形的種類並不多，讀者可以試著把所有的可能情況找出來。利用拆成更小矩形的方式可以更有效率地計算可能的拼圖方式，例如下圖由 $$2\times 4$$、$$4\times 4$$ 和 $$6\times 2$$ 矩形組合出 $$6\times 6$$ 正方形：

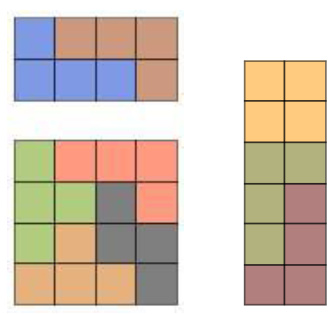因為 $$2\times 4$$ 矩形有原圖形及水平鏡射兩種圖形，$$4\times 4$$ 矩形有原圖形及水平鏡射的圖形並皆可再旋轉 $$90^\circ$$、$$180^\circ$$、$$270^\circ$$，所以可組合出 $$2\times 2\times 4=16$$ 種不同的 $$6\times 4$$ 矩形，又這 $$16$$ 個矩形除了原圖形，皆可旋轉 $$180^\circ$$ 或作鉛直鏡射，加上 $$6\times 2$$ 矩形有原圖形和旋轉 $$180^\circ$$ 的圖形，故有 $$16\times 3\times 2 = 96$$ 種不同方式組合出 $$6\times 6$$ 正方形。要計算以四方連塊（每種類型至少一個）組成 $$6\times 6$$ 正方形拼圖方式的方法數，並不是一件容易的事，不過我們應該可以利用上敘的分類方式，加上「人工檢驗」或利用電腦檢驗，進一步把拼出 $$6\times 6$$ 正方形的方法數計算出來。

參考資料

1. http://en.wikipedia.org/wiki/Tetromino
2. S. W. Golomb, Checker Boards and Polyominoes, The American Mathematical Monthly, Vol. 61,No. 10（Dec., 1954）, pp. 675-682.
3. 潮音國小，天旋地轉難成矩，連塊方略破謎局，中華民國第四十七屆中小學科學展覽會作品說明書