１的ｎ次方根（nth root of 1）

１的ｎ次方根（nth root of 1）
國立屏東高級中學數學科楊瓊茹老師/國立臺灣師範大學數學系洪萬生教授責任編輯

在一元 $$n$$ 次方程式中，首先討論最簡單且重要的方程式 $$x^n=1$$，它顯然有 $$1$$ 這一個實根。根據代數基本定理與因式定理得知，$$n$$ 次多項式方程式恰有 $$n$$ 個複數根，所以方程式 $$x^n=1$$ 共有 $$n$$ 個根。現在，我們應用棣美弗定理求解出 $$n$$ 個 $$1$$ 的 $$n$$ 次方根。

假設複數 $$z$$ 是方程式 $$x^n=1$$ 的根，即 $$z^n=1$$。
以極式表示，$$z=r(\cos\theta+i{\sin}\theta)$$，$$1=1(\cos{0}+i{\sin}0)$$，
代入 $$z^n=1$$ 得 $$[r^n(\cos\theta+i{\sin}\theta)]=1(\cos{0}+i{\sin}0)$$。
由棣美弗定理 $$[r^n(\cos{n}\theta+i{\sin}n{\theta})]=1(\cos{0}+i{\sin}0)$$
由複數相等性質（$$r$$ 是大於 $$0$$ 的實數，$$n\theta$$ 和角度 $$0$$ 是同界角）

雖然整數 $$k$$ 有無限多個，乍看之下好像也有無限多個 $$\theta$$，

但 $$k=0,1,2,\mbox{…},n-1$$ 得出的 $$n$$ 個輻角 $$\theta$$，

和 $$k=n,n+1,n+2,\mbox{…},2n-1$$ 得出的 $$n$$ 個輻角 $$\theta$$ 是同界角，

而且 $$\sin\theta$$、$$\cos\theta$$ 的週期為 $$2\pi$$，

故取 $$k=0,1,2,\mbox{…},n-1$$，即複數 $$z$$ 的主輻角 $$\theta$$ 為 $$0,\frac{2\pi}{n},\frac{4\pi}{n},\mbox{…}\mbox{…},\frac{2(n-1)\pi}{n}$$。

因此，$$1$$ 的 $$n$$ 個 $$n$$ 次方根為

$$\displaystyle z_k=\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n},~k=0,1,2,……,n-1$$

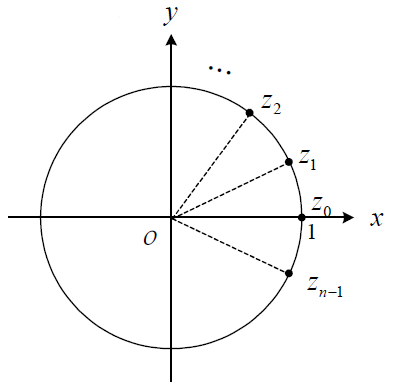
由於 $$|z_k|=1$$，所以在複數平面上，$$n$$ 個根所代表的 $$n$$ 個點都在單位圓上，並且平均分布在單位圓的內接正 $$n$$ 邊形的頂點上，角度間隔 $$\frac{2\pi}{n}$$，如下圖。

底下，分別以 $$1$$ 的 $$3$$ 次方根、$$4$$ 次方根、$$5$$ 次方根與例說明。

如此漂亮的 $$n$$ 個根及其圖形應用棣美弗定理便可解出，但是，許多學生對於 $$1$$ 有 $$n$$ 個相異的 $$n$$ 次方根，總是覺得困惑和驚訝，而且看到根竟然是複數更感到瞠目結舌。其實，在棣美弗所處的時代，專業的數學家對複數無理根或是把複數納入三角函數形式也會大感訝異。